1. Паняцце метрычнай прасторы+

Кажуць, што на непустым неаднаэлементарным мностве Х зададзена метрыка p, калі кожным 2 яго элем. x і y пастаулены у адпаведнасць неадмоуны лік p(x;y) і пры гэтым выконваюцца умовы (аксіемы метрыкі)

1. p(x;y)=0  x=y (аксіема рэфлексіўнасці )

2.p(x;y)=p(y;x) 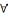x,y 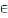Х(аксіема сіметрычнасці)

3.p(x,y)≤p(x,z)+p(z,y), x,y,z Х (аксіема трохвугольніка)

Метрычнай прасторай наз. усякае мноства Х, на якім уведзена метрыка p . Такім чынам метрычная прастора – гэта пара (X,p) . Элемент. мноства X наз. пунктамі метрычнай прасторай (X,p), іх абазн. літарамі : x,y,z,…,a,b,c,… .Лік p(x,y) наз. адлегласцю паміж пунктамі x і y. Мн-ва X наз. носьбітам метрычнай прасторы (X,p).

Прыклад. 1 Няхай X=R –м.п. p ,p(x,y)=|x-y| пакажам, што p-метрыка на Х. Па-першае: p: RxR →R⁺(т.к. |x-y|≥0 , x,y R Па-другое: выконваецца усе 3 аксіемы метрыкі:1 p(x,y)=0 г.зн. |x-y|=0  x-y =0  x-y;2 p(x,y)=|x-y|=|y-x|=p(y,x) x,y R;3 p(x,y)=|x-y|=|x-z|+|z+y|≤|x-z|+|z-y|=p(x;z)+p(z;y) x,y,z R .такім чынам p-метрыка на мн-ве R.

2. Шары і сферы метр. Прасторы. Абмежаваныя мн-вы.

Няхай (X,p) абстрактная м.п., а X, r R⁺ , яе падмн-ва B(a,r)={xЄX |p(x,a)<r} наз. адкрытым шарам у гэтай пр-ры з цэнтрам у пункце a і радыуса r. D(a,r)={xЄX |p(x,a)≤r} наз. замкнутым шарам. S(a,r)={xЄX |p(x,a)=r}- наз. сферай . Адкрыты і замкнуты шары B(a,r) і D(a,r) часта наз. адкрытым і адпаведна замкнутым r-наваколлямі пункта а у пр-ры (X,p) . Шары і сферы у пр-ры Rⁿ атрымалі абазн.: Bⁿ(a,r) , Dⁿ(a,r), Sⁿ(a,r)

Прыклад. (n=2) R² a=(a₁,a₂), r>0

B²(a,r)={(x₁,x₂)| p((x₁,x₂),a)<r}={(x₁,x₂) | <r}

D²(a,r)= {(x₁,x₂) | ≤r}

S(a,r)={(x₁,x₂) | =r}

Дыяметрам падмноства А метрычнай прасторы (X,p) наз. лік diamA=inf p(x,y), т.е. ніжняя грань мн-ва.

Падмн-ва А м.п. (X,p) наз. абмежаваным, калі яго дыяметр канцоуны лік (diam< +∞)

Сцв. Падмн-ва м.п. з’яул. абмежаваным, калі існуе шар у гэтай пр-ры , у якім цалкам змяшчаецца дадзенае мн-ва .

3.Індуцыраваная метрыка . Падпрастора метрычнай прасторы

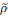
Калі дамовіцца адлегласць паміж пунктамі падмн-ва А м.п. (X,p) вылічваць па той формуле , па якой вылічваецца адлегласць паміж гэтымі пунктамі як пунктамі м.п. (X,p) атрымаем метрыку на падмн-ве А, якая наз. індуцыраванай метрыкай p м.п. (X,p) . Больш дакладна індуцыраванай метрыкай на падмн-ве А яе п. (X,p) наз. адлюстраванне : 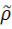=p|_AxA : AxA →R⁺ , (x,y)=p(x,y) .

Сцв. Індуцыраваная метрыка 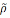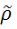з'яул. метрыкай на падмн-ве А.

Сцв.Падмн-ва А тапалаг. пр-ры (X,p) на яком зафіксаваны індуцыраваная метрыка 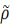наз. падпр-рай м.п. (X,p)

Прыклад Няхай X=RxR, p –эуклідава метрыка г.з. (X,p)=R², А=S¹ X . Разгледзім 2 метрыкі на S¹

d: d(x,y)=|xy| -даужыня xy. S : S(x,y)=|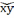 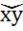| - даужыня найкарацейшай дугі . Метрыка d з'яул. індуцыраванай метрыкай на S' , а метрыка S –не (яна з'яул. унутранай метрыкай на S')

(S¹ ,d)- гэта падпр-ра пр-ры R²

(S²,S) – м.п. , але не пр-ра R²

4. Адкрытыя мн-вы . Натуральныя тапалогіі метрычнай прасторы. Пункт X пад-ва А м.п. (X,p) наз. унутраным пунктам мн-ва А, калі існуе яго наваколле w(X,r) , якое цалкам змяшчаецца у мн-ве A(w(x,r)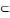 А)

r- наваколле w(х,r) пункта х гэта ці адкрыты шар B(x,r) ці замкнуты D(x,r) . Падмн-ва А м.п. (X,p) наз. адкрытым у ей , калі кожны яго пункт з'яул. унутраным

Прыклад. Шар B²(a,r) – адкрытае мн-ва у R². На самой справе адвольны яго пункт Х мае наваколле B²(X,r-p(x,a)) якое цалкам змяшчаецца у ім . Шар D²(a,г) і сфера S'(a,г) – не з'яул. адкрытымі мн-вамі у R².

Заувага Мн-ва можа быць адкрытым у адной пр-ры, але не адкрытым у другой. Такім чынам паняцце адкрытага мн-ва залежыць ад метрыкі пр-ры . Напрыклад: шар B²(a,r)- адкрытае у R² , але не адкрытае у R³.

Тэарэма (характар. ул-ці сукупнасці адкрытых мн-в) Сукупнасць τ усіх адкрытых у пр-ры (X,p) мн-вау задавальняе наступным умовам :

1) Ø, Х τ ;

2) аб'яднанне адвольнай колькасці мн-вау з сукупнасці τ належаць τ ; 3)перасячэнне канцоунай колькасці мн-ау з τ належаць τ.

Доказ. 1. Відавочна (па азначэнню)

2. Разгледзім аб'яднанне 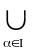A_α , дзе A_α Єτ , αЄ I (I – індэкснае мн-ва адвольнай магутнасці ) Няхай х – адвольны пункт гэтага аб'яднання , тады х прінад. А_α0 , α₀ Є I . A_α0 Єτ , існуе наваколле w(x,г) , якое цалкам змяншаецца у мн-ве А_α0 , тады w(x,г) с 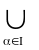A_α , а г. Зн. Х – унутраны пункт гэтага аб'яднання

3. Разгледзім перасячэнне 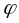, дзе А_i –мн-ва сукупнасці τ , i=1,n . Няхай х –адвольны пункт з гэтага перасячэння , г.зн. х прінад. А_i , i=1,n . Паколькі A_iЄτ , г. зн. існуе наваколле w(x,n) , якое цалкам змяшчаецца у А_i . Т.к. 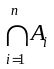усе гэтыя наваколлі канцэнтравальныя (з адзіным цэнтрам у х) і іх канцоуныя колькасці існуе наіменьшае з іх , якое змяшчаецца ва усіх астатніх : Няхай г₀=min {г₁,…,г_n}, тады наваколле w(x,г₀) цалкам змяшчаецца у , гэта значыць х – унутраны пункт перасячэння.

Сукупнасць τ усіх адкрытых у метрыч. пр-ры мн-ваў наз.натуральнай тапалогіяй гэтай пр-ры.