
- •2. Элементарная крывая. Агульныя крывыя. Простыя крывыя.
- •5. Гадкая (рэгулярная) элементарная крывая.
- •10. Датычная прамая крывой.
- •11. Нармаль плоскай крывой. Нармальная плос-касць прасторавай крывой. Вугал паміж крывымі.
- •12. Даўжыня дугі крывой. Формулы для вылічэння даўжыні дугі.
- •15. Суправаджальны трохграннік. Кананічны базіс.
- •17. Крывізна і кручэнне.
- •20. Крывізна і кручэнне акружнасці, гарфіка функцыі, шрубавай лініі.
- •21. Крывая нулявой крывізны. Пункты спрамлення (выпроствання).
- •22. Крывая нулявога кручэння. Пункты сплашчэння.
- •23. Натуральныя раўнанні. Асноўная тэарэма тэорыі крывых.
- •27. Элементарная паверхня (э.П.). Агульная павер-хня (а.П.). Простая паверхня (п.П.).
- •29. Гладкая (рэгулярная) элементарная паверхня.
- •35. Датычная плоскасць паверхні.
- •36. Нармаль паверхні. Кананічны базіс.
- •37. Першая квадратычная форма параметрызава-най паверхні. Запіс першай квадратычнай формы ва унутраных каардынатах. Дыскрымінант першай ква-дратычнай формы.
- •38. Вылічэне даўжыні дугі крывой на паверхні.
- •39. Вылічэнне вугла паміж крывымі на паверхні.
- •40. Вылічэнне плошчы абсягу на паверхні.
- •41. Другая квадратычная форма параметрызава-най паверхні.
23. Натуральныя раўнанні. Асноўная тэарэма тэорыі крывых.
Азн.:
залежнасці
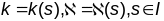 ад натуральнага па-раметра s
пункта крывой называецца натуральным
раўнаннем гэтай прамой.
ад натуральнага па-раметра s
пункта крывой называецца натуральным
раўнаннем гэтай прамой.
Прыклады натуральных раўнанняў:
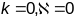
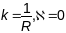 – акружнасць
радыцса R.
– акружнасць
радыцса R.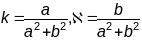
Тэарэма:
(асноўная
тэарэма тэорыі крывых) няхай зададзены
две адвольныя непарыўныя функцыі
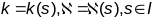 ,
прычым
,
прычым
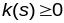 .
Тады існуе адзін, з дакладнасцю да
палажэння у прасторы крывая
.
Тады існуе адзін, з дакладнасцю да
палажэння у прасторы крывая
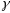 ,
для якой пры адпаведным выбары яе
натуральнай параметрызацыі натуральныя
раўнанні будуць мець выгляд
,
для якой пры адпаведным выбары яе
натуральнай параметрызацыі натуральныя
раўнанні будуць мець выгляд
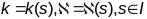 ,
г.зн.
,
г.зн.
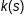 - функцыя крывізны,
- функцыя крывізны,
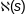 - функцыя кручэння.
- функцыя кручэння.
Прыклады ўжывання гэтай тэарэмы:
1.
Усякая плоская крывая, пастаяннай не
нулявой крывізны, з’яўляуцца акружнасцю,
ці яе часткай. Натуральные раўнанні
гэтай крывой будуць мець выгляд
 (паколькі крывая плоская). Гэта натуральныя
раўнанні акружнасці
(паколькі крывая плоская). Гэта натуральныя
раўнанні акружнасці
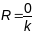 (ці яе часткі) паколькі для акружнасці
маем
(ці яе часткі) паколькі для акружнасці
маем
 .
Паколькі натуральнае раўнанне адпа-веднае
тэарэме, вызначае крывую адназначна з
даклад-насцю да руху ў прасторы і
адвольная іншая плоская крывая з
крывізной
.
Паколькі натуральнае раўнанне адпа-веднае
тэарэме, вызначае крывую адназначна з
даклад-насцю да руху ў прасторы і
адвольная іншая плоская крывая з
крывізной
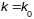 таксама будзе акружнасцю з
таксама будзе акружнасцю з
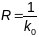 ці яе часткай.
ці яе часткай.
2.
Усякая прасторавая крывая з пастаяннымі
ненулявымі крывізной і кручэннем,
з’яўляюцца шрубавай лініяй, ці яе
часткай. Натуральные раўнанні такой
крывой будуць мець выгляд
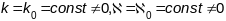 .
З другога боку гэта будуць натуральныя
раўнанні шрубавай лініі
.
З другога боку гэта будуць натуральныя
раўнанні шрубавай лініі
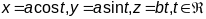 ,
дзе
,
дзе
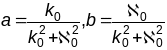 .
.
Праверым
гэта:
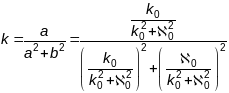 ,
,
 .
Паколькі крывая вызначаецца адназначна
(з дакладнасцю да руху), то крывая, ў якой
.
Паколькі крывая вызначаецца адназначна
(з дакладнасцю да руху), то крывая, ў якой
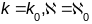 будзе шрубавай лініяй ці яе часткай.
будзе шрубавай лініяй ці яе часткай.
27. Элементарная паверхня (э.П.). Агульная павер-хня (а.П.). Простая паверхня (п.П.).
Э.п.
у прасторы гэта гамеаморфны вобраз у
гэтай прасторы элементарнага двумернага
прамежка (г.зн. адкрытага ці замкнутага
круга, замкнутай паўакружнасці ці ўсей
плоскасці) ці адвольнага падмноства
плоскасці, гамеаморфнага прамежку.
Абазнач.
Прыклады э.п.:

Прыклады не э.п.

А.п.
у прасторы гэта фігура, якую можна
пакрыць канечным ці злічоным мноствам
э.п. Абазнач.
Вынік: вывучэнне а.п. у малым зводзіцца да вывучэння э.п.
Тапалагічна звычайным пунктам а.п. называецца такі яе пункт, які мае наваколле у прасторы (г.зн. адкрыты шар з цэнтрам у гэтым пункце), перасячэнне якога з паверхняй з’яўляецца э.п. Пры гэтым магчымы два выпадкі:
1) калі ўказаннае перасячэнне гамеаморфна, тады звычайны пункт наз. унутранным;
2) калі гэтае перасячэнне гамеаморфна замкнутай плоскасці, то пункт называецца краявым.
Прыклады:
1. Кожны пункт гранічнай акружнасці замкнутай паўсферы краявы, астатнія – унутранныя.
Пункт а.п., які не з’яўляецца тапалагічна звычайным, называецца тапалагічна асаблівым.
А.п. наз. простай, калі яна , па-першае, з’яуляецца звязнай і, па-другое, не мае тапалагічна асаблівых пунктаў, усе яе пункты тапалагічна звычайныя.
Прыклады:
1. Усе э.п.
2. Сфера.
3.Шар.
4. Паверхня піраміды.
5. Паверхня прызмы.
Прыклады не простых паверхняў:
1. Ластаўкін хвост (звязная, але мае тапалагічна асаблівы пункт).
2. Двухпаласцевы гіпербалоід (не мае тапалагічна асаблівых пунктаў, ала і не звязная).
