
- •2. Элементарная крывая. Агульныя крывыя. Простыя крывыя.
- •5. Гадкая (рэгулярная) элементарная крывая.
- •10. Датычная прамая крывой.
- •11. Нармаль плоскай крывой. Нармальная плос-касць прасторавай крывой. Вугал паміж крывымі.
- •12. Даўжыня дугі крывой. Формулы для вылічэння даўжыні дугі.
- •15. Суправаджальны трохграннік. Кананічны базіс.
- •17. Крывізна і кручэнне.
- •20. Крывізна і кручэнне акружнасці, гарфіка функцыі, шрубавай лініі.
- •21. Крывая нулявой крывізны. Пункты спрамлення (выпроствання).
- •22. Крывая нулявога кручэння. Пункты сплашчэння.
- •23. Натуральныя раўнанні. Асноўная тэарэма тэорыі крывых.
- •27. Элементарная паверхня (э.П.). Агульная павер-хня (а.П.). Простая паверхня (п.П.).
- •29. Гладкая (рэгулярная) элементарная паверхня.
- •35. Датычная плоскасць паверхні.
- •36. Нармаль паверхні. Кананічны базіс.
- •37. Першая квадратычная форма параметрызава-най паверхні. Запіс першай квадратычнай формы ва унутраных каардынатах. Дыскрымінант першай ква-дратычнай формы.
- •38. Вылічэне даўжыні дугі крывой на паверхні.
- •39. Вылічэнне вугла паміж крывымі на паверхні.
- •40. Вылічэнне плошчы абсягу на паверхні.
- •41. Другая квадратычная форма параметрызава-най паверхні.
29. Гладкая (рэгулярная) элементарная паверхня.
Э.п.
называецца
паверхняй класа
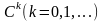 калі яна дапускае параметрызацыю
калі яна дапускае параметрызацыю
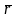 класа
класа
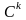 .
Пры
.
Пры
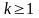 паверхню называюць k
разоў непарыўна дыферанца-вальнай.
Паверхні належачыя класу
паверхню называюць k
разоў непарыўна дыферанца-вальнай.
Паверхні належачыя класу
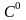 ,
але не належа-чыя класу
,
але не належа-чыя класу
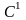 не разглядываюцца ў дыферынцыальнай
геаметрыі, паверхні класа
наз. Непарыўнымі.
не разглядываюцца ў дыферынцыальнай
геаметрыі, паверхні класа
наз. Непарыўнымі.
Заўвага: паверхні непарыўна дыферынцыяльныя, так-сама могуць мець дрэнныя пункты і г.д.
Прыклад.
Цыліндр
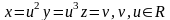 мае прамую дрэнных пунктаў
мае прамую дрэнных пунктаў
 у плоскасці Оху.
у плоскасці Оху.
Э.п.
называецца
гладкай (рэгулярнай) класа
,
,
калі яна дапускае параметрызацыю
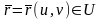 такую, што, па-першае,
такую, што, па-першае,
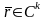 і па-другое,
і па-другое,
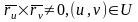 (1).
(1).
Заўвага:
умова (1) вызначае, што
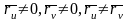 ,
,
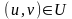
Заўвага: рэгулярная паверхня можа дапускаць і нерэ-улярную параметрызацыю.
35. Датычная плоскасць паверхні.
Азн.
Датычнай плоскасцю (да) паверхні
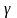 яе п.Р наз. плоскасць
яе п.Р наз. плоскасць
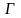 ,
якая праходзіць праз п.Р і змяшчае
датычныя прамыя да ўсіх крывых на
паверхні
,
што праходзіць праз гэты пункт.
,
якая праходзіць праз п.Р і змяшчае
датычныя прамыя да ўсіх крывых на
паверхні
,
што праходзіць праз гэты пункт.
Тэарэма:
усякая
рэгулярная (гладкая) э.п.
у кожным сваім п.Р мае датычную плоскасць
Т і пры тым толькі адну, калі
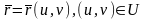 дапшчальная параметрыза-цыя паверхні
тады нармальным вектарам датычнай
плоскасці
у п.
дапшчальная параметрыза-цыя паверхні
тады нармальным вектарам датычнай
плоскасці
у п.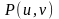 з’яўляецца вектар
з’яўляецца вектар
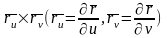 .
.
Доказ.
(1)
Існаванне. Няхай
адвольная гладкая крывая, якая праходзіць
праз п.
на параметрызаванай паверхні
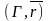 і ляжыць на
і няхай
і ляжыць на
і няхай
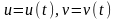 яе дапушчаль-ныя параметрычныя раўнанні.
яе дапушчаль-ныя параметрычныя раўнанні.
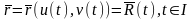 .
Знойдзем кіроўны вектар датычнай прамой
да
у п.Р:
.
Знойдзем кіроўны вектар датычнай прамой
да
у п.Р:
 .
Т.ч. кіроўны вектар усіх датычных пра-мых
да крывых на па-верхні
у п.Р раскладваюцца па азісу
.
Т.ч. кіроўны вектар усіх датычных пра-мых
да крывых на па-верхні
у п.Р раскладваюцца па азісу
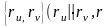 - гладкая параметрызацыя), г.зн. што усе
указанныя датычныя прамыя ляжаць у
адной плос-касці, якая змяшчае вектары
- гладкая параметрызацыя), г.зн. што усе
указанныя датычныя прамыя ляжаць у
адной плос-касці, якая змяшчае вектары
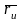 і
і
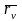 адкладзенныя ад п.Р.
адкладзенныя ад п.Р.
(2)
Адзінасць. Няхай
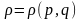 ,
,
 эквівалентная параметрызацыя паверхні
эквівалентная параметрызацыя паверхні
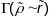 ,
тады
,
тады
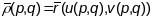 і дыферыцчуючы па
і дыферыцчуючы па
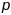 і
і
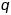 маем :
маем :
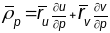 ,
,
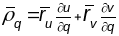 .
Тады:
.
Тады: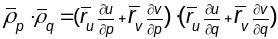 =
=

Паколькі
Якабіян не роўны 0 у кожным пункце мноства
V,
таму калі
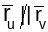 ,
то
,
то
 ,
г.зн. што вектары
,
г.зн. што вектары
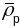 і
і
 утвараюць базіс той жа самай плоскасці
утвараюць базіс той жа самай плоскасці
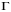 ,
што і трэба было даказаць.
,
што і трэба было даказаць.
(3)
Канструктыўная частка. Паколькі вектары
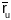 і
і
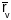 утвараюць базіс датычнай плоскасці
у п.
утвараюць базіс датычнай плоскасці
у п.
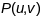 азначэнню вектарнага здабытку, вектар
азначэнню вектарнага здабытку, вектар
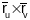 будзе нармальным вектарам плоскасці
.
Што і трэба было даказаць.
будзе нармальным вектарам плоскасці
.
Што і трэба было даказаць.
Заўвага:
вектары
і
вылічаныя у п.
параметрычнай паверхні
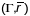 з’яўляюцца кіроўнымі вектарамі
каардынатных ліній,
з’яўляюцца кіроўнымі вектарамі
каардынатных ліній,
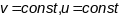 ,
якія праходзяць праз п.Р.
,
якія праходзяць праз п.Р.
Пры
вылічэнні
дапускаем:
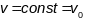 .
Атрымліваем:
.
Атрымліваем:
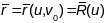 і таму
і таму
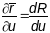 *****
-
гэта і есць кіроўны вектар датычнай
прамой
*****
-
гэта і есць кіроўны вектар датычнай
прамой
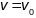 .
Аналагічна для
.
.
Аналагічна для
.
36. Нармаль паверхні. Кананічны базіс.
Нармалю паверхні Г у п.Р называецца прамая n, якая праходзіць праз п.Р і перпендыкулярна датычнай плоскасці Г к поверхні Г у гэтым пункце.
Сцверджанне: кожная гладкая паверхня ў кожным сваім пункце мае нармаль n і пры тым толькі адну.
Калі
 адвольная дапушчальная параметрыза-цыя
паверхні Г, тады вектар
адвольная дапушчальная параметрыза-цыя
паверхні Г, тады вектар
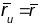 з’яўляецца кіроўным вектарам нармалі
n
паверхні
з’яўляецца кіроўным вектарам нармалі
n
паверхні
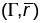 у п.
у п.
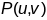 .
.
Кананічным
базісам гладкай параметрызаванай
паверхні
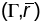 у яе п.
называецца правая тройка вектароў
у яе п.
называецца правая тройка вектароў
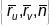 ,
дзе
,
дзе
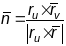 - орт нармалі.
- орт нармалі.
Заўвага: калі паверхня зададзена яўна ці неяўна ў дэкартавых каардынатах не абавязкова пераходзіць да яе параметрычных раўнанняў.
Сцверджанне:
калі
гладкая паверхня Г задавальняе раўнанню
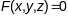 без асабліввых пунктаў (г.зн.
без асабліввых пунктаў (г.зн.
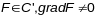 *),
тады вектар
*),
тады вектар
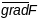 есць нармальны вектар датычнай плоскасці
Г, ці што тое самае, кіроўны вектар
нармалі n
паверхні Г у яе п.
.
есць нармальны вектар датычнай плоскасці
Г, ці што тое самае, кіроўны вектар
нармалі n
паверхні Г у яе п.
.
Доказ.
Няхай
- адвольная гладкая крывая на паверхні
Г, якая праходзіць праз п.
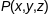 і
і
 - першыя дапушчальные параметрычныя
раўнанні ва унутранных каардынатах.
Калі
- першыя дапушчальные параметрычныя
раўнанні ва унутранных каардынатах.
Калі
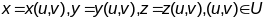 гладкія
параметрычныя раўнанні Г, тады адпаведныя
параметрычныя раўнанні крывой
у дэкартавых каардынатах будуць мець
выгляд:
гладкія
параметрычныя раўнанні Г, тады адпаведныя
параметрычныя раўнанні крывой
у дэкартавых каардынатах будуць мець
выгляд:
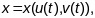
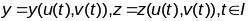 .
Уздоўж крывой
будзем мець:
.
Уздоўж крывой
будзем мець:
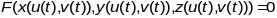
Дыферынцуючы па t будзем мець:
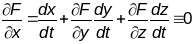 уздоўж
, ці, што тое самае
уздоўж
, ці, што тое самае
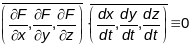
Г.зн.
у п.
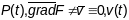 -
кіроўны вектар датычнай прамой да крывой
у п.Р. Т.ч.
-
кіроўны вектар датычнай прамой да крывой
у п.Р. Т.ч.
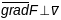 для
для
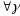 што і трэба было даказаць.
што і трэба было даказаць.
