63. Решение систем линейных уравнений методами Гаусса и Крамера.

Теорема Крамера. Пусть - определитель матрицы системы , а - определитель матрицы, получаемой из матрицы заменой столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам: ( ).

Пример. Решить систему уравнений .

Вычислим определители: , , , .

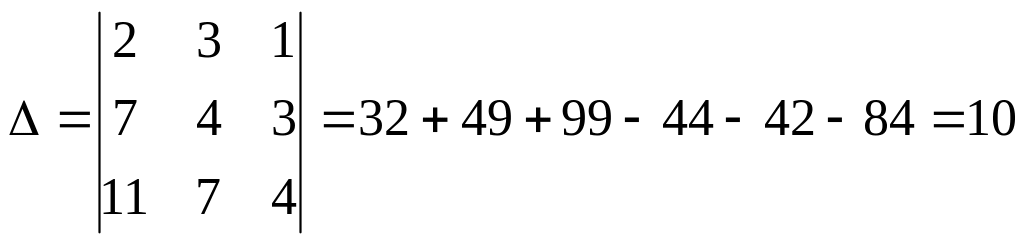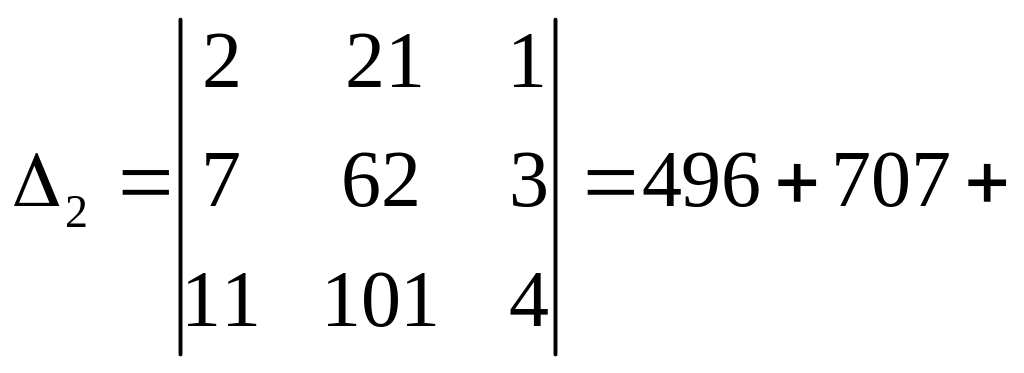
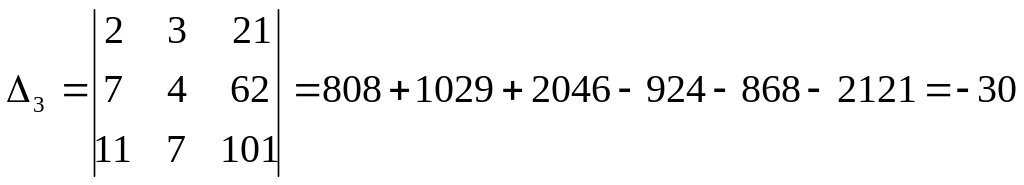Итак, , , .

Рассмотрим систему линейных алгебраических уравнений .

Решим систему методом Гаусса. Предположим, что (иначе найдем такое, что и переставим уравнением с местами).

Умножим уравнение на и прибавим ко второму уравнению. Умножим уравнение на и прибавим к уравнению.

Таким образом, в результате этих преобразований мы получим систему, эквивалентную данной: .

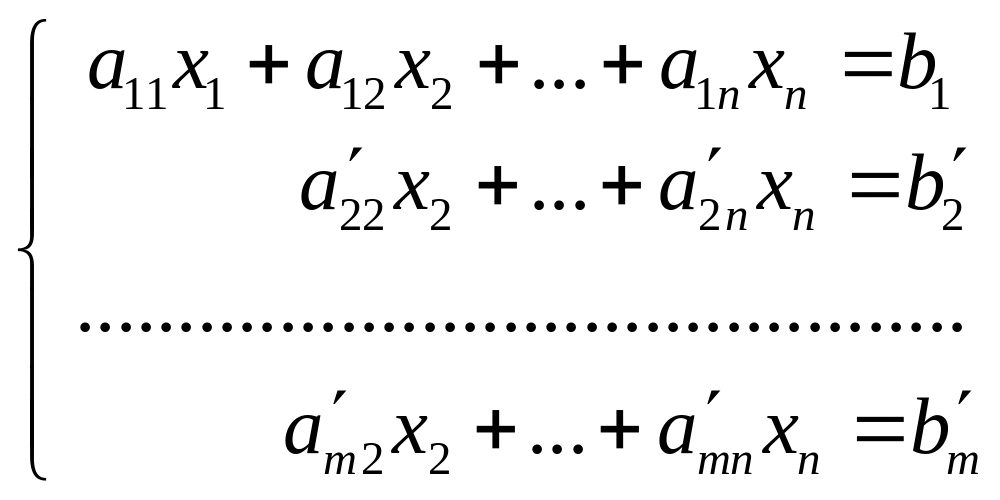Если в процессе исключения мы получим противоречие , то система в этом случае несовместна, а значит несовместна и система .

Предположим, что такого равенства мы не получили. Тогда из 3, 4, …, уравнений исключаем аналогичным образом: умножим уравнение на и прибавляем к , в результате исключается из уравнения.

Если в полученной системе нет противоречивых равенств, то исключаем из 4, 5, …, уравнений …, продолжая этот процесс, получим, что:

1) система приводится к треугольному виду;

2) система приводится к виду трапеции;

3) в процессе исключения переменных появляется противоречивое равенство.

В случае 1) система имеет единственное решение, в случае 2) – бесконечно много решений, в случае 3) система несовместна.

Пример. Решить систему уравнений .

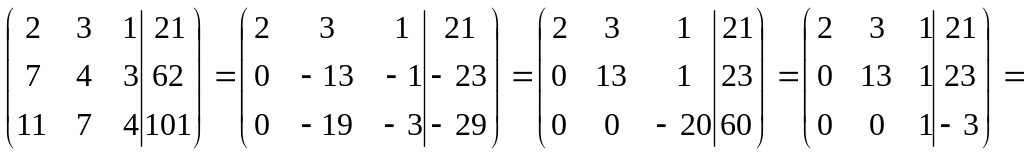
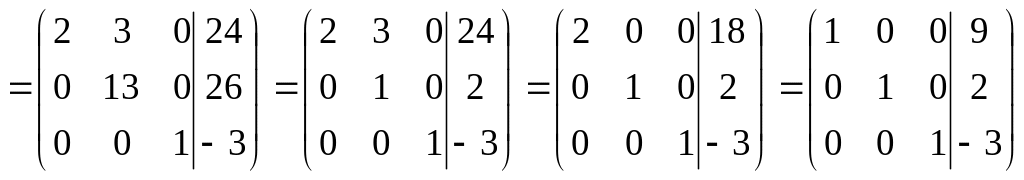. Так как ранг матрицы совместной системы равен числу переменных, то система имеет единственное решение, следовательно, , , .