
- •30. Экстремумы функции нескольких переменных. Понятие о векторе градиента функции двух переменных.
- •31. Понятие первообразной, основные свойства.
- •24. Интегрирование способом подстановки.
- •25. Метод интегрирования по частям.
- •27. Разложение действительного многочлена на множители.
- •28. Разложение рациональной функции на простейшие дроби.
- •29.Интегрирование рациональных функций.
- •30. Интегрирование простейших иррациональностей.
- •31. Биномиальный интеграл.
- •32. Интегрирование функции .
- •33 . Интегрирование функции , (первая подстановка Эйлера).
- •34 . Интегрирование функции , (вторая подстановка Эйлера).
- •35 . Интегрирование функции , (третья подст.Эйлера).
- •36. Определенный интеграл и его геометрический смысл.
- •37. Основные свойства определенного интеграла.
- •38. Основные условия интегрируемости функций.
- •39. Связь определенного интеграла с первообразной. Формула Ньютона-Лейбница
- •50. Интегрирование функций, заданных на бесконечном интервале.
- •43. Вычисление площади плоской фигуры.
- •44. Вычисление объема тела вращения.
- •45. Вычисление длины дугиплоской кривой.
- •46. Вычисление площади поверхности тела вращения.
- •57. Векторное пространство. Линейная зависимость векторов.
- •58. Базис векторного пространства. Матрицы, действия с матрицами.
- •59. Определители. Свойства определителей
- •61. Ранг матрицы, обратная матрица.
- •62. Системы линейных уравнений, решения систем, свойства. Однородные и неоднородные системы.
- •63. Решение систем линейных уравнений методами Гаусса и Крамера.
24. Интегрирование способом подстановки.
Метод
замены переменной описывается формулой:
![]() ,
где
,
где
![]() - функция, дифференцируемая на
рассматриваемом промежутке.
- функция, дифференцируемая на
рассматриваемом промежутке.
Пример.
Вычислить неопределенный интеграл
![]() .
.
![]() .
Пусть
.
Пусть
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
![]()
25. Метод интегрирования по частям.
Интегрирование
по частям. Пусть
![]() и
и
![]() - дифференцируемые функции, тогда
- дифференцируемые функции, тогда
![]() .Пример.
Вычислить
.Пример.
Вычислить
![]() .
.
Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
![]()
![]() .
.
27. Разложение действительного многочлена на множители.
Теорема.
Если
![]() и
и
![]() - корни квадратного уравнения, то
справедливо следующее разложение
- корни квадратного уравнения, то
справедливо следующее разложение
![]() .
.
Пример.
Разложить квадратный трехчлен
![]() на множители. По теореме Виета определим
корни квадратного трехчлена:
на множители. По теореме Виета определим
корни квадратного трехчлена:
![]() ,
откуда
,
откуда![]() ,
,
![]() .
Итак,
.
Итак,
![]() .
.
Разложить многочлен на множители означает представить его в виде произведения многочленов. Для этого используют различные приемы. Рассмотрим некоторые из них.
1.Вынесение общего множителя за скобку:
![]() .
.
2. Группировка слагаемых:
![]() .
.
3. Формулы
сокращенного умножения:
![]() ,
,
![]() ,
,
![]() ;
;![]() ,
,
![]() ;
;![]() ,
,
![]() .
.
Теорема.
Пусть дан многочлен
![]() степени,
степени,
![]() ,
,
![]() .
Разложение
.
Разложение
![]() является для многочлена
единственным с точностью до порядка
сомножителей.
является для многочлена
единственным с точностью до порядка
сомножителей.
28. Разложение рациональной функции на простейшие дроби.
Когда степень многочлена знаменателя дроби равна нулю (т.е. в знаменателе стоит число), дробь является многочленом. По теореме известно, что любой многочлен может быть разложен на множители.
Если степень знаменателя дроби больше нуля и степень числителя меньше степени знаменателя, то дробь можно представить в виде простейших дробей. Если степень числителя больше дроби знаменателя, то необходимо выполнить деление многочлена на многочлен «углом».
Пример.
Разложить рациональную функцию
![]() на простейшие дроби.
на простейшие дроби.
![]()
![]()
![]() .
.
Определим
![]() ,
,
![]() ,
и
,
и
![]() из системы уравнений
из системы уравнений
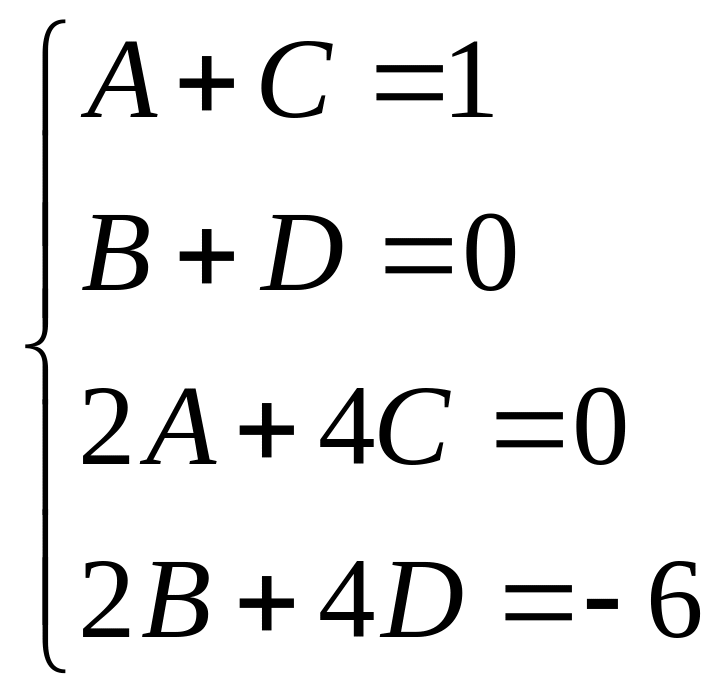 ,
,
![]() .
Итак,
.
Итак,
![]() .
.
29.Интегрирование рациональных функций.
Интегрирование рациональных функций сводится к разложению дроби на простейший и проинтегрировав каждое слагаемое.
Пример.
![]() .
.
![]()
![]() .
.
Определим
,
,
и
из системы уравнений
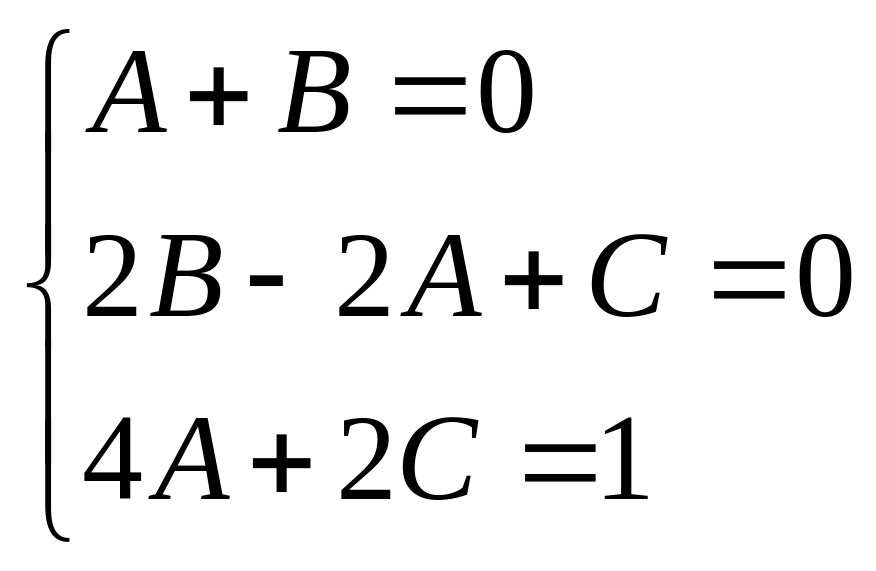 ,
,
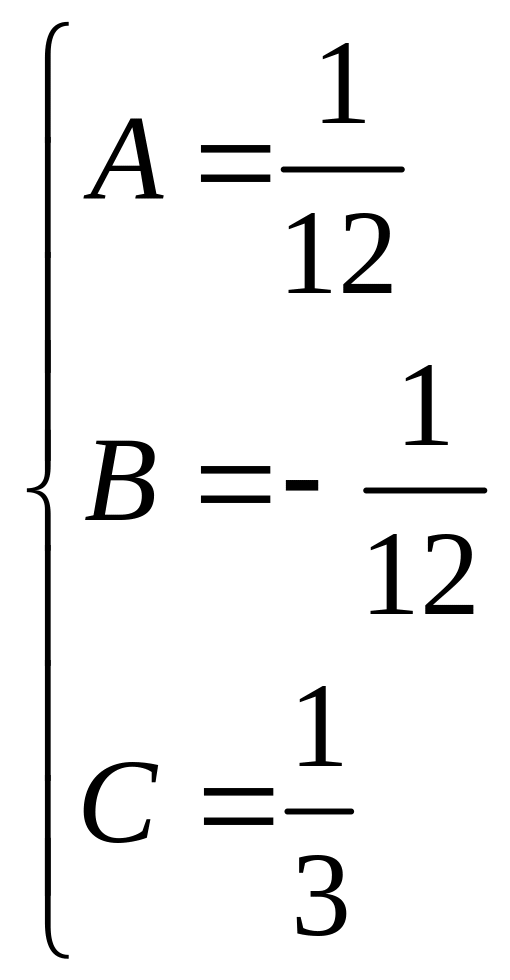 .
Итак,
.
Итак,
![]() .
.
![]()
![]()
![]()
![]() .
.
30. Интегрирование простейших иррациональностей.
Рассмотрим случаи, в которых замена переменной позволяет интегралы от иррациональных функций свести к интегралам от рациональных функций.
Обозначим
через
![]() функцию от переменных
функцию от переменных
![]() и
и
![]() ,
и некоторых постоянных, которая построена
с использованием лишь четырех
арифметических действий (сложения,
вычитания, умножения и деления). Например,
,
и некоторых постоянных, которая построена
с использованием лишь четырех
арифметических действий (сложения,
вычитания, умножения и деления). Например,
![]() ,
,
![]() и т.д.
и т.д.
Рассмотрим
интеграл вида
![]() .
Такие интегралы рационализируются
заменой переменной
.
Такие интегралы рационализируются
заменой переменной
![]() .
.
Пример.
Вычислить
![]() .
.
Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
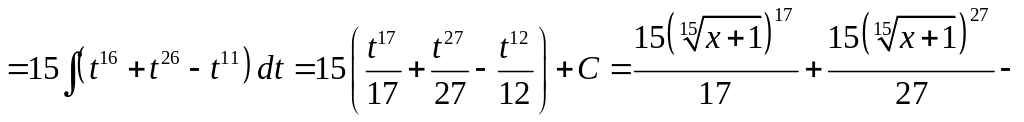
 .
.
31. Биномиальный интеграл.
Биномиальным
дифференциалом наз-ся выражение
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() - рациональные числа.
- рациональные числа.
Интеграл
от биномиального дифференциала
![]() приводится к интегралу от рациональной
функции в следующих трех случаях.
приводится к интегралу от рациональной
функции в следующих трех случаях.
Случай
1. Показатель степени
- целое число. Тогда интеграл
сводится к интегралу от рациональной
функции с помощью подстановки
![]() ,
где
,
где
![]() - общий знаменатель дробей
и
.
- общий знаменатель дробей
и
.
Случай
2. Число
![]() - целое. Тогда сводится к интегралу от
рац.функции с помощью подстан.
- целое. Тогда сводится к интегралу от
рац.функции с помощью подстан.
![]() ,
,
![]() - знаменатель дроби
.
- знаменатель дроби
.
Случай
3. Число
![]() - целое. Тогда интеграл
рационализируется с помощью подстановки
- целое. Тогда интеграл
рационализируется с помощью подстановки
![]() ,
где
- знаменатель дроби
.
,
где
- знаменатель дроби
.
Пример.
Найти интеграл
![]() .
.
Здесь
![]() ,
,
![]() ,
,
![]() - целое число, т.е. имеет место первый
случай интегрируемости. Поэтому следует
применить подстановку
- целое число, т.е. имеет место первый
случай интегрируемости. Поэтому следует
применить подстановку
![]() ,
тогда
,
тогда
![]() ,
,
![]() и данный интеграл принимает вид
и данный интеграл принимает вид
![]()
![]()
