39. Связь определенного интеграла с первообразной. Формула Ньютона-Лейбница

Теорема. Если функция непрерывна на отрезке , то найдется такое значение , что .

Доказательство. По свойству функции, непрерывной на отрезке, для произвольного значения из верно, что , где и - наименьшее и наибольшее значения функции на . Тогда, имеем .

Но функция, непрерывная на отрезке, принимает любое значение, заключенное между наименьшим и наибольшим значениями. Поэтому, в частности, найдется такое число , что или .

Теорема. Пусть функция непрерывна на отрезке и - любая первообразная для на . Тогда определенный интеграл от функции на равен приращению первообразной на этом отрезке, т.е. .

Доказательство. Пусть - некоторая первообразная для функции . По теореме (если функция непрерывна на отрезке , тогда в каждой точке отрезка производная функции по переменному верхнему пределу равна подынтегральной функции ), т.е. 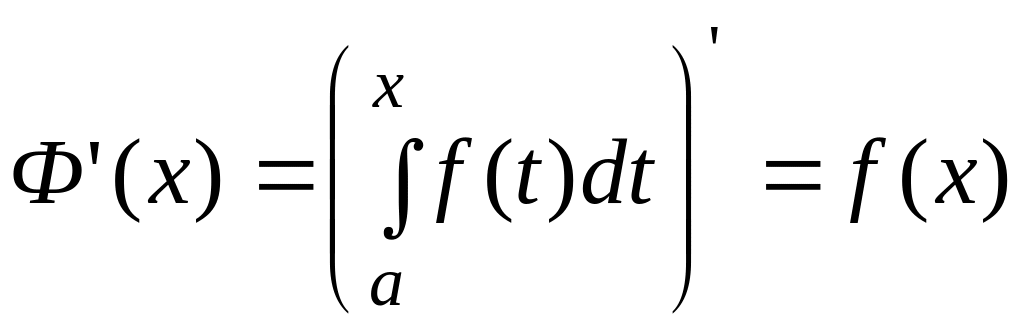функция , заданная формулой , также является первообразной для функции .

По теореме: если и - первообразные для функции на промежутке , то найдется такое число , что будет справедливо равенство ) найдется такое число , что .

Тогда для приращения первообразной имеем . Так как , то .

Пример. Вычислить .

.

41.Замена переменной в определенном интеграле

Теорема. Пусть функция имеет непрерывную производную на отрезке , , и функция непрерывна в каждой точке вида , где . Тогда справедливо следующее равенство .

Пример. Вычислить определенный интеграл .

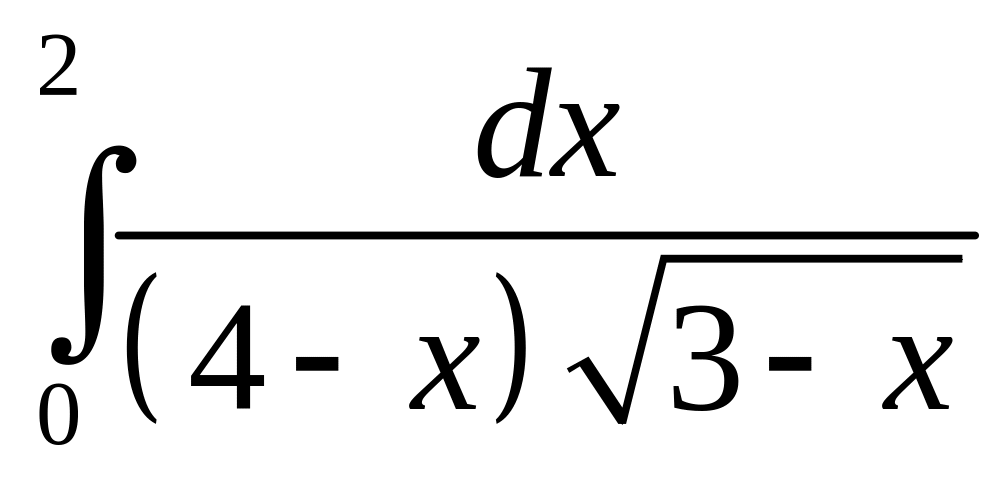Пусть , , , , , тогда .

42.Вычисление определенного интеграла по частям.

Теорема. Пусть функции и имеют непрерывные производные на отрезке . Тогда .

Пример. Вычислить .

Пусть , , , , тогда .Вычислим . .

Итак, .

48. Интегрирование функций, неопределенных в конечном числе точек.

Определение. Несобственным интегралом от функции на полуинтервале называется предел , где , т.е. .

Пример. Вычислить несобственный интеграл или доказать его расходимость.

.

Вычислим . Пусть , , , , тогда

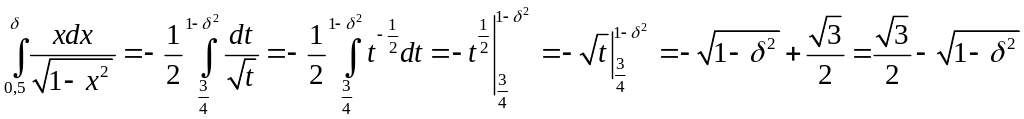
Итак, .

49. Интегрирование функций, имеющих разрывы второго рода

Для установления сходимости или расходимости несобственных интегралов с бесконечным верхним пределом интегрирования часто используется следующий признак.

Пусть при справедливо неравенство , где и - непрерывные знакоположительные функции. Тогда:

1. если сходимости 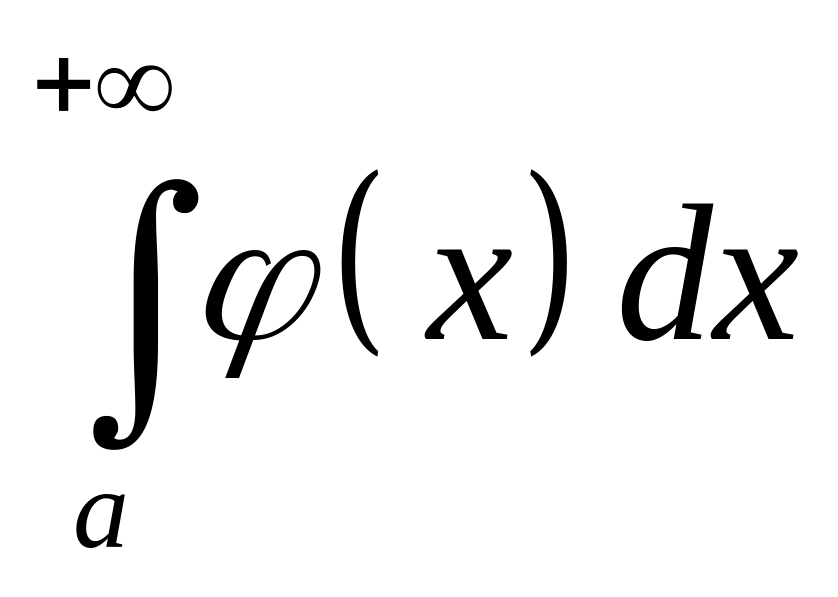, то сходится ;

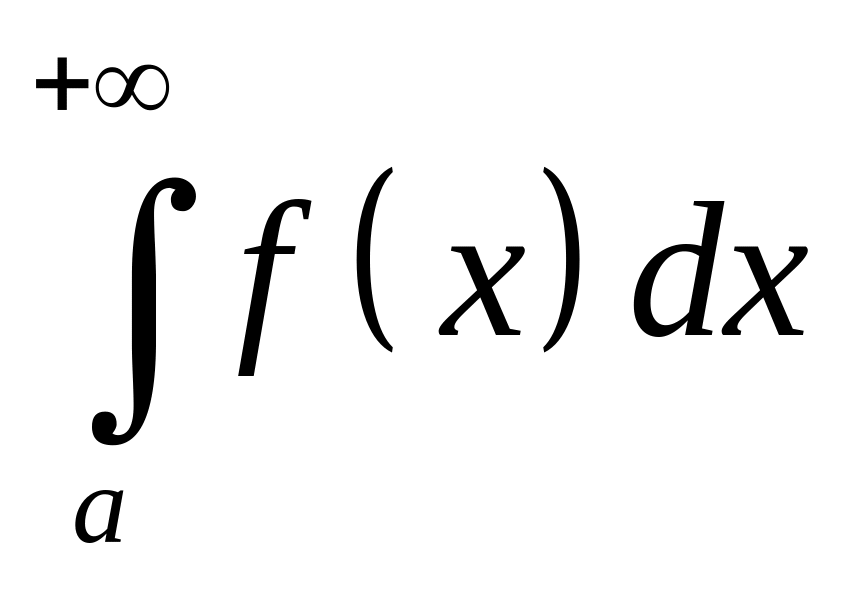2. если расходится , то расходиться и .

Аналогичный признак сравнения имеет место и для несобственных интегралов от разрывных функций.

Пример. Вычислить несобственный интеграл или доказать его расходимость: .

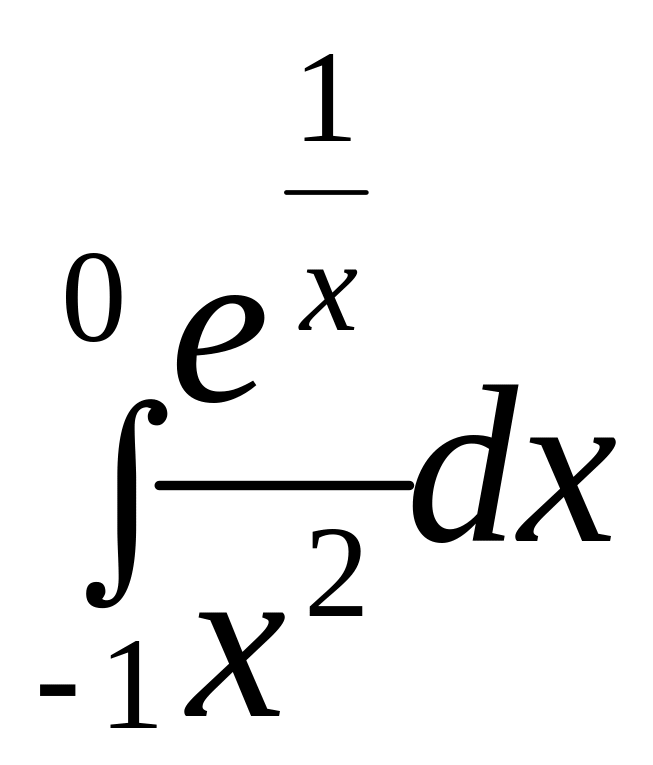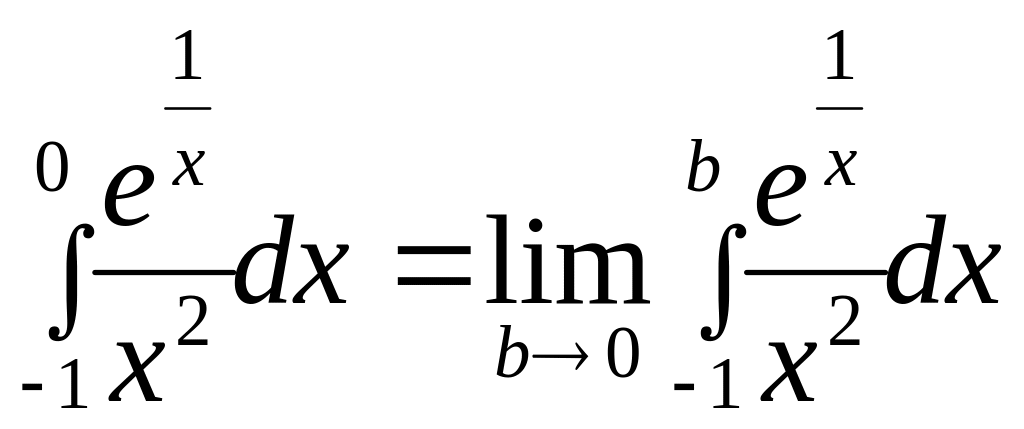. Пусть , , , , тогда . Несобственный интеграл расходится.

50. Интегрирование функций, заданных на бесконечном интервале.

Определение. Несобственным интегралом от функции на полуинтервале называется предел функции при , стремящемся к , т.е. .

Пример. Вычислить несобственный интеграл или доказать его расходимость.

.

Вычислим 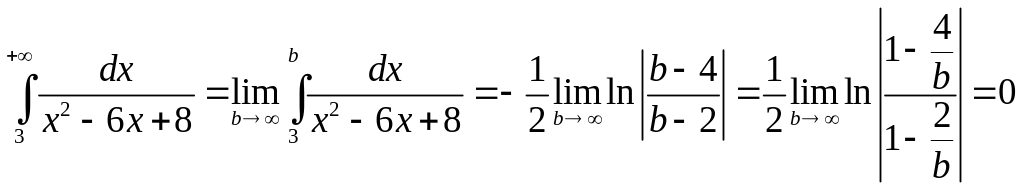. , , , , , , Т. к.интеграл , то он сходится.