58. Базис векторного пространства. Матрицы, действия с матрицами.
Определение. Совокупность линейно независимых векторов -мерного пространства называется базисом.
Теорема. Каждый вектор линейного пространства можно представить и притом единственным способом в виде линейной комбинации векторов базиса.
Теорема.
Если
- система линейно независимых векторов
пространства
и любой вектор а
линейно выражается через
,
то пространство
является
,
а векторы
- его базисом.
Пример.
Даны векторы
,
,
и
в некотором декартовом базисе. Показать,
что векторы
,
,
образуют базис и найти координаты
вектора
в этом базисе.
Покажем,
что векторы
,
,
образуют, т.е. составим векторное
равенство
и определим коэффициенты
,
и
.
.
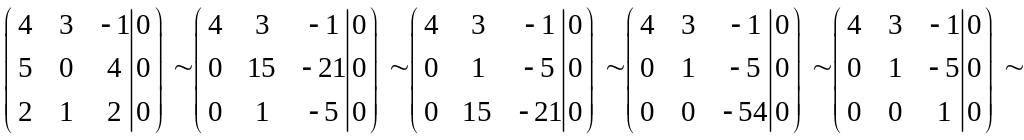
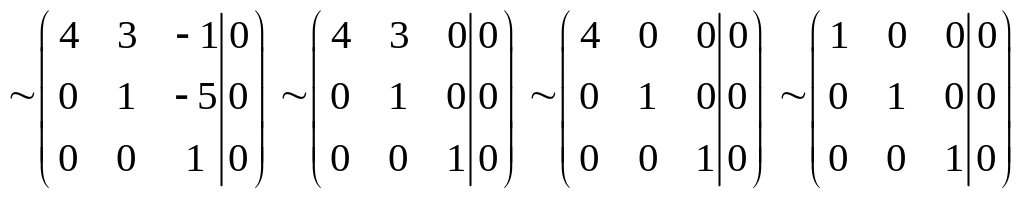Т. К..
,
то вектора
,
,
образуют базис.
Определим координаты вектора в этом базисе:
,
.
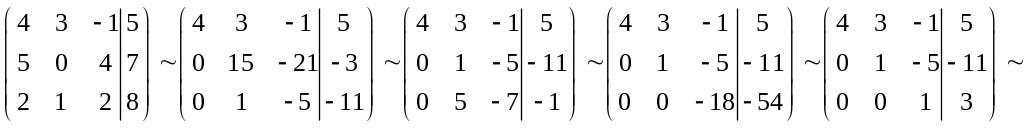
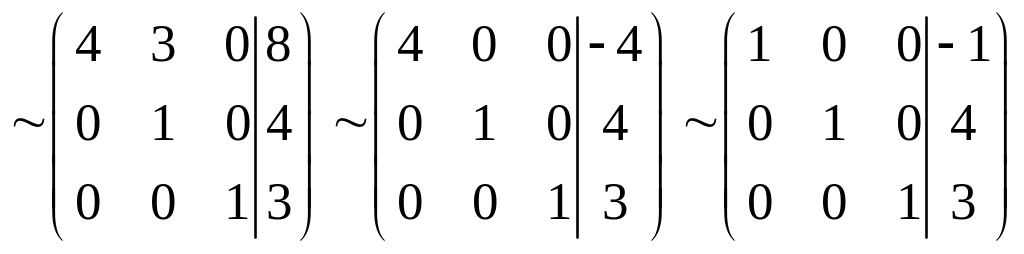Определение.
Матрицей размера
называется прямоугольная таблица чисел,
содержащая
строк и
столбцов. Числа, составляющие матрицу,
называются элементами матрицы.
Виды матриц:
- Матрица, состоящая из одной строки, называется матрицей (вектором) - строкой, а из одного столбца – матрицей (вектором) - столбцом.
- Матрица
называется квадратной
порядка, если число ее строк равно числу
столбцов и равно
.
- Матрица называется диагональной, если все недиагональные элементы квадратной матрицы равны нулю.
- Матрица называется единичной, если у диагональной матрицы порядка все диагональные элементы равны единице.
- Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю.
Операции над матрицами:
1.Умножение
м на число. Произведение матрицы
на число
называется матрица
,
элементы которой
для
;
.
2.Сложение
матриц. Суммой двух матриц
и
одинак. размера
называется матрица
,
элементы которой
для
;
.
3.Вычитание
матриц. Разность двух м. одинак.размера
определяется через предыдущ операции:
.
4. Умножение
матриц. Умножение матрицы
на матрицу
определено, когда число столбцов первой
матрицы равно числу строк второй.
Произведением матриц
называется матрица
,
каждый элемент которой
равен сумме произведений элементов
строки матрицы
на соответствующие элементы
столбца матрицы
.
5. Возведение
в степень. Целой положительной степенью
квадратной матрицы
называется произведение
матриц, равных
.
6. Транспонирование
матрицы. Транспонирование матрицы –
переход матрицы
к матрице
,
в которой строки и столбцы поменялись
местами с сохранением порядка.
Пример.
Выполнить
действия
.
.
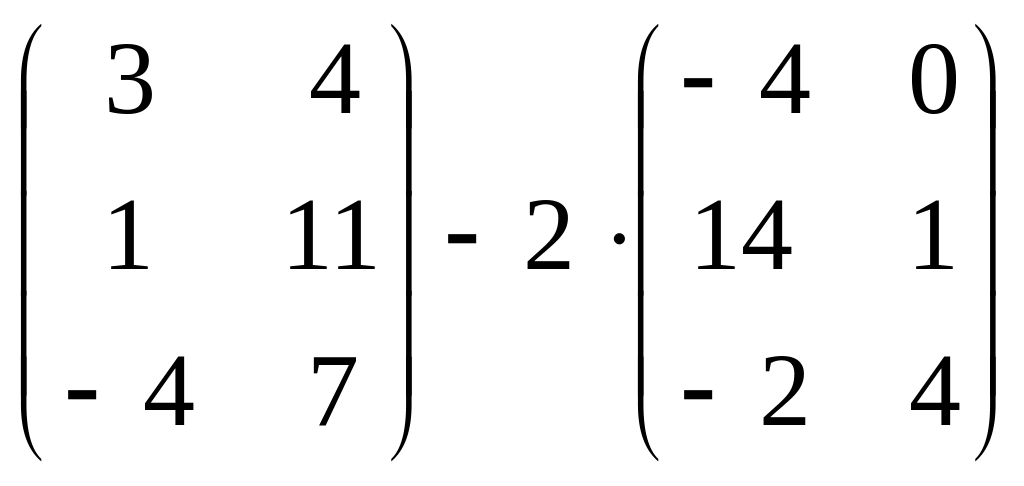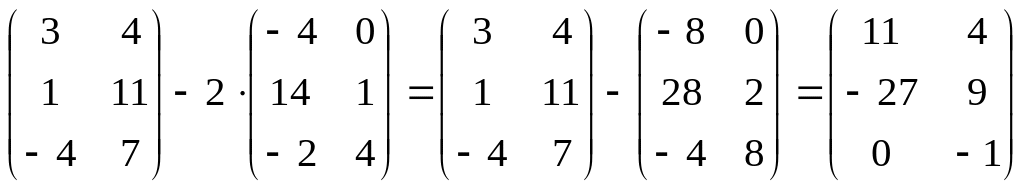59. Определители. Свойства определителей
Определитель
квадратной матрицы второго порядка
вычисляется по формуле:
.
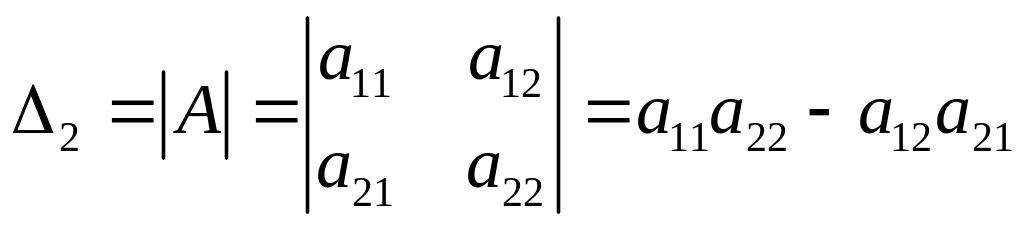Определителем
квадратной матрицы третьего порядка
может быть вычислен по правилу
треугольников, или правилу Сарруса:
.
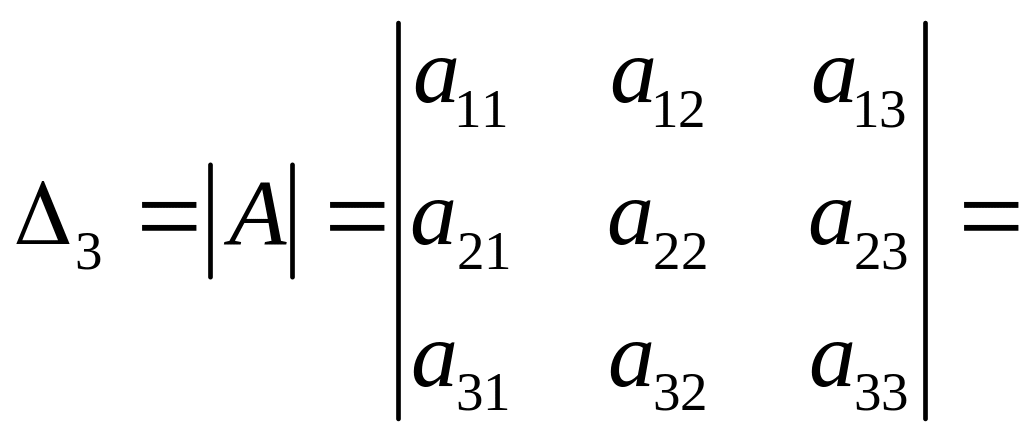
Определителем
квадратной матрицы
порядка, или определителем
порядка, называется число, равное
алгебраической сумме
членов, каждый из которых является
произведением
элементов матрицы, взятых по одному из
каждой строки и каждого столбца, причем
знак каждого члена определяется как
,
где
– число инверсий в перестановке
из номеров столбцов элементов матрицы,
если при этом номера строк записаны в
порядке возрастания:
,
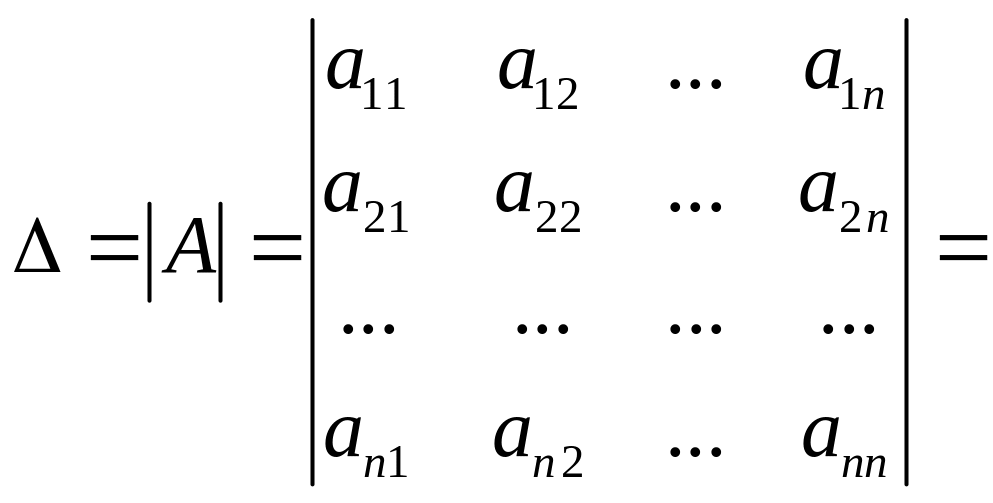
где сумма берется по всем перестановкам
.
Свойства определителей:
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то ее определитель умножиться на это число .
Пусть
определитель исходной матрицы равен
.
Для определенности первую строку матрицы
умножим на
,
получим новый определитель
,
который разложим по элементам первой
строки:
.
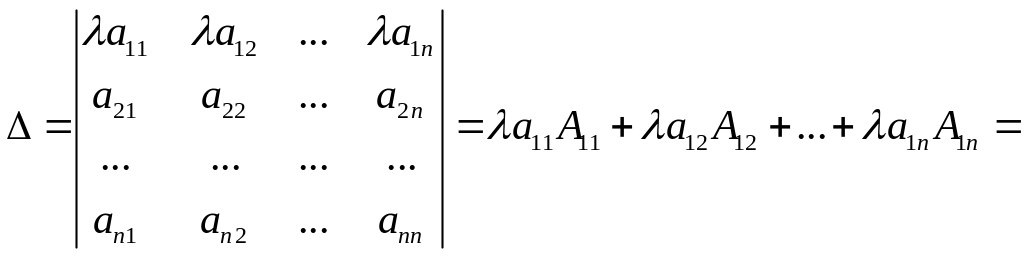
Замечание. За знак определителя можно выносить общий множитель любой строки или столбца.
3. При транспонировании матрицы ее определитель не изменяется.
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
Предположим
вначале, что переставлены две соседние
строки матрицы:
и
.
Разложим определитель исходной матрицы
по элементам
строки, а определитель новой матрицы
(с переставленными строками)
- по элементам
строки. Полученные разложения будут
отличаться только знаком, поэтому
.
Если
переставить не соседние строки, а скажем,
и
,
то такую перестановку можно представить
как последовательное смещение
строки на
строк вниз (при этом каждый раз знак
определителя меняется), а
строки на
вверх, что тоже сопровождается
изменением знака, т.е. знак поменяется
нечетное число
раз, т.е.
.
5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Действительно,
переставим эти строки (столбцы). С одной
стороны, определитель не изменится, но
с другой стороны, по свойству 4 поменяет
знак, т.е.
,
откуда
.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равен 0.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9. Сумма
произведений произвольных чисел
,
,
…,
на алгебраические дополнения элементов
любой строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на числа
,
,
…,
.
10. Определитель
произведения двух квадратных матриц
равен произведению их определителей:
,
где
;
и
- матрицы
порядка.
Пример.
Вычислить определитель
.
.
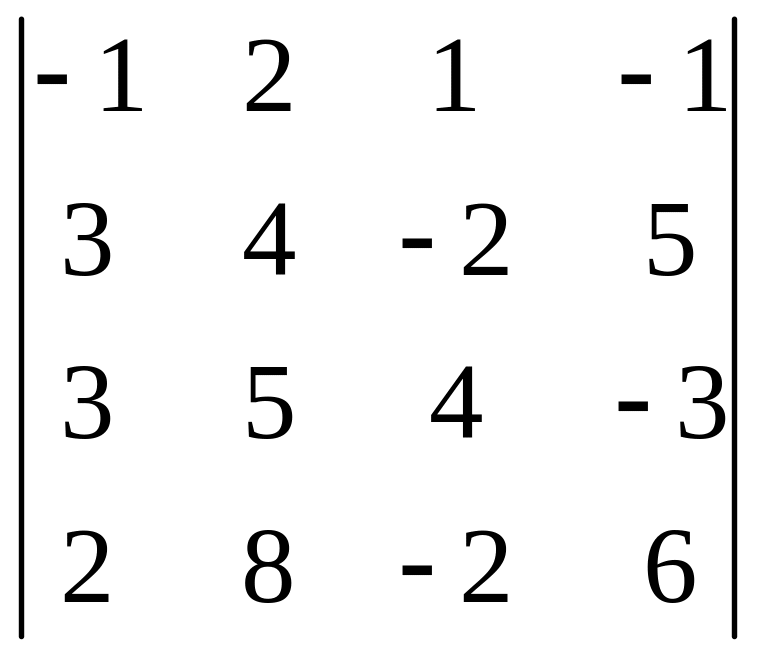
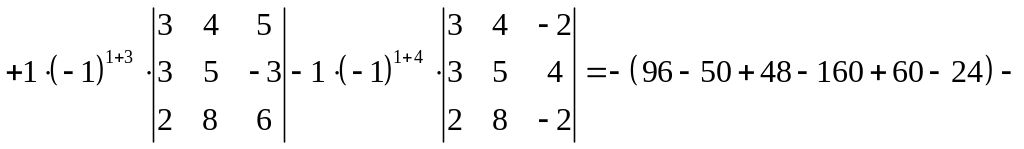