61. Ранг матрицы, обратная матрица.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы,

Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

Теорема. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).

Определение. Матрица называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: .

Теорема (необходимое и достаточное условие обратной матрицы). Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Алгоритм вычисления обратной матрицы:

1. Найти определитель исходной матрицы. Если 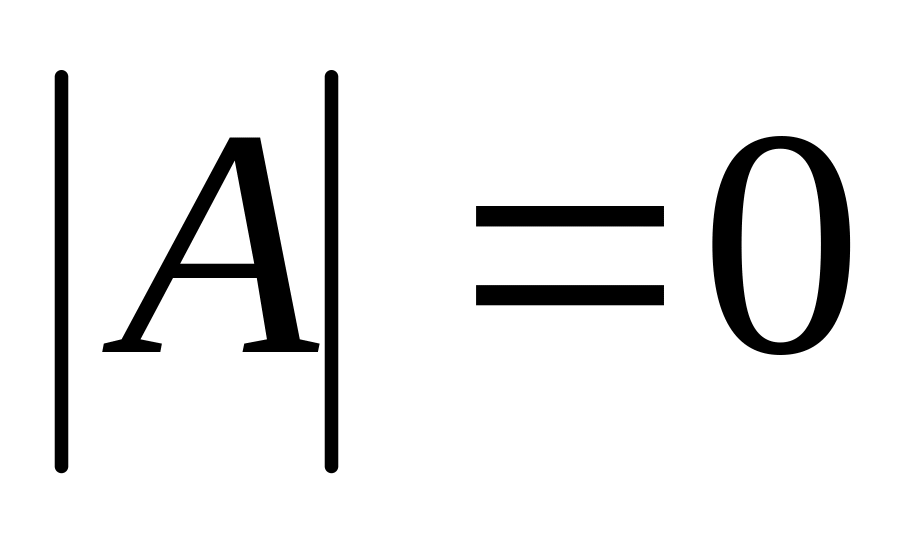, то матрица – вырожденная и обратной матрицы не существует.

2. Найти матрицу, транспонированную к данной.

3. Найти алгебраические дополнения элементов транспонированной матрицы.

4. Вычислить обратную матрицу по формуле: .

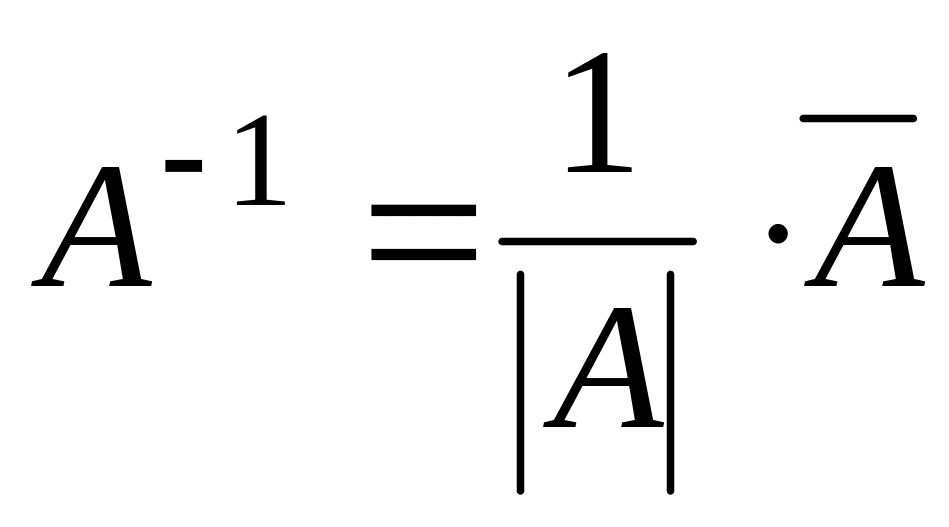5. Проверить правильность вычисления обратной матрицы, исходя из определении: .

Пример. Найти обратную матрицу .

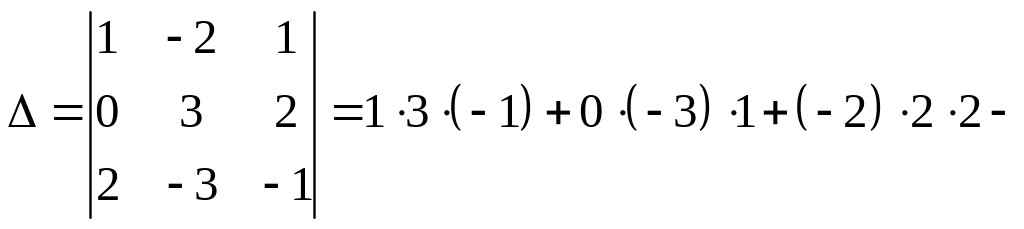
Определитель матрицы равен . Так как определитель матрицы не равен нулю, то существует обратная матрица .

Найдем алгебраические дополнения: , , ,

, ,

, ,

, .

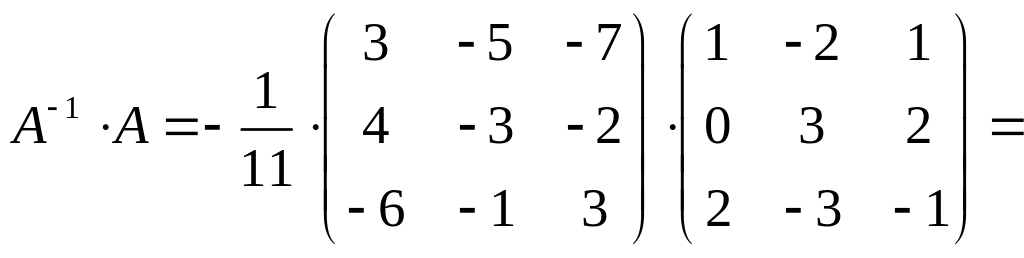
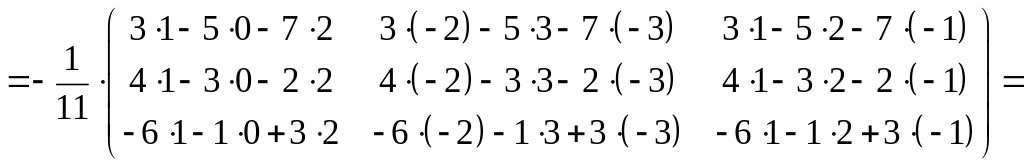
Обратная матрица имеет вид: . Проверим, правильно ли найдена обратная матрица: . Итак, обратная матрица найдена верно.

Пример. Решить матричное уравнение и сделать проверку: . .

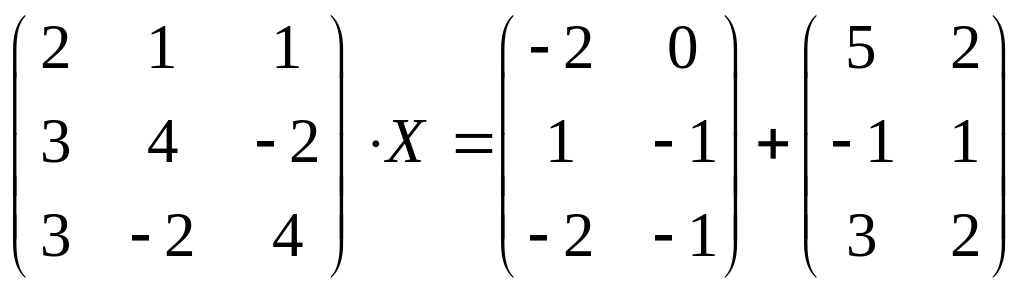
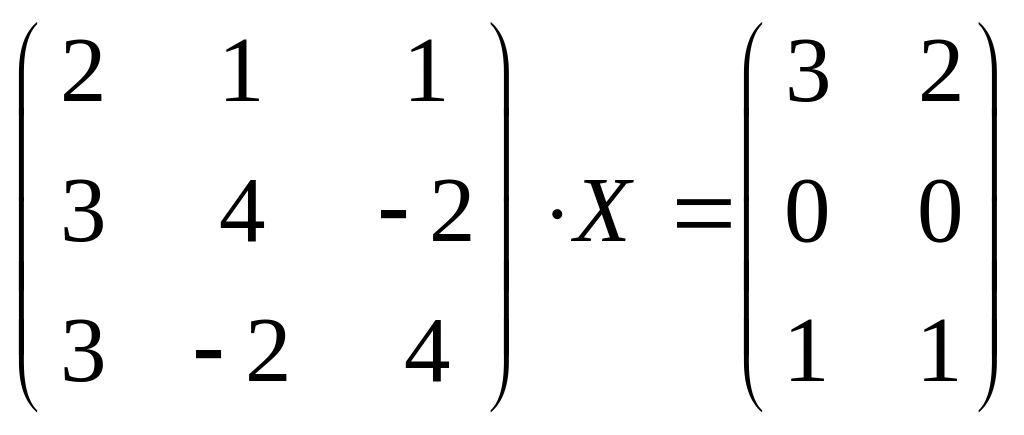Пусть , тогда .

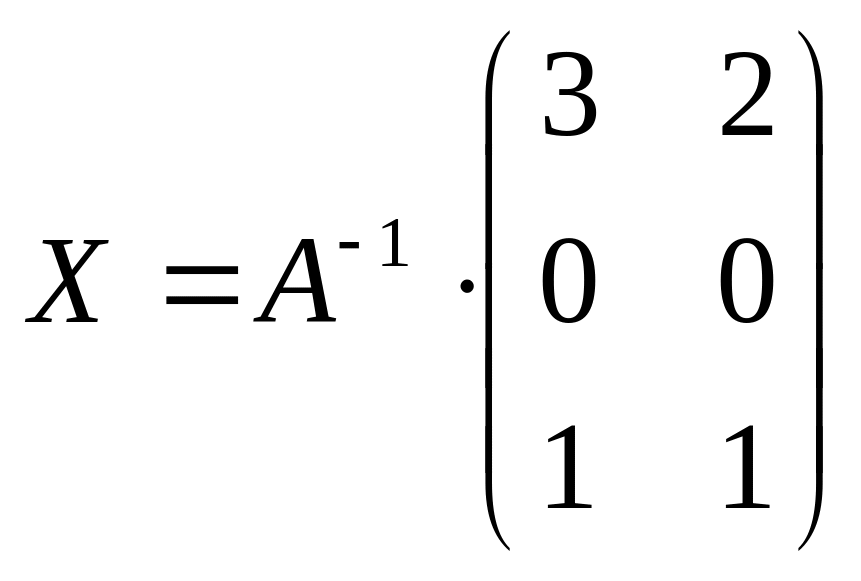Найдем . 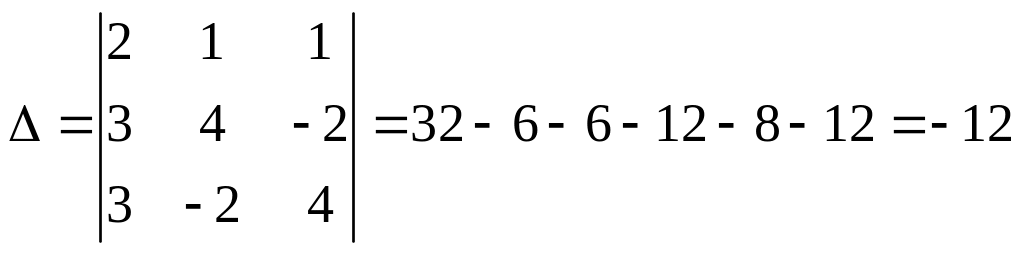, так как , то существует. Транспонированная матрица имеет вид: 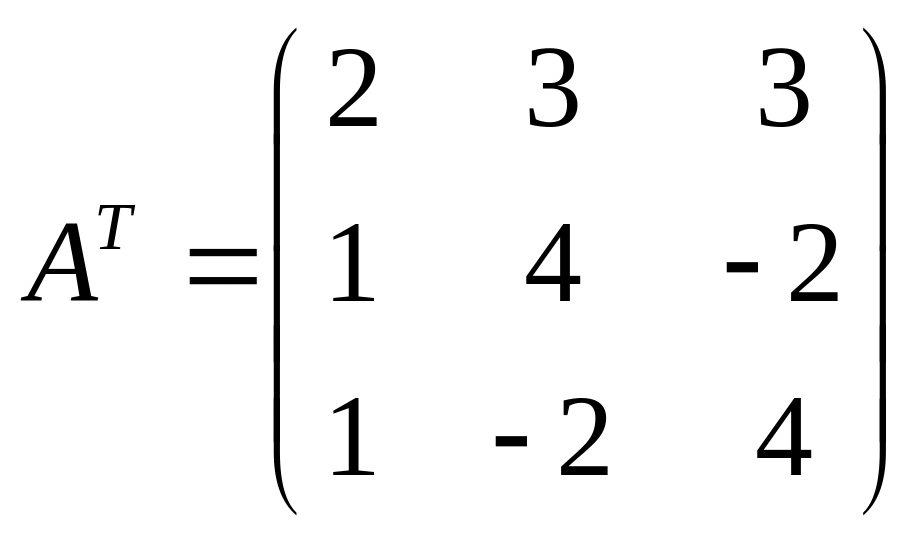. Найдем алгебраические дополнения для транспонированной матрицы: , , , , , , , , . Обратная матрица имеет вид: .Итак

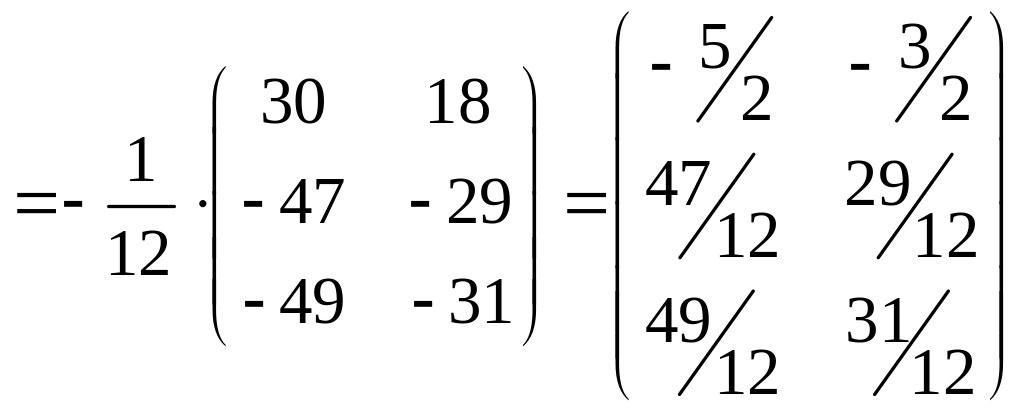
Проверка: , , , , , .

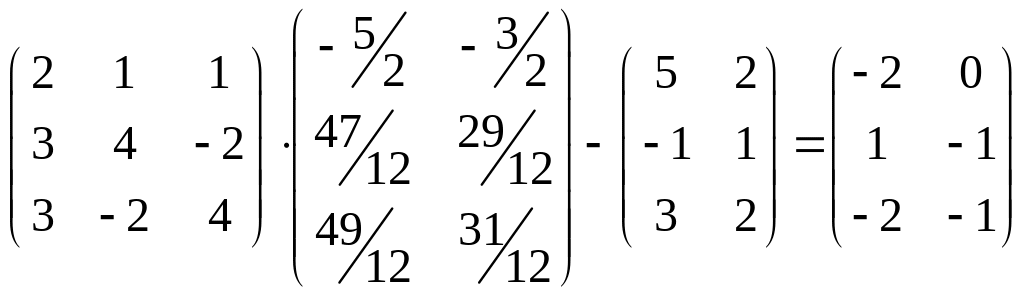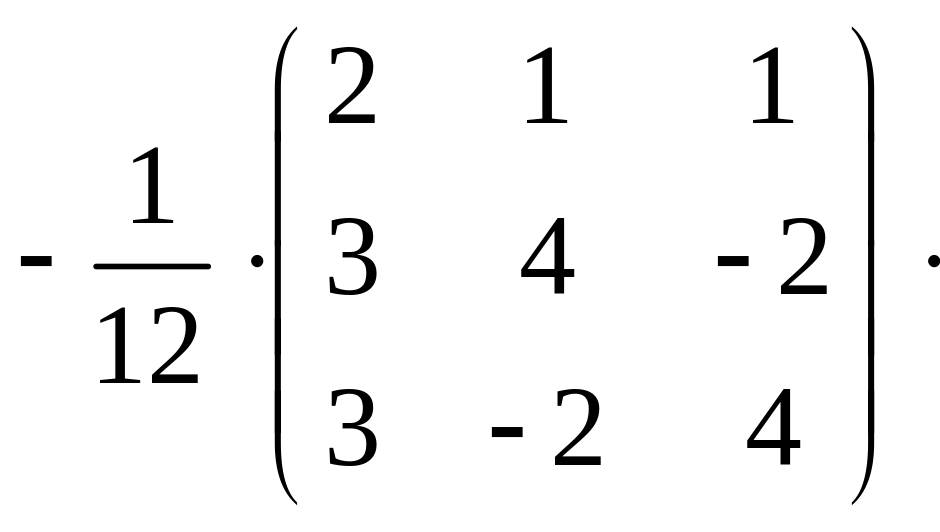
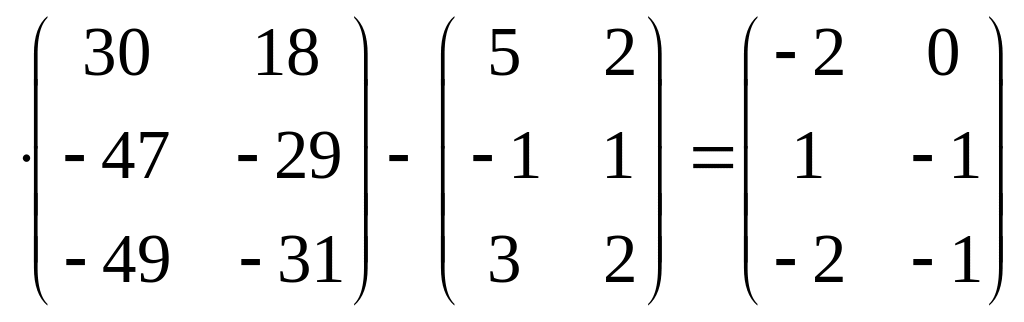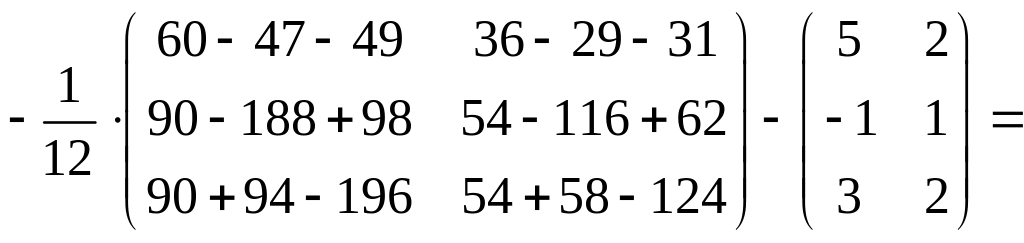
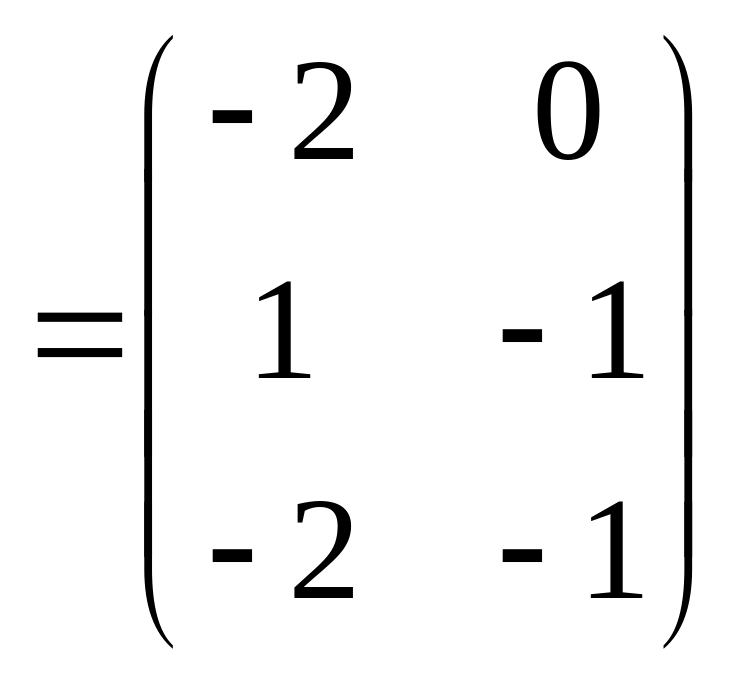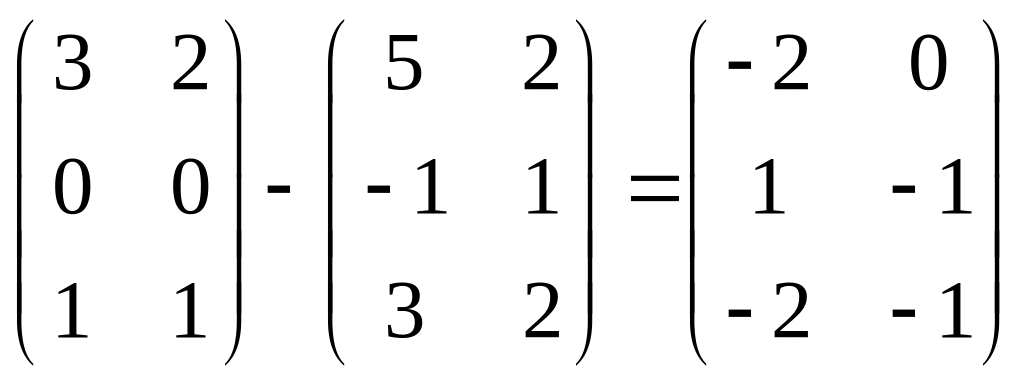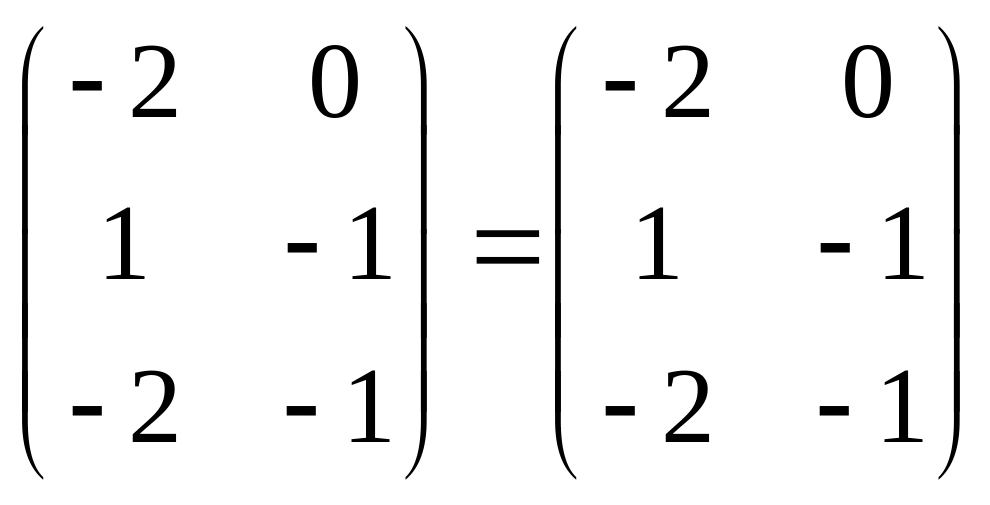62. Системы линейных уравнений, решения систем, свойства. Однородные и неоднородные системы.

Система линейных уравнений с переменными имеет вид: 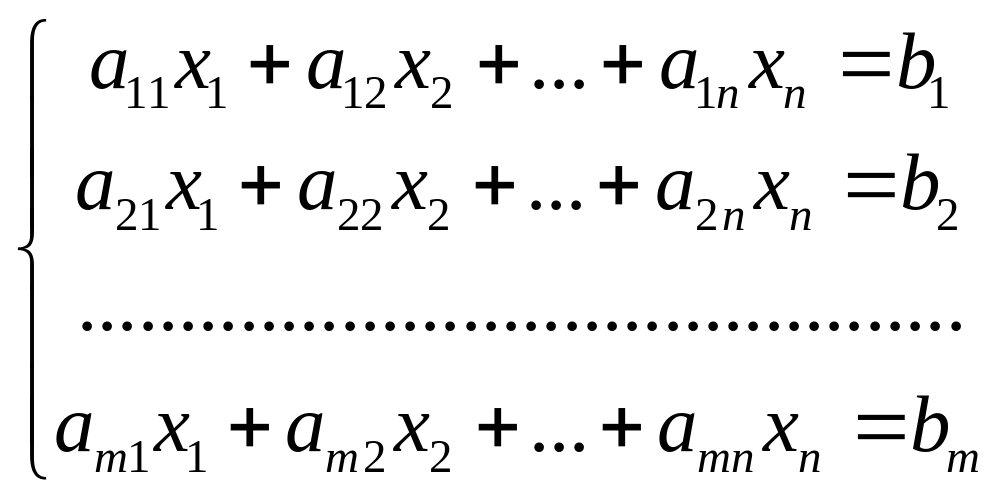, где - произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

Решением системы называется такая совокупность чисел ( , , …, ), при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Система линейных уравнений с переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид: .

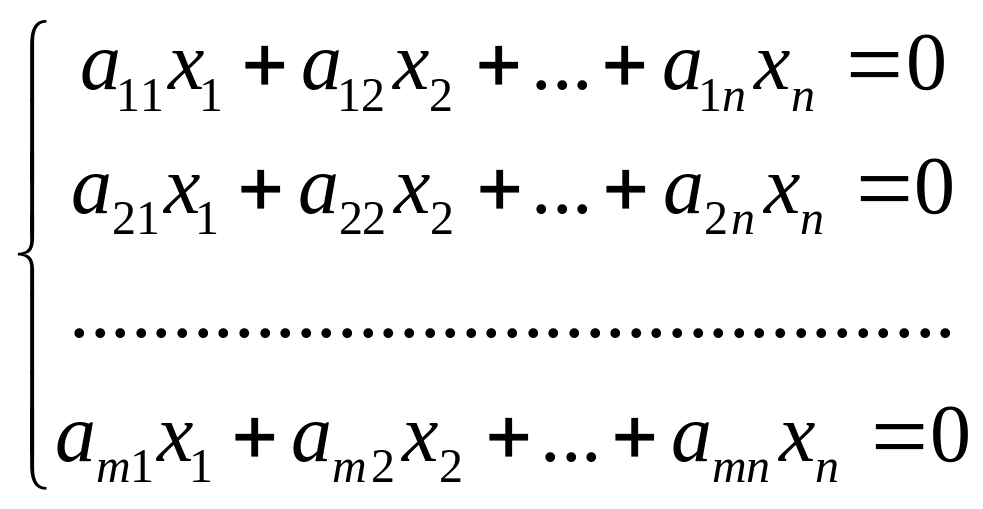Определение. Система линейно независимых решений называется фундаментальной, если каждое решение системы является линейной комбинацией решений .

Теорема. Если ранг матрицы коэффициентов при переменных системы линейных однородных уравнении меньше числа переменных , то всякая фундаментальная система решений состоит из решений.