
- •Лекция 1 Основные принципы излагаемого подхода к теории систем
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Логическое объединение качественных целей.
- •Поиск эффективных точек
- •Принцип Оптимальности
- •Формальное определение
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2 и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •Аналог игры
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
В предыдущем разделе было показано на примерах, что дополнительная информация может привести к увеличению выигрыша игрока.
Подчеркнем, что ценность полученной информации определяется не ее объемом, а полезностью. Для одних задач (целей) полезная информация одна, для других – другая. Таким образом, оценка получаемой информации определяется через функцию выигрыша.
Далее будет показано, как формализовать информированность в виде стратегий и что это дает с точки зрения принятия решения и даже для определения самого понятия решения.
Информационное расширение игры
Пусть задана исходная игра Г=<X1, X2, M1, M2>, тогда игра
I=<X1,X2,π,M1(x1,x2),M2(x1,x2)называется
информационным расширением игры
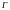 ,
если существует проекция π:
,
если существует проекция π:
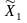 ×
×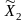
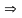 X1×X2,
обладающая следующими свойствами:
X1×X2,
обладающая следующими свойствами:
1) Каждой паре стратегий (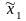 ,
,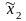 )
×
ставит в соответствие пару управлений
(исходов) (x1, x2)
X1×X2
)
×
ставит в соответствие пару управлений
(исходов) (x1, x2)
X1×X2
2) Множество стратегий
 содержит стратегии
содержит стратегии
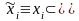
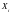 ,
т.е. стратегии – управления, не использующие
информации.
,
т.е. стратегии – управления, не использующие
информации.
3) Функции выигрыша в игре
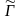 вычисляются по правилу:
вычисляются по правилу:
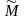 i(
i(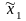 ,
,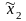 ) = Mi(π
(
,
))
) = Mi(π
(
,
))
Не для любых множеств стратегий выполняется свойство (1), а следовательно и свойства (2) и (3).
Например, возьмем пару {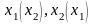 }.
В этом случае игрок 1 знает о выборе
второго, а игрок 2 одновременно знает
выбор первого - противоречие. Следовательно,
пара {
}
«физически» не реализуема.
}.
В этом случае игрок 1 знает о выборе
второго, а игрок 2 одновременно знает
выбор первого - противоречие. Следовательно,
пара {
}
«физически» не реализуема.
Свойство (2) заключается в следующем:
Игроки могут использовать стратегии, для выбора которых не требуется учета информации, но это, как правило, нецелесообразно (приводит к потере выигрыша).
Выигрыши в игре определяются по свойству (3) равенством:
i( , ) = Mi( π ( , ))
Т.е. сначала стратегии (
,
)
проектируются во множество управлений
(исходов) - (x1, x2)
X1×X2,
а затем вычисляются значения
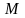 i(
i(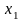 ,
), как и в игре Г.
,
), как и в игре Г.
Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
Пример
1:
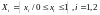
Пусть
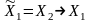 ,
т.е.
,
,
т.е.
,
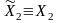 ,
т.е.
,
т.е.
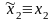
Тогда
(
,
)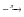
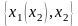 .
.
Фиксируем для примера:
X1=x(x2)=x2^2
X2=x2=1/2.
Тогда эти стратегии проектируются так:
( x 1, x 2 ) ( x 1 (x 2 ) , x 2 ) (x 2/2, ½) =(1/4,1/2)
Пример 2:
Пусть x1: x 2 X 1 т.е. ,
x
2 : x
1X
2, т.е.
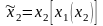 - игрок 2 принимает решение в зависимости
от стратегии первого игрока. Например,
- игрок 2 принимает решение в зависимости
от стратегии первого игрока. Например,
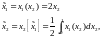
Проектируем:
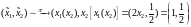 ,
,
так как
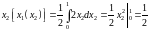 .
.
Ситуация равновесия по Нэшу в информационном расширении игры
Пусть задана игра:
Г = <
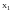 ,
,
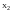 ,
,
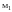 ,
,
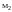 >
>
и ее информационное расширение:
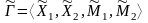
Определение.
(
0,
0)-
ситуация равновесия в информационном
расширении игры, если M10
=M1(π(
0,
0))=
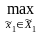 M1(π(
,
0))
M1(π(
,
0))
M20=
M2(π(
0,
0))=
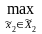 M2(π(
0,
)
M2(π(
0,
)
Заметим ,что
( 0,
0)
π (х10, х20) –
равновесный исход, но не ситуация
равновесия!
0,
0)
π (х10, х20) –
равновесный исход, но не ситуация
равновесия!
Таким образом, ситуация равновесия может реализоваться на стратегиях
(
º,
º)
є
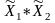
но ее проекция
( хº1, хº2) є
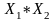
не обязательно равновесная по Нэшу.
Напомним, что стратегия а = х1а(х2) называется абсолютно оптимальной стратегией, если справедливо равенство:
M1(x1а(x2),
x2)=
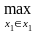 M1(x1,
x2)
M1(x1,
x2)
Определим x2= х2а - оптимальный ответ второго игрока из условия:
M2(x1а(x2), x2) = M2(x1а(x2а), x2а )
Положительные свойства стратегий:
Свойство 1.
Ситуация равновесия всегда существует на классе стратегий
( , )=(x1(x2), x2)
Доказательство: Достаточно выбрать абсолютно оптимальную стратегию а = хª1(x2), и оптимальный ответ на нее а = х2а
По определению:
M1(x1а(x2),
x2) =
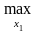 M1(x1,
x2),
M1(x1,
x2),
M2(x1а(x2а), x2а ) = M2(x1а(x2), x2).
Тогда, если = х2а, то
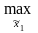 M1(π(
,x^2а))=
M1(x1(xª2),
xª2)
= M1(x1а(x2а),
x2а
).
M1(π(
,x^2а))=
M1(x1(xª2),
xª2)
= M1(x1а(x2а),
x2а
).
Если
=
а
(
),
то
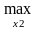 M2(x1а(x2),
x2 )=
M2(x1а(x2а),
x2а), что
соответствует определению ситуации
равновесия в информационном расширении
игры.
M2(x1а(x2),
x2 )=
M2(x1а(x2а),
x2а), что
соответствует определению ситуации
равновесия в информационном расширении
игры.
Свойство 2.
Если
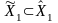 ,
то и
,
то и
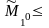
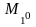 –
увеличение информации приводит к
возможности увеличения выигрыша.т
–
увеличение информации приводит к
возможности увеличения выигрыша.т
Доказательство:
Первый игрок может не использовать
дополнительную информацию и получить
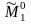 .
А если повезёт (дополнительная информация
оказалась полезной), то получит строго
больше.
.
А если повезёт (дополнительная информация
оказалась полезной), то получит строго
больше.
Свойство 3.
Пусть игрок 1 знает х2 .
Определим взаимовыгодное множество для этого случая:
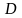 12={(х1,
х2)
M1(
х1, х2) ≥
12={(х1,
х2)
M1(
х1, х2) ≥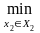
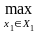 M1(х1, х2);
M1(х1, х2);
M2( х1, х2)
≥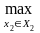
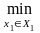 M2(х1,
х2)}.
M2(х1,
х2)}.
Любая точка из этого множества может быть сделана ситуацией равновесия на классе стратегий
{х1(х2), х2[х1(х2)]}
Аналогичное утверждение верно и в симметричном случае, когда игрок 2 знает х1.
Здесь взаимовыгодное множество определяется следующим образом:
21={(х1,
х2)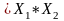 M1(
х1, х2) ≥
M1(х1,
х2);
M1(
х1, х2) ≥
M1(х1,
х2);
M2( х1, х2) ≥ M2(х1, х2)}.
А класс использованных стратегий имеет вид:
{ х1 [х2(х1)], х2 (х1)}.
Для иллюстрации сделанных выводов рассмотрим следующий
Пример. [1]
Исследуем биматричную игру:
М1=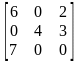 M2=
M2=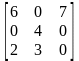
Сначала найдем равновесные ситуации в исходной игре.
Для этого определим:
x1a(x2) –абсолютно оптимальную стратегию первого игрока и
х2 = x2a – оптимальный ответ второго.
Напомним, что:
x1a(x2): M1(x1a(x2), x2) = M1(x1, x2)x2a:
M2(x1a(x2а), x2a) = M2(x1a(x2а), x2).
Итак:
 3, если x2
= 1
3, если x2
= 1
x1a(x2) = 2, если x2 = 2
 2, если x2
= 3
2, если x2
= 3
Аналогично: 3, если x1 = 1
x2a(x1) = 2, если x1 = 2
2, если x1 = 3
Единственная ситуация равновесия в исходной игре определяется из условия пересечения оптимальных стратегий в точке (x1a(x2а) , x2a(x1a)) (2,2).
В этой ситуации выигрыши игроков равны (4,4).
Построим П-множество Парето на классе исходных управлений.
Напомним, что
(x1п, x2п) П
если не существует (x1', x2')єХ1*Х2, такой что:
Mi(x1', x2') ≥ Mi(x1п, x2п), i=1, 2 (дизъюнкция)
Mi(x1', x2') > Mi(x1п, x2п), i=1 либо i=2 (конъюнкция)
В пространстве выигрышей множество возможных решений имеет вид:
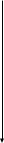
M2
П
 7
7
6 П
4 (4, 4) с.р.
3
2 П

0 2 3 4 6 7 M1
рис.1
Как видно из рис.1:
П = {( 1,1); (1,3); (3,1)},
С выигрышами игроков соответственно
МП = {(6,6); (2,7); (7,2)}.
Непосредственной проверкой убеждаемся, что ни одна из этих точек не является ситуацией равновесия в исходной игре.
Покажем, что эти ситуации могут быть результатом проекции равновесных стратегий вида:
{ х1(х2), х2[х1(х2)]}, {х1[х2(х1)], х2(х1)}.
Имеем для игрока 1:
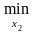 M1(x1,
x2) = 0
M1(x1,
x2) = 0
M1(x1, x2) = 3
Определим: х2 = х2H - стратегия наказания первого игрока вторым, из условия
M1(х1, х2) = M1(х1, х2H)
В данном случае имеем х2H=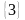 .
.
Далее для игрока 2 имеем:
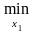 M2(x1, x2)
= 0
M2(x1, x2)
= 0
M2(x1, x2) = 3
Определим х1H (х2) - стратегию наказания второго игрока первым.
2, если х1 = 1
х1H (х2)= 1, если х2 = 2
3 (2), если х3 =3
Покажем, что равновесные стратегии можно выбрать на классе стратегий {x1(x2), x2 [x1(x2)]} .Действительно , пусть
 x10
(x2)
= 1, х2=1
0
= х20
[х1(х2)]
= 1,
=
x10
(x2)
= 1, х2=1
0
= х20
[х1(х2)]
= 1,
=
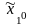
х1н (х2), х2 1 , х2н = 3,
Очевидно, эти стратегии проектируются в точку (х1 = 1, х2=1). В этой точке M1 = 6, M2 = 6.
Если от этих стратегий отклонится игрок 1, то есть , то он получит не больше, чем
M1(π( , 0))= M1(π ( , 3) = M1(2, 3) = 3 < 6.
Таким образом, игроку 1 не выгодно отклоняться от точки ( , 0).
Если же при
=
,
игрок 2 выберет
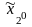 ,
то его выигрыш оценивается величиной
,
то его выигрыш оценивается величиной
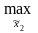 M2[π(
0,
)].
M2[π(
0,
)].
Если т.ч. х2 1, при = , то
M2[π( 0, )] = M2(х1H(х2), х2) = 0 < 6
Итак, игроку 2 также не выгодно отклоняться
от точки (
,
0),
то есть (
,
0)
– ситуация равновесия в игре
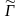 .
.
Замечание. Точку из множества Парето можно сделать равновесной, если выигрыши игроков в ней оцениваются величиной не меньшей, чем их максимально гарантированные результаты, соответствующие их информированности. Этому условию удовлетворяют также точка (7,2) на классе стратегий {x1(x2), x2 [x1(x2)]} и точка (2,7) на классе стратегий {x2(x1), x1 [x2(x1)]}.
Упражнение.
Точку (7,2) можно сделать ситуацией равновесия на классе
{x1(x2), x2 [x1(x2)]}
Точку (2,7) можно сделать ситуацией равновесия на классе
{x2(x1), x1 [x2(x1)]}.
Итак, для построения ситуаций равновесия в игре двух лиц на сложных стратегиях необходимо проделать следующее:
Вычислить гарантированные (минимальные или максимальные, в зависимости от информированности ) результаты игроков.
Определить стратегии наказания, применение которых не позволит партнеру получить выигрыш, превышающий его гарантированный результат.
Определяется множество взаимовыгодных исходов, на котором игроки получают выигрыш, не меньший гарантированного результата.
Путем переговоров выбирается точка из этого множества, устраивающая обоих партнеров.
С помощью простой процедуры конструируются равновесные стратегии, включающие в себя обязательства выбора договорного исхода и штрафы на основе стратегий наказания за нарушение договоренностей.
Таким образом, решение сложнейшей по постановке задачи оказывается не сложнее, а. как правило, значительно проще решения традиционной задачи поиска ситуации равновесия. При этом построение взаимовыгодного множества дает полное решение задачи - построить все ситуации равновесия!
Проведем анализ рассмотренных ранее иллюстративных игр, но уже на классе стратегий.
Игра «продавец – покупатель»
В этой игре на классе исходных управлений не существует равновесной ситуации.
Пусть теперь например, покупатель имеет информацию о действиях продавца. Тогда его абсолютно оптимальная стратегия заключается в доверии (без затрат на проверку в случае честного поведения продавца. Если же продавец обманул, то оптимальное поведение покупателя – проверить и наказать продавца. Оптимальный выбор продавца в этой ситуации –честно взвесить товар. Что приводит к исходу – (честно взвеситл, поверил). Подчеркнем, что эта ситуация не является ситуацией равновесия в исходной игре! Ситуация равновесия реализуется только на классе стратегий.
Аналогично, если продавец знает выбор покупателя, то его абсолютно оптимальная стравтегия заключается в честном поведении при угрозе проверки - и обмане – в случае доверчивого покупателя. Оптимальный ответ покупателя на эту стратегию – проверять продавца. В этом случае реализуется исход –(честно взвесил, проверил), котороый опять же не является равновесным в исходной игре.
Заметим, что различные варианты информированности приводят к различным ситуациям равновесия.
Игра «семейный спор»
В этой игре существуют две неравноценные для партнеров ситуации равновесия: идти вместе на футбол или идти вместе на балет. Эта игра на классе стратегий хорошо иллюстрирует тот факт, что иногда более важно владеть инициативой, а не информацией. Кто из партнеров первым ходит, то есть первым делает выбор и сообщает о нем партнеру, тот и добивается для себя более выгодной ситуации равновесия. Если главенствует муж, то жене придется идти с ним на футбол. Если муж находится «под каблуком», то он обречен ходить на балет.
Заметим, что в дружной семье главенствующий всегда идет на компромисс, предлагая поочередно наслаждаться балетом и футболом. Однако в этой ситуации мы выходим за рамки статической модели, определяя интегральный (осредненный по времени) выигрыш в динамической модели повторящейся игры.
Игра «реклама»
В этой игре существует единственная ситуация равновесия – обоим партнерам рекламировать свой товар. Однако существует более эффективный для обоих партнеров вариант, оптимальный по Парето, - не тратиться на рекламу. Но эта ситуация не является равновесной на классе исходных управлений. Однако эта ситуация принадлежит взаимовыгодному множеству, а значит ее можно сделать результатом проекции равновесных стратегий, включающих в себя договорные обязательства со штрафами за отклонение от них.
