Тема 6. Непрерывные случайные величины

Случайная величина X называется непрерывной случайной величиной, если её функция распределения (интегральная функция распределения) представима в виде

,

где f(x) – некоторая неотрицательная функция, такая что .

Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).

Примеры непрерывных распределений

1. Равномерное распределение (a<b)

.

2. Нормальное распределение (>0)

3. Показательное распределение (>0)

Математическим ожиданием непрерывной случайной величины X называется число ; если все возможные значения Х принадлежат интервалу (а,b), то .

Дисперсия D(X) непрерывной случайной величины вычисляется по формуле или ; если все возможные значения Х принадлежат интервалу (а,b), то или

Вероятность того, что случайная величина X принимает значение в заданном промежутке, вычисляется по одной из формул:

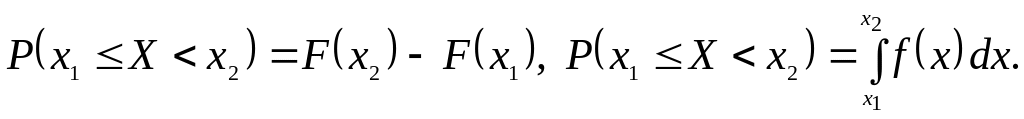
Пример 17. (Варианты 2, 3, 4, 6, 7)

Случайная величина задана плотностью вероятности

Найти: а) параметр а;

б) функцию распределения F(x);

в) вероятность попадания X в интервал .

Построить графики f(x), F(x).

Решение:

а) Для нахождения параметра а воспользуемся свойствами функции f(x):

1) 2)

Из первого следует, что a 0, а из второго определяется конкретное значение а.

,

б) Для нахождения функции F(x) используем равенство

Так как f(x) задана различным образом на трёх разных интервалах, то выражение для F(x) находим отдельно для каждого из них.

Если то

Если то

Если то .

Искомая интегральная функция принимает вид

в) Вероятность попадания случайной величины X в интервал .

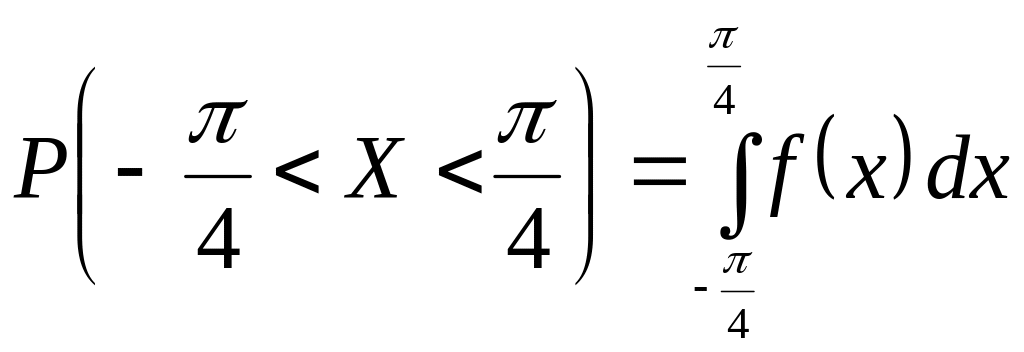или

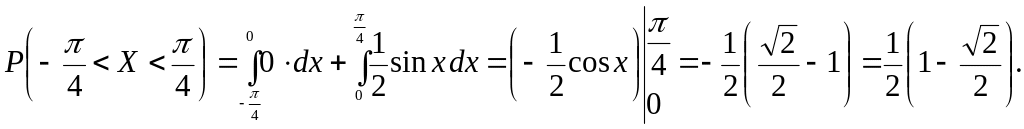
Искомая вероятность может быть найдена иначе

Г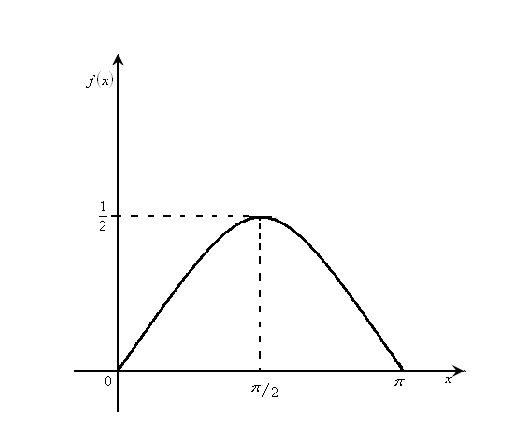 рафики функций f(x) и F(x) показаны соответственно на Рис. 3 и Рис. 4.

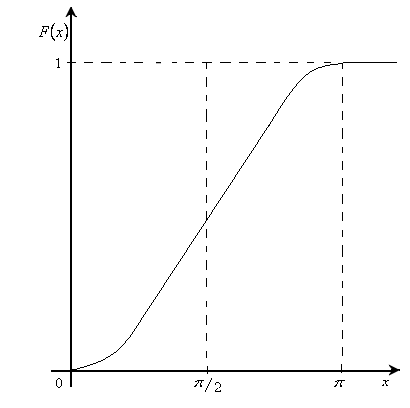
Рис. 3 Рис.4

Пример 18. (Варианты 1, 5, 8, 9, 10)

Дана функция распределения непрерывной случайной величины X

Найти: а) плотность распределения f(x);

б) параметр а;

в) математическое ожидание M(X).

Решение:

а) Плотность распределения равна первой производной от функции распределения:

(При х=0 производная не существует, т.к. левая и правая производные в этой точке неравны друг другу).

б) Для нахождения параметра а пользуемся свойствами функции f(x):

, .

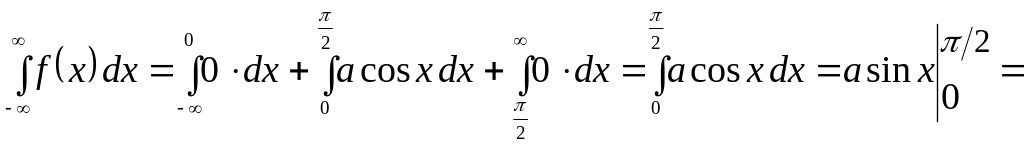
Значит,

в)

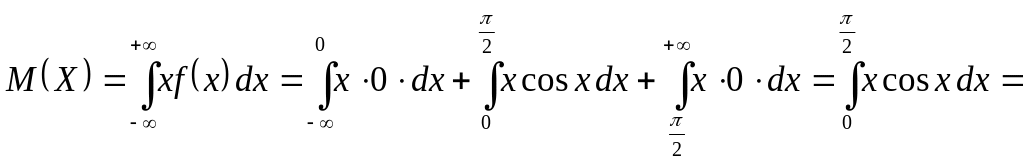
Тема 7. Равномерный и показательный законы распределения

1. Равномерным называется распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид

Это значит, что f(x) сохраняет постоянное значение на [a; b].

Функция распределения равномерного закона

Вероятность попадания в интервал (x₁; x₂) непрерывной случайной равномерно распределенной величины X

P(x₁<X<x₂)= .

Математическое ожидание, дисперсия и среднее квадратическое отклонение равномерного распределения:

2. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

где  - постоянная положительная величина.

Функция распределения показательного закона

Вероятность попадания в интервал (a, b) непрерывной случайной величины X, распределенной по показательному закону,

P(a<X<b)=

Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения:

Пример 19. (Варианты 2,3)

Цена деления прибора равна 0,1. Показания прибора округляются до ближайшего целого. Найти: а) вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02; б) M(X), D(X), (X), если случайная величина X – ошибка округления.

Решение: Ошибку округления рассматриваем как случайную величину X, равномерно распределенную между двумя соседними целыми делениями.

Тогда плотность распределения где b-a – длина интервала распределения значений X; вне этого интервала f(x)=0.

b-a=0,1 (цена деления прибора), поэтому

Ошибка отсчета превысит 0,02, если X попадает в интервал (0,02;0,08).

P(x₁<X<x₂)= или P(x₁<X<x₂)= .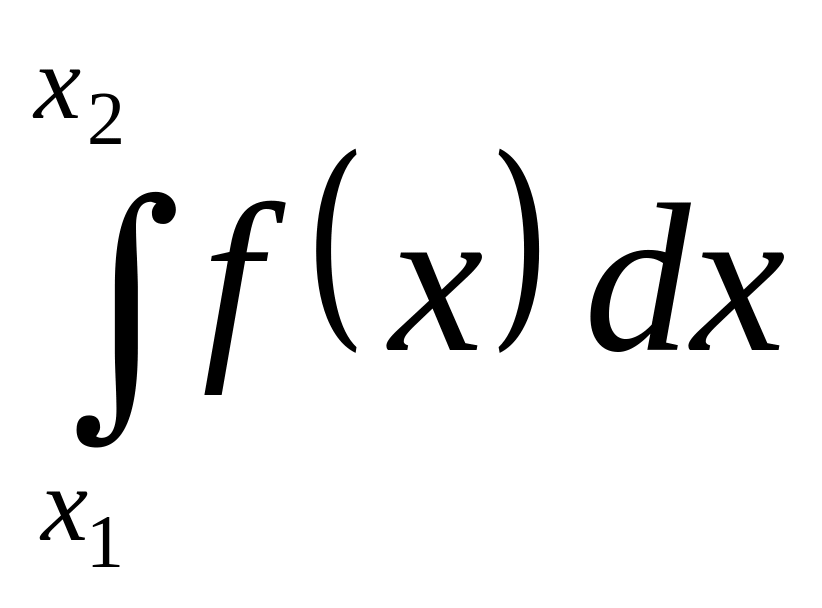

P(0,02<X<0,08)=

Математическое ожидание X (считаем a=0, b=0,1)

.

Дисперсия

Среднее квадратическое отклонение

Пример 20. (Варианты 1,4,5,6)

Автобусы идут строго по расписанию. Интервал движения 7 минут. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут; в) математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания пассажира.

Решение: Время ожидания пассажира рассматриваем как случайную величину X, равномерно распределенную между приходами двух автобусов.

По условию задачи длина интервала распределения значений X b-a=7,

здесь b=7, a=0.

а) Время ожидания будет менее двух минут, если X попадает в интервал (5;7).

P(x₁<X<x₂)= ; P(5<X<7)=

б) Время ожидания будет не менее трех минут, если X попадает в интервал (0;4).

P(0<X<4)=

в) Математическое ожидание .

Среднее квадратическое отклонение

Пример 21. (Варианты 7, 8, 9, 10)

Показательное распределение задано при плотностью f(x)=5e ^-5x. Требуется: а) записать выражение для функции распределения; б) найти вероятность того, что в результате испытания X попадает в интервал (1, 4); в) найти вероятность того, что в результате испытания ; г) вычислить M(X), D(X), (X).

Решение:

В данной задаче =5

а)

б)

в) , значит a=2, b= , т. е.

(т.к. )

г) для показательного распределения