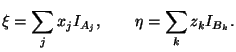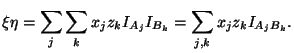2.8 Независимость случайных величин

Определим понятие независимости для дискретных случайных величин.

Определение 2.6 Случайные величины называются независимыми, если для всех

Другими словами, набор есть набор независимых событий.

Упражнение 2.8 Показать, что события независимы тогда и только тогда, когда случайные величины взаимно независимы.

Предложение 2.4 Предположим, что

1. независимые случайные величины,

2. существуют математические ожидания .

Тогда

Доказательство. Для простоты рассмотрим лишь случай . Обозначим , . Пусть и имеют следующие распределения:

Обозначим

Имеют место представления

(9)

Заметим, что . Следовательно,

(10)

Аналогично Замечанию 2.7, при любом фиксированном в бесконечных суммах (9) содержится не более одного ненулевого слагаемого, так что с произведением рядов в (10) нет никаких проблем.

Так как , если , то мы можем воспользоваться доказанной выше Леммой 2.2:

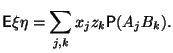
Так как и независимы, то

Следовательно,

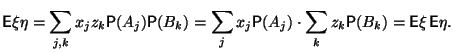
Предложение доказано.

Следствие 2.1 Если и независимы, то

Доказательство.

Действительно, по предложению в силу независимости и . С другой стороны, (см. Упражнение 2.7). Отсюда утверждение следствия легко следует.

2.9 Некоррелированность случайных величин

Определение 2.7 С.в. и называются некоррелированными, если

Замечание 2.8 Соотношение между независимостью и некоррелированностью случайных величин можно записать в виде следущей диаграммы:

Независимость		некоррелированность

Прямая импликация была установлена нами в Следствии 2.1. Пример некоррелированных, но зависимых случайных величин будет приведен позже, в 4.4.

Таким образом, если ковариация отлична от нуля, то это свидетельствует о зависимости случайных величин. Для того, чтобы иметь количественный показатель того, насколько сильно зависят друг от друга случайные величины, часто используют коэффициент корреляции:

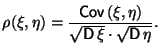
Оказывается, что всегда

Это можно доказать, применяя хорошо известное неравенство Коши-Буняковского (см. [1, Предложение 7.12]).

Более того, из этого неравенства вытекает, что если , то случайные величины и линейно зависимы:

Замечание 2.9

Линейная зависимость случайных величин и или, что то же самое, их коллинеарность являются частным случаем их функциональной зависимости, то есть зависимости вида , где -- некоторая (необязательно линейная) функция двух вещественных переменных. Из вышесказанного следует, что коэффициент корреляции хорошо отражает степень линейной зависимости между случайными величинами. Вместе с тем, позже мы покажем, что коэффициент корреляции может быть совершенно ``нечувствителен'' к функциональной зависимости (см. Замечание 4.2).

Следствие 2.2 Если независимы, то

Вытекает из п. 3) Предложения 2.2 и Следствия 2.1.

Пример 2.7 Рассмотрим вероятностное пространство , определенное формулами (2) и (3), соответствующее последовательности из независимых испытаний Бернулли. Введем случайные величины:

Можно проверить, что -- независимы и имеют бернуллиевское распределение

Число успехов в последовательности независимых испытаний (см. Пример 2.2) можно записать в виде Тогда