Применение предикатов в алгебре

Рассмотрим предикаты, в которых свободной является лишь одна пе­ременная, которую обозначим через х, и обсудим применение предикатов в алгебре.

Типичным примером является уравнение, например, х² - 3х + 2 = о.

Свободная переменная может принимать здесь любое числовое значение. Для некоторых чисел х (а именно х = 1, х = 2) утверждение, содержа­щееся в этом уравнении, истинно, в остальных оно ложно. В подобных случаях, когда истинность или ложность предиката зависит только от значения, принимаемого свободной переменной х, множество допусти­мых значений х можно рассматривать как множество логических воз­можностей U, а множество всех значений этой переменной, при которых высказывание истинно - как его множество истинности.

В приведенном выше примере множество U состоит из всех действи­тельных чисел, а множеством истинности является множество {1, 2}.

В результате введения понятия множества истинности для предика­тов можно сказать, что решить уравнение - значит найти один эле­мент или все элементы его множества истинности. При решении системы двух уравнений у нас имеется предикат, представляющий конъюнкцию двух уравнений. Поэтому мы ищем пересечение двух множеств истинно­сти. Если это пересечение пусто, то система уравнений не имеет решений. Такие уравнения называются несовместнымu, поскольку их множества истинности не имеют общих элементов х.

Понятие множества истинности удобно не только в вопросах, связан­ных с решением уравнений, но и при рассмотрении неравенств.

Если U - множество действительных чисел, то множество истинно­сти нера-венства х < 0 состоит из всех отрицательных действительных чисел. Множество же истинности неравенства х > -3 состоит из всех действительных чисел, больших, чем -3. Если мы потребуем, чтобы эти неравенства выполнялись одновременно, то множеством истинности бу­дет множество, являющееся пересечением двух исходных множеств, т. е. все действительные числа между - 3 и 0.

Понятие множества истинности предиката позволяет выяснить, чем разнятся между собой уравнения и тождества. Когда мы решаем уравне­ние, мы тем самым ищем один из элементов множества истинности этого уравнения или все его элементы. Если же мы доказываем тождество, то тем самым утверждаем, что оно справедливо для всех х. Таким обра­зом, тождество представляет собой уравнение, множеством истинности которого является универсальное множество U, т. е. является логически истинным или тождественно истинным.

Так как к предикатам можно применять логические операции, для них справед-ливы основные законы булевой алгебры.

Кванторы

Помимо операций алгебры высказываний, в логике предикатов есть две операции, которые связаны с природой предикатов. Пусть дан преди­кат Р(х), зависящий от одной переменной и определенный на поле М.

а) Выражение ( x)P(x) означает высказывание, истинное только в том случае, когда предикат Р( х) истинен для всех предметов из поля М. Выра­жение ( x)P(x) читается «для всякого х, Р(х)», здесь символ ' ' - квантор общности.

б) Выражение (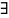 х)Р(х) означает высказывание, истинное только в том случае, когда предикат Р(х) истинен хотя бы для одного предмета из по­ля М. Выражение ( х)Р(х) читается «существует х, что Р(х»); символ ­ - квантор существования .

Рассмотрим примеры применения операций квантирования к преди­катам. Пусть даны предикаты над полем натуральных чисел:

1) х² = х· х, тогда ( x)(x² = х· х) - истинное высказывание;

2) х + 2 = 7, тогда ( x)(x + 2 = 7) - ложное высказывание; а ( х)(х + 2 = 7) - истинное высказывание;

3) х + 2 = х, тогда (' x)(x + 2 = х) - ложное высказывание.

Квантор общности - это оператор, приводящий в соответствии лю­бому заданному предикату y = Р(х) такую двузначную логическую пере­менную z, которая принимает значение 1 тогда и только тогда, когда у = 1 при всех значениях х.

Квантор существования - это оператор, приводящий в соответствии любому одноместному предикату y = Р(х) такую двузначную логическую переменную z, которая принимает значение 0 тогда и только тогда, когда у = 0 при всех значениях х.

Рассмотрим некоторые общие свойства введенных операторов.

В соответствии с определениями кванторов логическая переменная z в выражениях

z = ( x)P(x) z = ( х)Р(х)

уже не является функцией предметной переменной х.

Для того чтобы отметить отсутствие функциональной зависимости z от х, предметную переменную х в таких случаях называют связанной. Несвязанные переменные называют свободными.

Например, в предикате

( x)A(x, у) ˅ ( z)B(z, v)

переменные х и z - связанные, а у и v - свободные.

Если квантор общности или квантор существования применяется не к одно-местному предикату, а к какому-нибудь k-местному предикату, то в результате этого получается снова предикат, но за счет связывания одной предметной переменной получаемый предикат будет (k - l)-местным.