1.1.2 Применение метода контурных токов

Метод контурных токов основан на использовании второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.

В заданной цепи (рисунок 1.1) можно рассмотреть три контура-ячейки (ACBA, ADCA, CDBC) и ввести для них контурные токи Ik1, Ik2, Ik3.

Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

• стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках. Направление обхода контуров принимаем таким же;

• составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.

I k1(R1 + r01 + R3 + R5) – Ik2(R1 + r01) – Ik3R5 = -E1

-Ik1(R1 + r01) + Ik2(R1 + r01 + R4 + R6) – Ik3R6 = E1

-Ik1R5 – Ik2R6 + Ik3(R2 + r02 + R5 + R6) = -E2

П одставляем в уравнение численные значения ЭДС и сопротивлений.

102∙Ik1 – 53∙Ik2 – 25∙Ik3 = -40

-53∙Ik1 + 113∙Ik2 – 42∙Ik3 = 40

-25∙Ik1 – 42∙Ik2 + 102∙Ik3 = -30

Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆1, ∆2, ∆3.

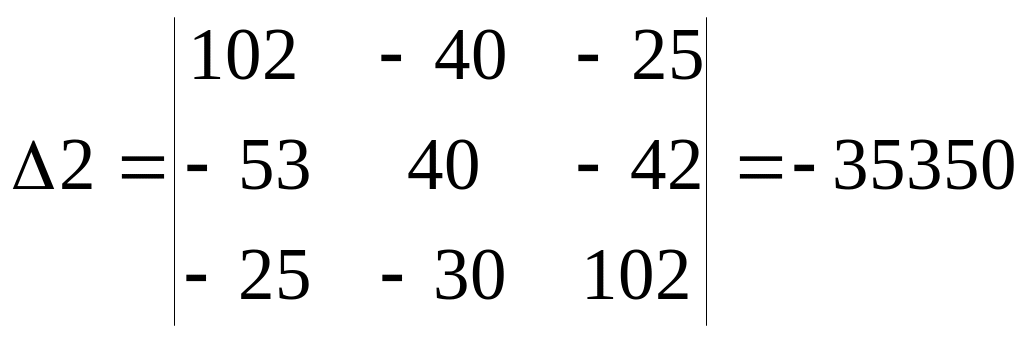
Вычисляем контурные токи:

A; A;

A;

Действительные токи ветвей:

I1 = Ik2 – Ik1 = -0.067 – (-0.538) = 0.471 A;

I2 = -Ik3 = 0.454 A;

I3 = -Ik1 = 0.538 A;

I4 = -Ik2 = 0.067 A;

I5 = Ik3 – Ik1 = -0.454 – (-0.538) = 0.085 A;

I6 = Ik2 – Ik3 = -0.067 – (-0.454) = 0.387 A.

1.1.3 Применение метода наложения.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

а) Определяем частные токи от ЭДС Е2 при отсутствии ЭДС Е1, т. е. рассчитываем цепь по рисунку 1.2. Решаем задачу методом «свертки».

R101 = R1 + r01 = 52 + 1 = 53 Ом

В заданной электрической цепи сопротивления R3, R5 и R101 соединены в треугольник, который для упрощения преобразуем в звезду.

Определяем сопротивления:

Ом

Ом

Ом

R2A = R2 + RA = 39.882 Ом

R6C = R6 + RC = 54.990 Ом

R4B = R4 + RB = 30.471 Ом

Ом

Rэ = R4B6C + R2A = 59.489 Ом

Ток источника

А

Вычисляем остальные токи ветвей:

А

А

А

А

А

Рисунок 1.2 − Схема линейной электрической цепи

постоянного тока без источника ЭДС E1

б) Определяем частные токи от ЭДС Е1 при отсутствии ЭДС Е2, т.е. рассчитываем простую цепь по рисунку 1.3.

Решаем задачу методом «свертки».

R202 = R2 + r02 = 34 + 1 = 35 Ом

В заданной электрической цепи сопротивления R5, R6 и R202 соединены в треугольник, который для упрощения преобразуем в звезду.

Определяем сопротивления:

Ом

Ом

Ом

Рисунок 1.3 − Схема линейной электрической цепи

постоянного тока без источника ЭДС E2

R4A = R4 + RA = 32.412 Ом

R3C = R3 + RC = 32.578 Ом

Ом

Rэ = R4A3C + RB + R1 = 78.541 Ом

Ток источника

А

Вычисляем остальные токи ветвей:

А

А

А

А

А

Вычисляем токи ветвей исходной цепи (рисунок 1.1), выполняя алгебраическое сложение частных токов, учитывая их направление:

I1 = I"1 – I’1 = 0.471 A; I2 = I’2 – I"2 = 0.452 A;

I3 = I’3 + I"3 = 0.538 A; I4 = I’4 – I"4 = 0.067 A;

I5 = I"5 – I’5 = 0.086 A; I6 = I’6 + I"6 = 0.385 A.