Частные случаи прямолинейного движения материальной точки

Пусть на МТ массой действует сила .

За координатную ось x выбирается прямая, вдоль которой движется точка (рис. 2.2). Возможны следующие случаи.

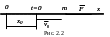1. Сила зависит от времени .

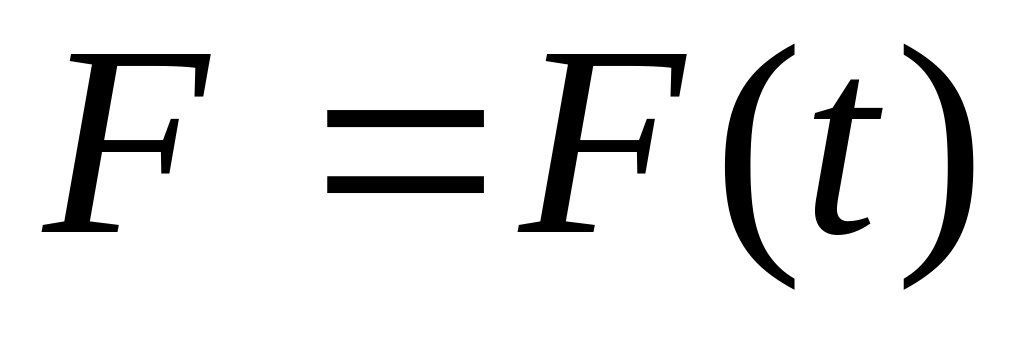Дифференциальное уравнение движения

, (2.5)

или .

Обозначив интеграл , получим

, откуда . (2.6)

Далее,

, или . (2.7)

Интегрируя второй раз, имеем

. (2.8)

Получен искомый закон движения.

2. Сила зависит от положения точки .

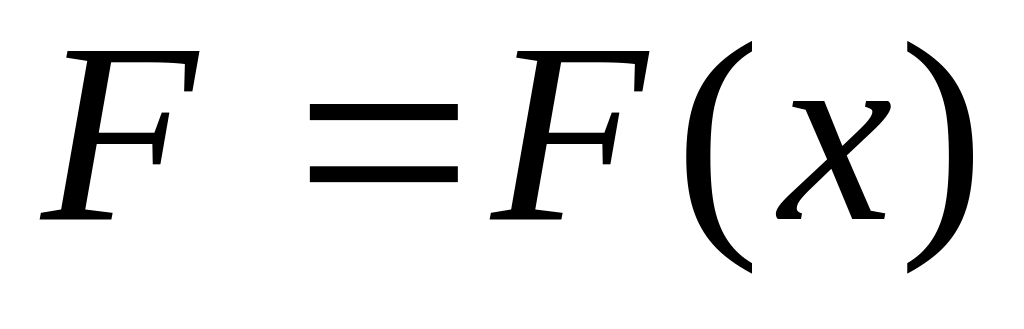Дифференциальное уравнение

. (2.9)

Представим уравнение в виде

, или . (2.10)

Находя определенный интеграл, получим

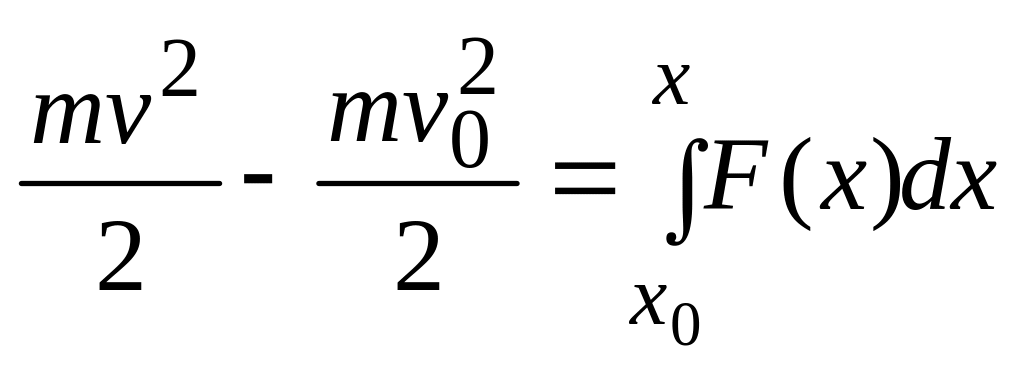. (2.11)

Обозначив 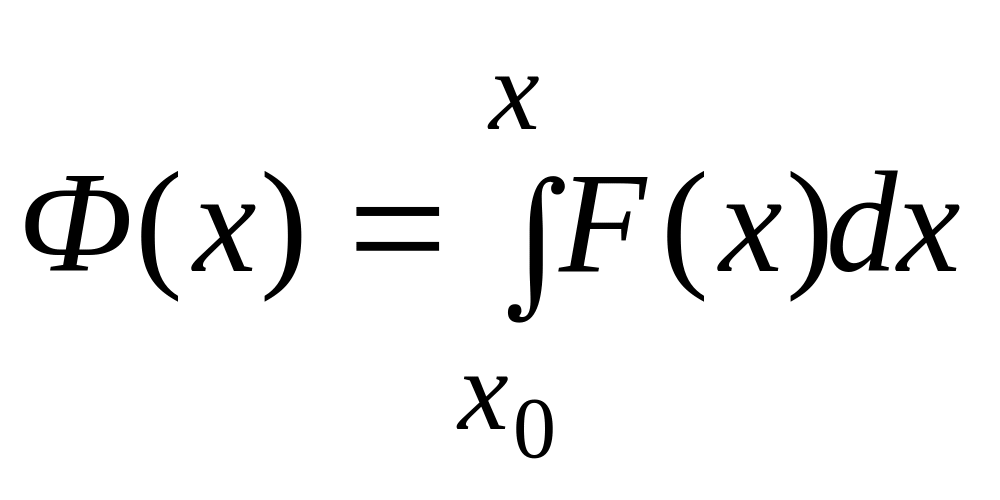, имеем,

. (2.12)

После интегрирования имеем

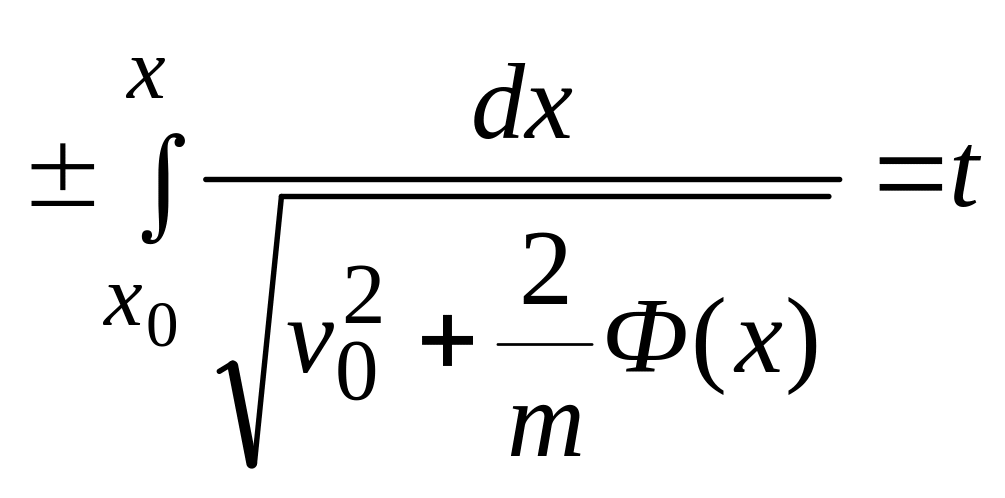, (2.13)

откуда определяется закон движения точки .

3. Сила зависит от скорости точки .

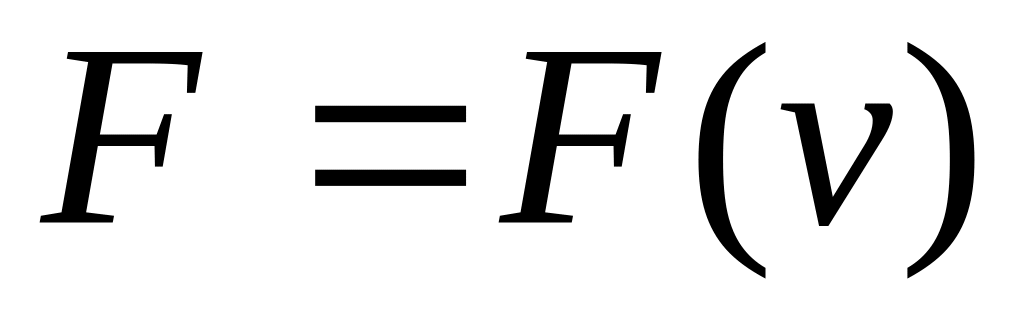Дифференциальное уравнение

. (2.14)

Возможны два способа его решения.

1-й способ. Разделим переменные

. (2.15)

После интегрирования получим

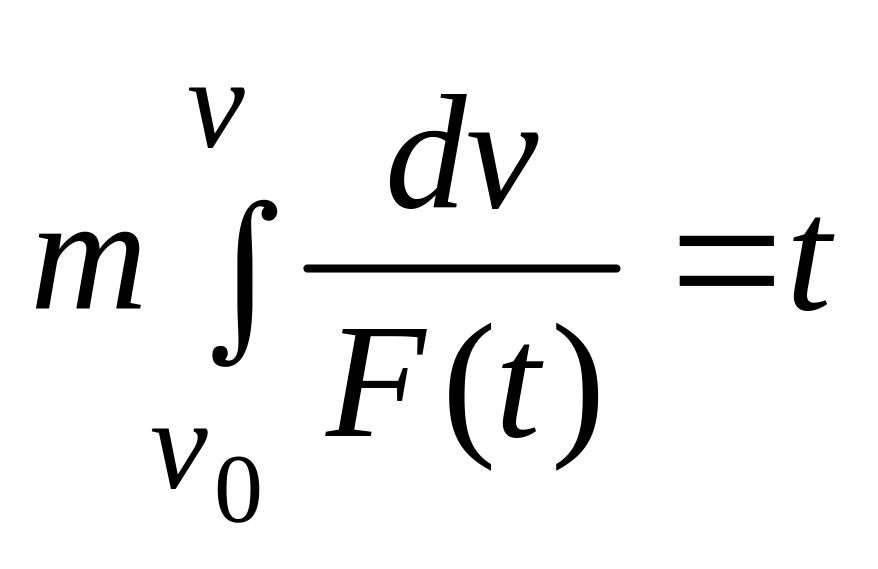, (2.16)

откуда находим зависимость скорости от времени .

Далее,

, или . (2.17)

Интегрируя второй раз, находим закон движения точки

. (2.18)

2-й способ. Напишем дифференциальное уравнение в виде

, или . (2.19)

Разделим переменные

. (2.20)

После интегрирования имеем

,

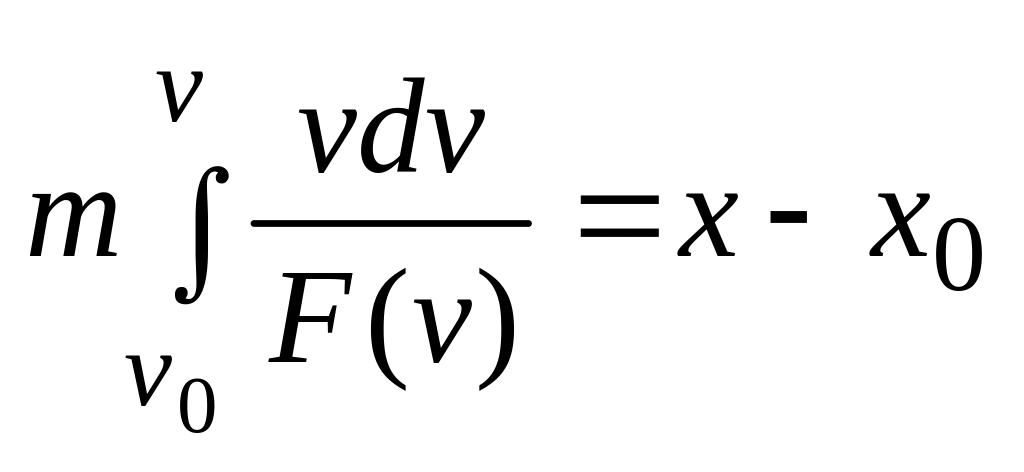откуда находим скорость как функцию координаты x

, или .

Интегрируя, получим

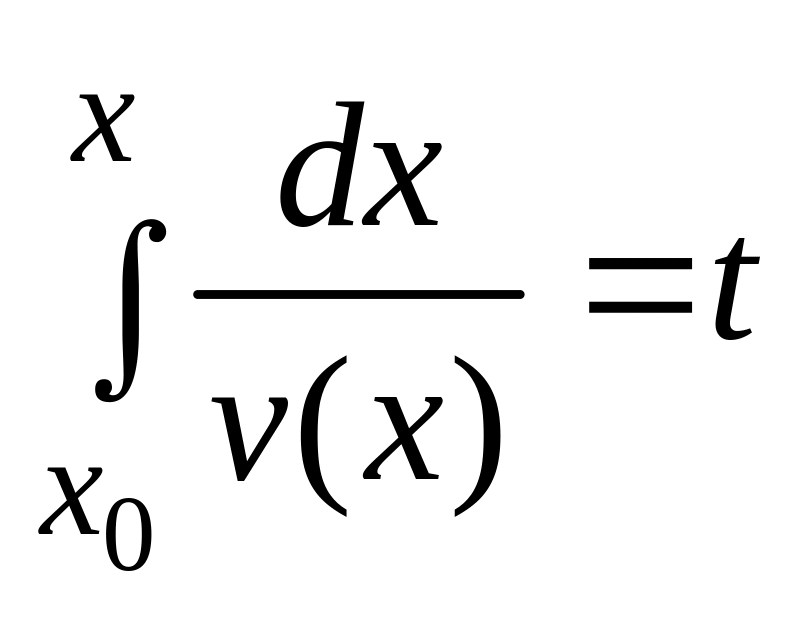, (2.21)

откуда находится закон движения .

Прямолинейные колебания материальной точки

В природе колебательное движение является широко распространенным явлением. Его изучение представляется задачей, имеющей важное практическое значение.

В зависимости от характера деформаций упругого элемента колебания различаются продольные, поперечные, изгибные, крутильные. Вместе с тем, они имеют общую природу. Это определено наличием силовых факторов, которые при отклонении системы от положения устойчивого равновесия стремятся вернуть ее в исходное положение. Предполагается, что величина каждого из этих силовых факторов прямо пропорциональна величине деформации упругого элемента, который работает в зоне линейной упругости, то есть в рамках закона Гука.

У добно в качестве упругого элемента принять пружину, работающую на продольное растяжение-сжатие. Ее упругая сила определяется выражением , где - деформация, - коэффициент жесткости пружины. Размерность , в системе СИ . Он численно равен значению силы, деформирующей пружину на единицу длины, на графике (рис. 2.3) выражается тангенсом угла наклона прямой к оси ( ).

Существует два основных вида соединения пружин: параллельное и последовательное.

При параллельном соединении двух пружин (рис. 2.4) их можно заменить одной пружиной с эквивалентным коэффициентом жесткости

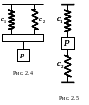
. (2.22)

Параллельным также является соединение, показанное на рис. 2.5.

При последовательном соединении (рис. 2.6) справедливо равенство

, или . (2.23)

Ф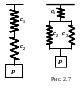 ормулы (2.22), (2.23) аналогичны соотношениям, используемым при расчетах конденсаторных цепей в электротехнике. Это обстоятельство используется при электрическом моделировании механических явлений.

Р

Рис. 2.6

асполагая этими соотношениями, можно определить коэффициент жесткости системы упругих элементов, сколь бы сложной она ни была. Например, коэффициент жесткости системы пружин при их смешанном соединении (рис.2.7) находится по формуле

, то есть . (2.24)

К олебания делятся на свободные, затухающие, вынужденные. На рис. 2.8 приведена общая расчетная схема, пригодная для рассмотрения каждого из названных видов прямолинейных колебаний точки.

Вертикально подвешенная пружина имеет начальную длину (рис.2.8-а). При отсутствии нагрузки упругая сила пружины равна нулю.

При подвешивании тела весом она равна силе тяжести тела ( ) (рис. 2.8-б). Пружина растянута на величину статической деформации . Это положение тела удобно принимать за начало отсчета перемещений .