Лекция 14

Дифференциальные уравнения движения механической системы

в обобщенных координатах (уравнения Лагранжа II-го рода)

Уравнение Лагранжа II-го рода

Пусть имеется механическая система с голономными, идеальными, двусторонними связями с числом степеней свободы n. Это означает, что n обобщенных координат однозначно определяют положение системы и декартовы координаты любой МТ системы можно выразить через эти обобщенные координаты. Число МТ системы обозначим N. Связи системы считаем реономными, то есть в их уравнения явно входит параметр времени t. Тогда координаты к-той точки имеют вид

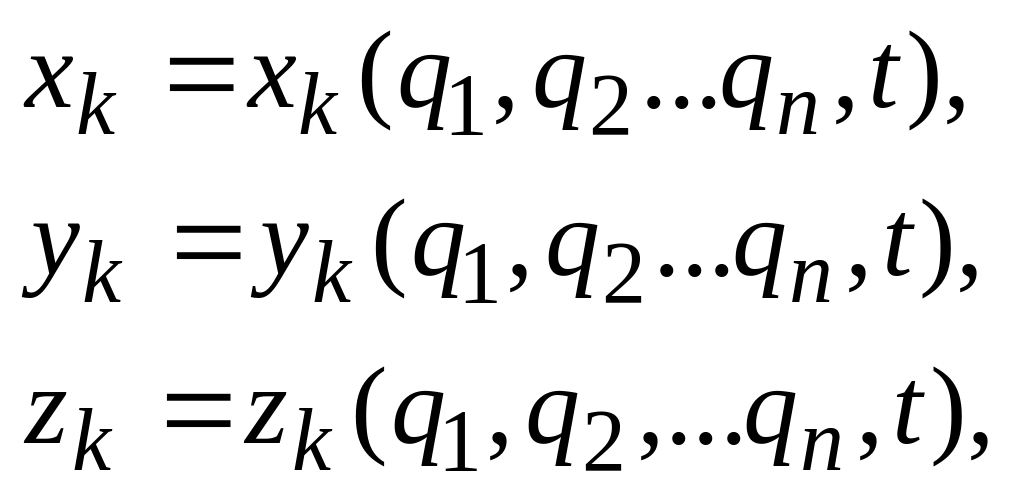(14.1)

и её радиус-вектор

. (14.2)

Применим общее уравнение динамики

. (14.3)

На основании (14.2) найдем возможное перемещение к-той точки через обобщенные координаты как полный дифференциал от вектора в рассматриваемый момент времени t

. (14.4)

В дальнейшем встретится двойное суммирование, поэтому заметим, что суммирование по индексу k производится по всем точкам системы от 1 до N, а по индексу i – по всем обобщенным координатам от 1 до n. Тогда соотношение (14.3) будет выглядеть

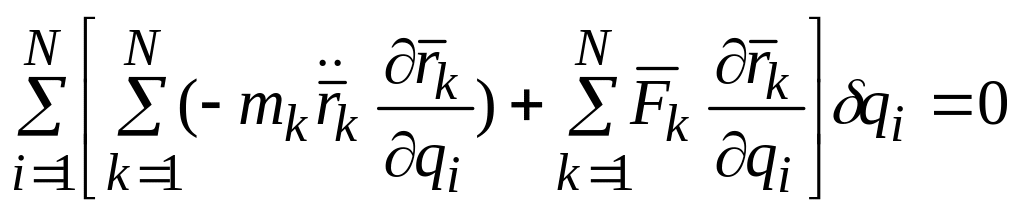. (14.5)

Заметим, что

,

откуда

. (14.6)

Установим необходимые для дальнейших рассуждений соотношения, которые возможны только для голономных механических систем. Сначала определим полную производную по времени радиуса-вектора на основании (14.2) (векторное выражение скорости к-той точки)

. (14.7)

Для обеих частей полученного равенства возьмем частные производные по обобщенным скоростям

. (14.8)

Выражение (14.8) является первым необходимым соотношением для получения второго искомого соотношения. Найдем частную производную от обеих частей равенства (14.7) по (от t зависят коэффициенты при обобщенных скоростях)

. (14.9)

Составим полную производную по времени от функции которая явно зависит от всех обобщенных координат и от времени t,

. (14.10)

Заметим, что правые части (14.9) и (14.10) одинаковы, следовательно

. (14.11)

Найдено второе необходимое соотношение.

Подставляем (14.8) и (14.11) в (14.6)

. (14.12)

Подставляем правую часть (14.12) под знак первой внутренней суммы соотношения (14.5)

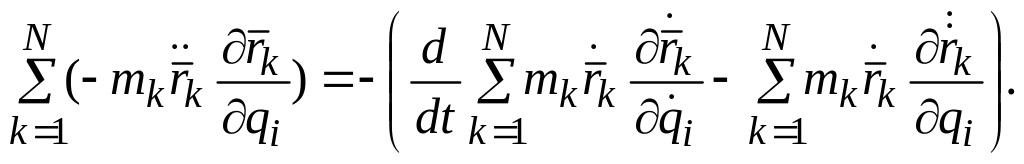(14.13)

Произведем преобразование правой части (14.13). Напишем выражение кинетической энергии системы

.

Заметим, что и что . Тогда

.

Из (14.7) видно, что функция зависит от всех и .

Составим частные производные от кинетической энергии Т по переменным и . Заметим, что

.

Тогда

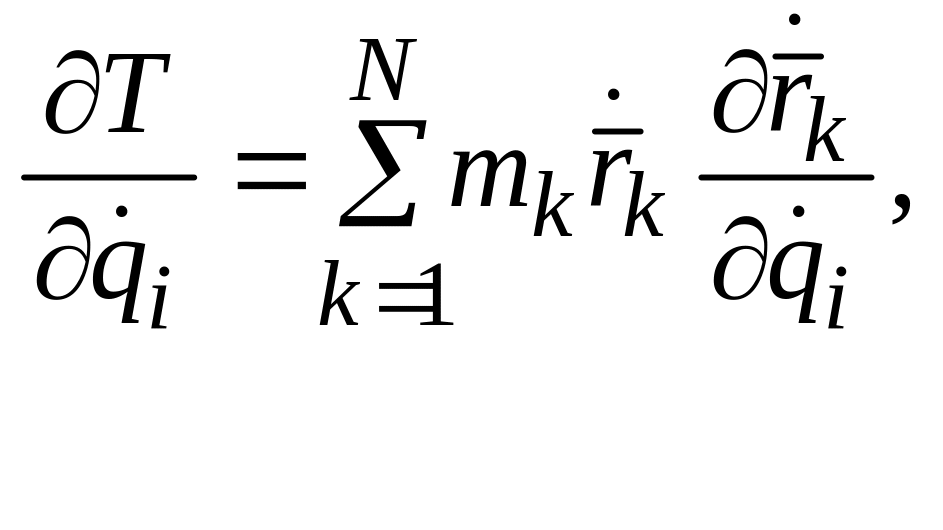(14.14)

(14.15)

Благодаря соотношениям (14.14) и (14.15) выражение (14.13) принимает вид

.

Вторая внутренняя сумма правой части (14.5) представляет собой обобщенную силу

.

Таким образом, уравнение (14.5) имеет вид

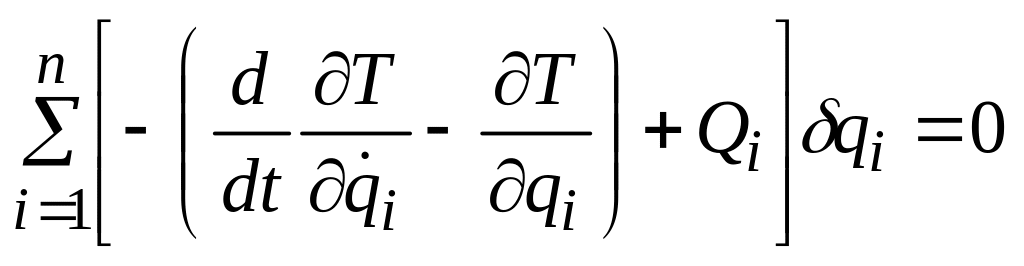. (14.16)

Уравнение (14.16) называется общим уравнением динамики в обобщенных координатах. В нем член

выражает сумму элементарных работ всех сил инерции в системе на возможном ее перемещении, соответствующем совокупности приращений обобщенных координат .

Уравнение (14.16) применимо для любой совокупности независимых величин в том числе и для случаев, когда одна из них не равна нулю, другие из них равны нулю (то есть изменяется только одна координата, а остальные постоянны).

Тогда можно, поочередно рассмотрев эти случаи, записать в общем виде (избавившись от знака суммы по n)

(i=1,2,3,…,n),

или окончательно

(i=1,2,3,…,n). (14.17)

Выражение (14.17) называется уравнением Лагранжа II-го рода.

Для механической системы их записывается столько, сколькими степенями свободы она обладает.

Пример.

М еханическая система состоит из ступенчатого барабана 1 и катка 2 (рис. 14.1-а) (их считать однородными цилиндрами). На участке нити КЕ, связывающей барабан с катком, имеется пружина с коэффициентом жесткости с. Система начинает двигаться из состояния покоя, при этом пружина не деформирована.

Дано: , , , , с.

Определить удлинение пружины в зависимости от времени , а также частоту и период колебаний.

Решение.

Система имеет две степени свободы, поэтому можно написать два уравнения Лагранжа II рода. За обобщенные координаты примем угол поворота диска 1 и перемещение центра колеса 5 (точки Е) (рис. 14.1-б).

Тогда

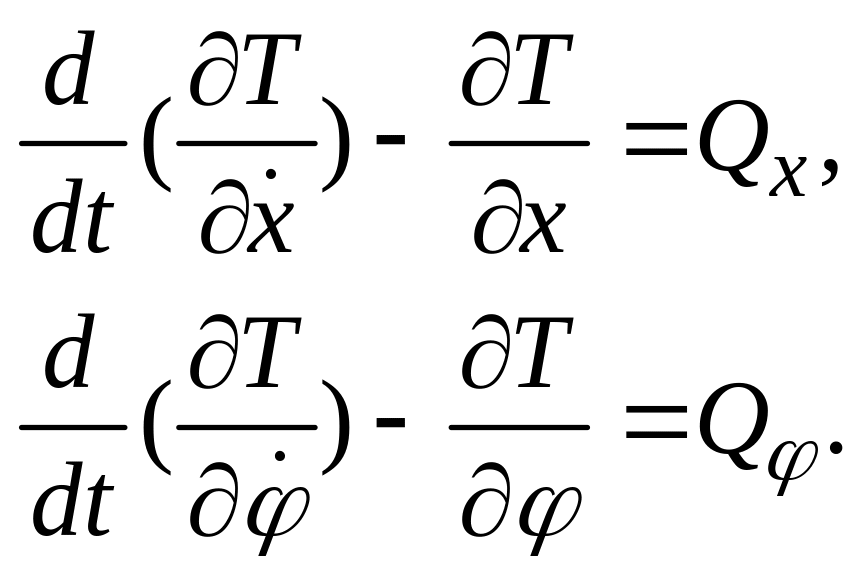(14.18)

Для определения кинетической энергии системы найдем скорости. Абсолютная скорость точки Е , угловая скорость катка 2

.

Определим кинетическую энергию тел.

Вращающийся вокруг неподвижной оси диск 1

.

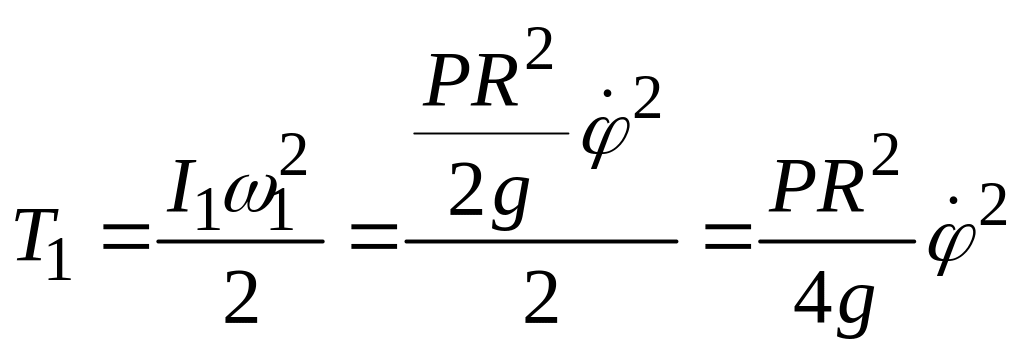Каток 2 находится в плоскопараллельном движении, поэтому

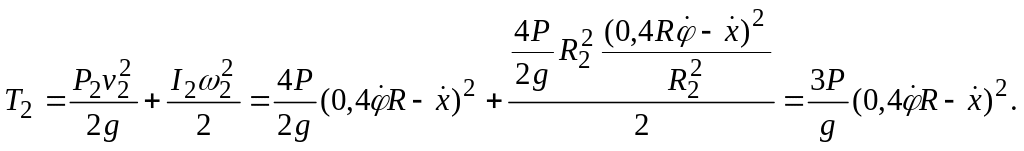
Общая кинетическая энергия системы

Производные

, ;

, ;

, .

Находим обобщенные силы. Каждая из них эквивалентна внешним силам по работе, производимой ими на перемещениях точек их приложения, вызванных приращением только соответствующей обобщенной координаты в предположении, что остальные обобщенные координаты приращений не имеют.

Поэтому

откуда

откуда .

Подставляем найденные выражения в исходную систему уравнений (14.18)

,

,

или

,

.

Отсюда

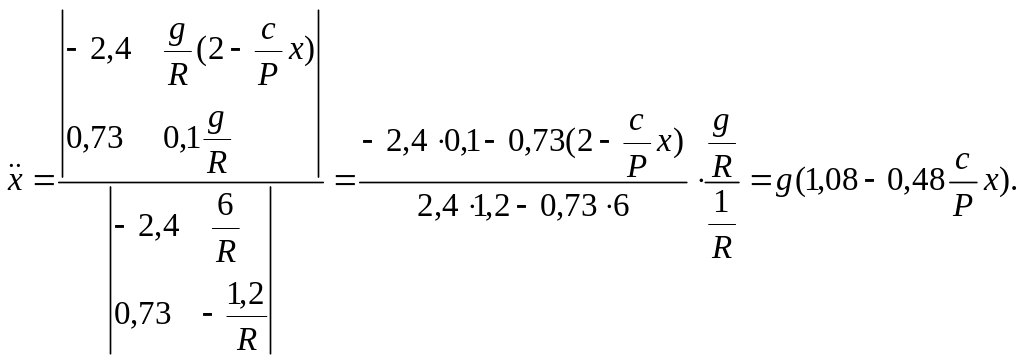
Следовательно,

, или ,

где .

Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, неоднородное. Его общее решение есть сумма общего решения однородного и частного решения неоднородного уравнений:

Общее решение однородного уравнения

.

Частное решение неоднородного уравнения находим их условия .

.

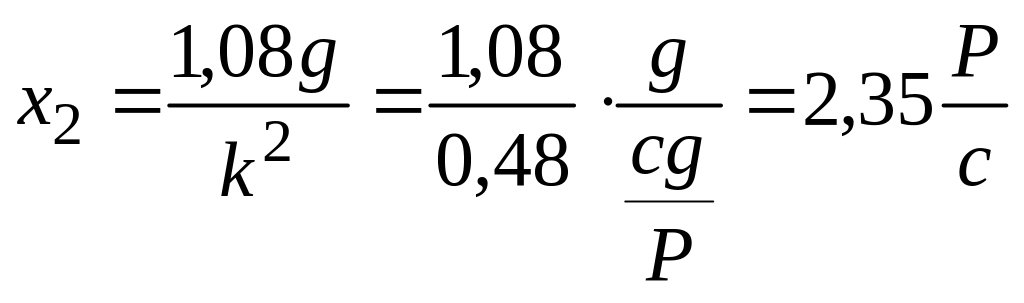Общее решение дифференциального уравнения

.

Из начальных условий находим постоянные А и В. При

, откуда ;

, откуда .

Тогда

.

Частота колебаний

,

период колебаний

.