Теорема Лагранжа-Дирихле

Пусть имеется механическая система с голономными стационарными связями, находящаяся под действием сил, имеющих потенциал (такая система называется консервативной). В положении ее равновесия каждая обобщённая сила равна нулю. Для случая потенциального силового поля обобщённые силы выражаются через потенциальную энергию по формулам

. (15.1)

Следовательно, в положении любого равновесия консервативной механической системы

, (15.2)

поэтому потенциальная энергия достигает своего экстремума.

По этим уравнениям ещё нельзя судить об устойчивом равновесии системы. Они определяются теоремой Лагранжа-Дирихле: для устойчивого положения равновесия консервативной механической системы достаточно, чтобы потенциальная энергия системы в этом положении имела минимум.

Для консервативной системы с одной степенью свободы условия равновесия определяется одним соотношением

. (15.3)

Для устойчивого равновесия необходимо выполнение условия минимума

>0. (15.4)

Если , то такая вторая производная не может служить критерием оценки устойчивости равновесия. В этом случае необходимо исследовать производные более высокого порядка .

Если первая не равная нулю производная имеет чётный порядок и при этом положительна, то при потенциальная энергия имеет минимум. Следовательно, это положение системы устойчиво.

Если же первая не равная нулю производная имеет нечётный порядок, то при нет ни минимума, ни максимума.

Критерий Лагранжа-Дирихле является достаточным, но не необходимым условием равновесия консервативной механической системы.

П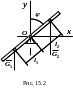 ример. Определить условия устойчивого равновесия механической системы с одной степенью свободы.

Требуется установить условия устойчивого равновесия метронома (рис. 15.2).

За обобщённую координату примем угол . Тогда потенциальная энергия имеет вид

.

При указанном на чертеже положении

,

следовательно,

.

Найдем первую и вторую производные от потенциальной энергии по обобщенной координате

,

.

В состоянии равновесия

.

Это возможно в двух случаях.

Случай 1. При , то есть при .

Случай 2. При , то есть при или .

При имеем , то есть нет ни минимума, ни максимума, что соответствует состоянию безразличного равновесия ( ).

При метроном находится в устойчивом равновесии, если

>0, то есть > .

При условие устойчивого равновесия можно получить, если

>0, то есть > .

В других случаях (при > , при > ) положение равновесия не устойчиво.

Малые колебания механической системы с одной степенью свободы

Механическая система может совершать колебания только вблизи устойчивого положения равновесия. Обобщенные координаты системы в положении равновесия принимаются равными нулю, то есть они отсчитываются из положения равновесия. Тогда колебательным движением механической системы в общем случае считают всякое её движение, при котором все обобщённые координаты или часть из них изменяются не монотонно, а имеют колебательный характер, то есть принимают нулевые значения, по крайней мере, несколько раз.

Для механической системы с одной степенью свободы уравнение Лагранжа II рода можно написать только одно. В общем случае оно имеет вид

,

где обобщенную силу Q можно считать состоящей из трёх частей

. (15.5)

Здесь - обобщённая сила потенциальных сил. Она зависит от обобщенной координаты и не зависит от обобщенной скорости . В случае нестационарного силового поля она может зависеть от времени (собственные колебания).

- часть обобщенной силы, зависящая от сил сопротивления, являющихся функцией величин и направлений скоростей. В нашем курсе ограничиваемся случаем линейного сопротивления (в затухающих колебаниях ).

В общем случае силу можно разложить в ряд Фурье и рассматривать каждое из синусоидальных слагаемых в отдельности, а результат получить методом наложения решений по принципу независимости действия сил.