3.7. Особый случай

До сих пор мы рассматривали ситуацию, когда один договор мог породить не более одного страхового случая. При обоснованном требовании страховщик выплачивал возмещение, т.е. выполнял свои обязательства, и на этом действие договора прекращалось, хотя стороны могли составить новый договор.

Однако возможна ситуация, когда, согласно договору, например, в автотранспортном страховании, страховщик несет ответственность в течение определенного времени, даже, если возникнет несколько страховых случаев, т.е. когда один договор может породить несколько исков.

Если ущерб в i-м случае равен Y_i, то общий ущерб составит: X=ΣY_i, i=1, …, k. Предполагается, что Y_i – независимы, хотя, в действительности это условие не всегда выполняется; например, автомобиль после ремонта имеет больше шансов попасть в аварию, чем новый. Следует также учитывать, что на частоту наступления страховых случаев могут влиять одни факторы (например, возраст водителя), а на величину предъявляемого иска – другие (марка автомобиля). Поэтому предварительно весь портфель разбивается на несколько однородных субпортфелей. Вначале предположим, что портфель однороден, и проанализируем X.

;

;

.

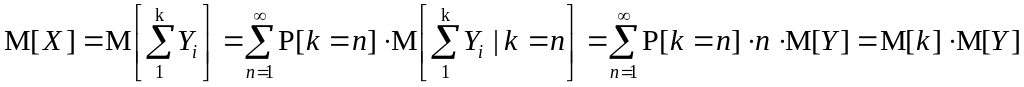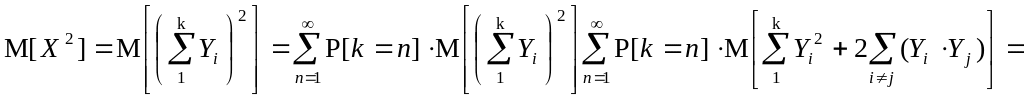
Итак, получены выражения для М(Х), D(X). Это позволяет оценить степень риска.

3.8. Использование отрицательного биномиального распределения при моделировании потока требований об оплате

Это распределение числа страховых случаев используется аналогично распределению Пуассона, однако, имеет особенности.

Например, при страховании автомобиля от аварии интенсивность зависит от числа дней с плохой погодой. Т.е. не является константой, а представляет из себя случайную величину с некоторой плотностью распределения f_λ. Поэтому возникает необходимость предварительного усреднения параметра λ, используя это распределение.

.

Если N договоров разбиты на k однородных групп (по возрасту водителя, особенностями его здоровья и характера, сложности маршрутов его поездок и т.д.) с N_i договоров в каждой группе, то в каждой группе можно использовать пуассоновскую модель со своим постоянным значением параметра λ_i. Доля этой группы в общем портфеле N_i/N=A_i.

Рассмотрим наудачу выбранный договор (не зная, к какой группе он принадлежит). Случайное событие B_i состоит в принадлежности выбранного довора к i-й группе. Для этого договора распределение числа исков за рассматриваемый период равно:

;

где среднее берется по распределению A_i (при увеличении числа договоров используется непрерывная аппроксимация).

Итак, параметр λ подчиняется Гамма-распределению Γ(β, α)

.

Это - удобная модель, если λ колеблется около λ₀ с возможными, но маловероятными большими отклонениями. Тогда:

;

t =(β+1)x;

.

Учитывая, что Γ(х)=(х-1)·Γ(х-1), получим окончательно:

П_i =(1/i!)·α(α+l)…(α+I–l)·p^α–q^j, где р=β/(β+l), q=1/(β+1).

Если вероятности обладают указанным свойством, то распределение называется отрицательным биномиальным с параметрами: р и α.

Соответствующая производящая функция:

;

M(k)=П'(1)=αq/p, D(k)=П''(1)+П'(1)–(П'(1))²=αq/p²; т.е. D(k)=M(k)/p>M(k).

Пример 37. Портфель составляет 50000 договоров автотранспортного страхования. Согласно собранной статистике о числе аварий за год: m₀=40544, m₁=8082, m₂=1205, m₃=145, m₄=20, m₅=3, m₆=1. Требуется смоделировать число аварий.

Найдем среднее значение и дисперсию числа аварий на один договор. М=0.22056, D=0.2441182 (т.е. на 10% больше). Для распределения Пуассона эти величины должны совпадать (при столь большом N), поэтому различие в 10% вызывает сомнение в возможности использовать пуассоновскую модель. Однако достоинства последней заставляют "попытать счастья".

Составим таблицу:

i	mi	mi(т)
0	40544	40103
1	8082	8845
2	1205	975
3	145	72
4	20	4
5	3	0
6	1	0

Видно, что пуассоновская модель неадекватна, причем отклонения подталкивают страховщика к неоправданному оптимизму, а это вызовет жестокое разочарование на практике. Следовательно, наши надежды на пуассоновскую модель не оправдались, поэтому мы вынуждены усложнить модель и использовать отрицательное биномиальное распределение.

Из свойств этого распределения известно: M(k)=αq/p, D(k)=αq/p²;. Получили систему уравнений для p и α, решая которую: p=M/D=0.93, и α=М²/(D–М)=2.06, получили значения параметров для модели.

Используя последние, найдем теоретические частоты, соответственно:

40547 8080 1195 156 19 2 0.

Расхождение с эмпирическими частотами минимально, модель адекватна.