5.5.Некоторые элементы теории фотоэлектронной эмиссии

В последние годы была разработана более строгая теория фотоэмиссии, учитывающая кристаллическую структуру твердых тел и взаимодействие электронов с решеткой. Как отмечалось выше (раздел 5.2), в настоящее время преимущественно рассматривается трехступенчатая модель: возбуждение электрона за счет поглощения фотона – движение фотоэлектрона к поверхности – преодоление барьера на поверхности.

О

Рис.5.5.1. Одноступенчатая модель фотоэмиссии.

днако в ряде случаев более предпочтительной оказывается одноступенчатая модель (рис.5.5.1). В этом случае при возбуждении электрон переходит в состояние, которое является разрешенным в вакууме, но затухает при удалении от поверхности. Все же это сравнительно редко встречающийся случай. В большинстве случаев фотоэлектронные спектры анализируются с позиций трехступенчатой модели, основные моменты которой рассмотрим ниже.

5.5.1. Возбуждение фотоэлектрона

На первом этапе фотоэмиссии происходит поглощение кванта света, приводящее к возбуждению электрона из начального состояния с энергией E_i в конечное с энергией E_f. Процесс сложен и может быть рассмотрен только в рамках квантовой механики при решении нестационарного уравнения Шредингера. Схема такого решения следующая. Пусть имеем систему, для которой в случае отсутствия возмущения справедливо следующее волновое уравнение:

(5.5.1)

где - гамильтониан невозмущенной системы. Решение уравнения известно:

(5.5.2)

где _n(r) – функция только от координаты, а E_n – собственные значения энергии.

Допустим, что на систему, начиная с некоторого момента t=0, оказывает воздействие слабое возмущение W(t). Тогда, решив волновое уравнение:

(5.5.3)

можно найти значение  в любой последующий момент времени. Если возмущение не велико, то можно искать решение в виде линейной комбинации волновых функций, соответствующих невозмущенной системе:

(5.5.4)

где a_n(t) – коэффициенты разложения, которые необходимо определить. Физический смысл этих коэффициентов очевиден: |a_n(t)|² - вероятность того, что в момент t система находится в состоянии n. При этом если в начальный момент времени она находилась в основном состоянии , то |a₀(t)|² равно единице при t=0 и убывает в дальнейшем, а остальные a_n изменяются по некоторому закону, зависящему от характера возмущения.

Подставляя в (5.5.3) волновую функцию в виде суммы (5.5.4), получаем:

(5.5.5)

Поскольку есть решение в случае отсутствия возмущения, то в правой и левой частях есть равные величины. После их сокращения получаем:

(5.5.6)

Будем считать, что вследствие малости возмущения изменение волновой функции не велико и можно заменить (r,t) ее невозмущенным значением . Умножая обе части уравнения на и интегрируя по всему пространству, имеем:

(5.5.7)

В результате интегрирования уравнения получаем:

(5.5.8)

При освещении возмущением является поле световой волны. Электромагнитное поле, имеющее напряженность электрического поля и напряженность магнитного поля , может быть описано с помощью скалярного потенциала 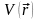и векторного потенциала , так что:

(5.5.9)

В частности, для линейно поляризованного света величину векторного потенциала можно представить в виде:

(5.5.10)

где  - частота света, - волновой вектор фотона. Соответствующий этому случаю оператор Гамильтона записывается следующим образом:

(5.5.11)

где U – потенциальная энергия системы.

Преобразуем гамильтониан, для чего рассмотрим составляющую по координате х:

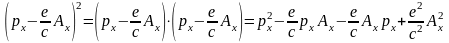(5.5.12)

Используя перестановочные соотношения Гейзенберга:

(5.5.13)

получаем:

(5.5.14)

Аналогичные выражения справедливы и для других составляющих векторов-операторов.

В результате гамильтониан имеет следующий вид:

(5.5.15)

Для световой волны вектор-потенциал и скалярный потенциал всегда можно выбрать так, что 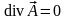и V=0. Тогда, пренебрегая величиной члена с , как величиной второго порядка малости, можно записать гамильтониан в виде:

(5.5.16)

так что в первом приближении возмущение, вызываемое световым полем, описывается последним слагаемым:

(5.5.17)

Для удобства в дальнейшем запишем величину, стоящую перед градиентом в следующем виде:

(5.5.18)

где G – комплексная функция, а G⁺ - эрмитово сопряженная величина. Подставляя выражение в (5.5.8) получаем:

(5.5.19)

Интегрируя по времени, имеем:

(5.5.20)

Т.к. E_f – E₀ > 0 и h имеет большое значение, то можно ограничиться только первым слагаемым. Действительно, уже при незначительных отклонениях энергии кванта света h от разности энергии перехода из начального состояния электрона 0 в конечное состояние f, т.е. E_f –E₀ , вероятность перехода становится пренебрежимо малой величиной. Пусть, например, E_f – E₀ - h =10 ^-5эВ, что соответствует при h =3эВ (=4120 Å) отличию в величине длины волны всего лишь на 0,014 Å (энергия фотона 3,00001эВ соответствует =4119,986 Å). Тогда:

(5.5.21)

Модуль числителя в слагаемых (5.5.20) не превышает 2, поэтому вполне можно пренебречь вторым слагаемым, в знаменателе которого стоит сумма разности энергий состояний электрона и энергия фотона. Таким образом, получаем:

(5.5.22)

Вероятность перехода есть квадрат модуля коэффициента:

(5.5.23)

Полученное выражение может быть записано в несколько иной форме, если учесть, что [4, с.181]:

(5.5.24)

В итоге получаем:

, (5.5.25)

где использовано соотношение: (ax)=(x)/a. Такая запись по существу означает, что должен выполняться закон сохранения энергии.

Если имеется не одно, а несколько конечных состояний, имеющих одинаковую энергию E_f, то полная вероятность будет равна сумме вероятностей перехода в каждое из них, т.е.:

, (5.5.26)

Соответственно, вероятность перехода в единицу времени можно записать в виде:

(5.5.27)

Это выражение называют «золотым правилом» Ферми.

В большинстве интересных для нас случаев поглощение кванта света приводит к переходу в континуум состояний. Поэтому полезно ввести плотность состояний (E), которая характеризует число энергетических состояний, приходящееся на единичный интервал энергии. Тогда суммирование в (5.5.27) нужно заменить интегрированием и, учитывая, что число состояний, приходящихся на энергетический интервал dE равно (E)dE, имеем:

(5.5.28)

Вероятность возбуждения электрона фотоном из состояния, имеющего энергию Е₀, таким образом, определяется плотностью конечных состояний и величиной матричного элемента:

(5.5.29)

г

Рис.5.5.2. Дисперсионная зависимость в случае свободных электронов. Нет разрешенных для электронов состояний, в которые мог бы перейти электрон при поглощении кванта света.

де интегрирование ведется по всему пространству.

В случае свободных электронов матричный элемент перехода отличен от нуля только в том случае, если выполняется соотношение:

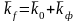, (5.5.30)

которое представляет собой запись сохранения количества движения. Действительно, в этой модели волновая функция представляет собой плоскую волну:

(5.5.31)

Используя (5.5.28) и (5.5.29) получаем:

(5.5.32)

Интеграл в этом выражении отличен от нуля только в случае, если выполняется соотношение (5.5.30), т.е. выполняется закон сохранения импульса. На рис.5.5.2 приведена дисперсионная зависимость E(k). Величина k_ф мала. Например, при =1000 Å имеем:

. (5.5.33)

Чтобы убедиться, насколько мала эта величина, рассчитаем, чему равна величина k у электронов, находящихся на уровне Ферми в случае серебра. Используя величину энергии Ферми, полученную ранее (1.1.31), имеем:

(5.5.34)

Видно, что волновые числа электронов на много порядков превышают волновые числа фотонов. Поэтому на дисперсионной зависимости поглощение фотона изображается практически вертикальной линией. Но в случае свободных электронов им некуда переходить– отсутствуют разрешенные состояния. Свободные электроны не способны поглощать кванты света. Поэтому их фотовозбуждение возможно только в том случае, если в процессе участвует третье тело, только в этом случае могут быть выполнены оба закона сохранения. Естественно предположить, что в качестве такового выступает решетка, в поле ионов которой происходит движение электронов.

Поведение электронов, движущихся в периодическом поле кристаллической решетки, может быть описано волновыми функциями Блоха. Для простоты рассмотрим одномерный случай - цепочку атомов длиной L = aN, где а – постоянная решетки. Тогда:

( 5.5.34)

где u(x) – периодическая функция с периодом, равным постоянной решетки:

(5.5.35)

Подставим волновые функции в таком виде в выражение для матрицы перехода (5.5.28):

(5.5.36)

Разобьем весь интервал интегрирования на N частей от 0 до а, от а до 2а и т.д. Рассмотрим отдельно интеграл по отрезку от па до (п+1)а. Воспользовавшись периодичностью функции и(х) и делая замену переменной x’=x-an получаем:

(5.5.37)

Это позволяет свести интеграл (5.5.36) к сумме:

(5.5.38)

т.ч. величина R_f0 определяется суммой геометрической прогрессии:

Рис.5.5.3. Расширенная зона Бриллюэна.

(5.5.39)

Легко убедиться, что она имеет ненулевое значение только в случае, если показатель экспоненты равен вектору обратной решетки , который равен целому числу, умноженному на 2/а, т.е.

(5.5.40)

Действительно, если это условие выполняется, то экспонента под знаком суммирования равна 1, и S_N =N. Если же разность , то, используя правило суммирования геометрической прогрессии, имеем:

(5.5.41)

Величиной k_ф можно пренебречь, ввиду малости волнового вектора фотона, поэтому скобка в числителе оказывается равной нулю, поскольку и k_f , и k₀ есть целое число, умноженное на 2/а.

Таким образом, учет взаимодействия с решеткой показывает, что поглощение кванта света электроном возможно, если разность импульсов в начальном и конечном состояниях отличается на величину вектора обратной решетки. На рис.5.5.3 приведена расширенная зонная схема. Требование (5.5.40) выполняется для перехода, обозначенного штриховой линией. На приведенной зонной схеме этому соответствует вертикальный переход. Такие переходы называют прямыми. Важно отметить, что речь идет о переходах между зонами Бриллюена, а не энергетическими зонами. Если энергетическая зона сложная, имеющая несколько различных ветвей E(k), то возможны переходы в пределах одной энергетической зоны.

Э

Рис.5.5.4. Наряду с прямыми переходами, возможны непрямые при участии фононов.

то самый простой вариант, но не единственный, что с очевидностью следует из факта совпадения фотоэлектрической и термодинамической работ выхода металлов. При фотовозбуждении приведенное волновое число может быть изменено за счет получения или потери импульса от фононов или дефектов, или поверхности. Последнюю можно рассматривать как большой дефект. Переходы, при которых изменяется волновое число, называют непрямыми.

В

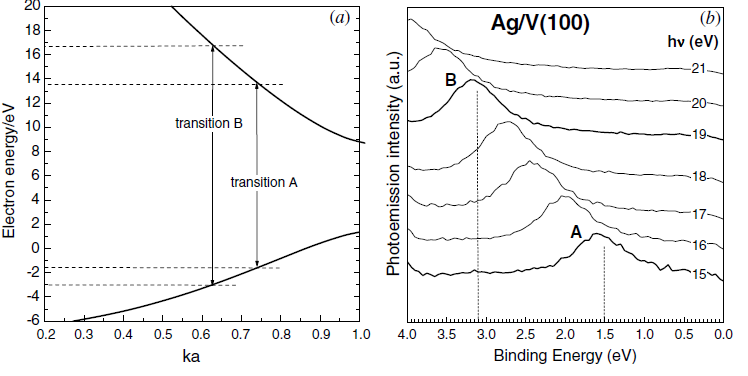
Рис.5.5.5. Участок дисперсионной кривой и соответствующие фотоэлектронные спектры, полученные при различных энергиях фотонов. Спектры смещены на произвольные величины вдоль оси ординат.

случае прямых переходов фотоэлектронная работа выхода оказывается зависящей от энергии кванта света. Она увеличивается с ростом h. Причина этого понятна, если обратиться к дисперсионным кривым E(k) (рис.5.5.4). Действительно, предположим, что фотоэлектроны возникают только в результате прямых переходов. Тогда видно, что выйти в вакуум способны те электроны, которые располагаются на уровнях ниже верха валентной зоны. При увеличении h оптически могут возбуждаться только электроны с еще более глубоких состояний. Это и приводит к зависимости _ф от h, характер которой определяется дисперсионными кривыми.

Непрямые переходы играют второстепенную роль. Они, наряду с рассеянными фотоэлектронами, создают диффузный фон, на пъедестале которого выделяются пики, вызванные прямыми межзонными переходами.

а	б
Рис.5.5.6. Схематическое представление фотоэмиссионных спектров при различных энергиях фотонов (б). а – приведенная зона Бриллюэна, отмечены возможные прямые переходы.

На рис.5.5.6 схематически приведены фотоэлектронные спектры, которые могут быть получены при использовании фотонов с разной энергией. На шкале абсцисс отложена энергия связи, т.е. энергия состояний, из которых имеет место возбуждение фотоэлектронов. Соответствующие гипотетические дисперсионные зависимости приведены на том же рисунке. При энергии кванта света h₁ возможен прямой переход, что приводит к появлению максимума на фотоэлектронном спектре при энергии Е₁. При увеличении энергии фотона (h₂) по-прежнему возможен прямой переход, однако начальное состояние находится при более низкой энергии. Поэтому пик на фотоэлектронном спектре хотя и смещается в сторону более высоких кинетических энергий, но на меньшую величину, чем изменяется энергия фотона. В случае h₃ отсутствует возможность прямых переходов. На спектре отсутствуют ярко выраженные особенности. Они появляются вновь при энергиях h₄, когда становится возможным прямой переход в следующую зону. При дальнейшем увеличении кванта (h₅) пик смещается в сторону больших энергий, поскольку повышается энергия начальных состояний. Таким образом, из изменения фотоэлектронных спектров при изменении энергии фотонов можно получить информацию об энергетической структуре зоны Бриллюэна.