4.6. Графический метод решения игр и .

Поясним метод на примерах.

Пример 1. Рассмотрим игру, заданную платёжной матрицей.

На плоскости хОу введём систему координат и на оси Ох отложим отрезок единичной длины A₁, А₂, каждой точке которого поставим в соответствие некоторую смешанную страте­гию игрока 1 (х, 1 - х). В частности, точке A₁ (0;0) отвечает стратегия A₁, точке А₂ (1;0) - стра­тегия А₂ и т.д.

В точках A₁ и А₂ восстановим перпендикуляр и на полученных прямых будем отклады­вать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью Оу) отложим выигрыш игрока 1 при стратегии A₁, а на втором - при стратегии A₂. Если игрок 1 применит стратегию A₁, то выиграет при стратегии B₁ игрока 2-2, при стратегии В₂ - 3, а при стратегии В₃ - 11. Числам 2, 3, 11 на оси Ox соответствуют точки B₁, B₂, B₃

Если же игрок 1 применит стратегию А₂, то его выигрыш при стратегии B₁ равен 7, при В₂ - 5, а при В₃ - 2. Эти числа определяют точки B’₁, B’₂, B’₃ на перпендикуляре, восстановлен­ном в точке А₂. Соединяя между собой точки B₁ и B’₁, B₂ и B’₂, B₃ и B’₃ и получим три прямые, расстояние до которых от оси Ох определяет средний выигрыш при любом сочетании соответ­ствующих стратегий. Например, расстояние от любой точки отрезка B₁B’₁ до оси 0х определяет средний выигрыш υ₁ при любом сочетании стратегий A₁A₂ (с частотами х и 1-х) и стратеги­ей В₁ игрока 2. Это расстояние равно

2х₁ +6 (1 – х₂) = υ₁

(Вспомните планиметрию и рассмотрите трапецию А₁В₁В`₁А₂). Таким образом, ординаты то­чек, принадлежащих ломанной В₁ М N B’₃ определяют минимальный выигрыш игрока 1 при применении им любых смешанных стратегий. Эта минимальная величина является максималь­ной в точке N; следовательно этой точке соответствует оптимальная стратегия X* = (х, 1-х), а её ордината равна цене игры υ. Координаты точки N находим как точку пересечения прямых B₂B’₂ и B₃B’₃

Соответствующие два уравнения имеют вид

 .

Следовательно , при цене игры . Таким образом, мы можем найти оптимальную стратегию при помощи матрицы

Оптимальные стратегии для игрока 2 можно найти из системы  и, следовательно, ). (Из рисунка видно, что стратегия B₁ не войдёт в оптималь­ную стратегию).

Пример 2. Найти решение игры, заданной матрицей

Решение. Матрица имеет размерность 2х4. Строим прямые, соответствующие стратеги­ям игрока 1.

Ломанная A₁ К А'₄ соответствует верхней границе выигрыша игрока 1, а отрезок N К - цене игры. Решение игры таково

4.7. Сведение матричной игры к задаче линейного программирования.

Предположим, что цена игры положительна (v > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и, следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменя­ются.

Итак, пусть дана матричная игра с матрицей А порядка т х п. Согласно свойству 7 опти­мальные смешанные стратегии х = (x₁, ..., х_m), у = (y₁, ..., у_n) соответственно игроков 1 и 2 и це­на игры и должны удовлетворять соотношениям.

(1)

(2)

Разделим все уравнения и неравенства в (1) и (2) на  (это можно сделать, т.к. по предположе­нию v > 0) и введём обозначения:

Тогда (1) и (2) перепишется в виде:

Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i, чтобы цена игры  была максимальной, то решение первой задачи сводится к нахождению таких неотри­цательных значений р_i (i = ), при которых

Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена иг­ры v была наименьшей, то решение второй задачи сводится к нахождению таких неотрица­тельных значений q_j (j = ), при которых

(4)

Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).

Решив эти задачи, получим значения р_i (i = ), q_j (j = ) и . Тогда смешанные стратегии, т.е. х_i и у_j получаются по формулам :

х=vp_i (i = ), y = vq_j (j = )

Для того чтобы число v было ценой игры, а , были оптимальными стратегиями игроков А и В, необходимо и достаточно выполнение неравенства:

(гарантированный выигрыш)

(гарантированный проигрыш)

Игрок А имеет «m»-стратегий, а игрок В – «n»-стратегий.

Для 1-го игрока: . Получаем задачу линейного программирования для игрока А. .

Для 2-го игрока: Получаем задачу линейного программирования для игрока B. .

Эти две задачи являются двойственными задачами линейного программирования. Решая одну из них, получаем решение и другой задачи. За основу лучше брать задачу для игрока В (решение симплекс-методом). При составлении симплекс-таблицы следует помнить, что базисным переменным 2-ой задачи соответствуют свободные переменные 1-ой задачи, а базисным переменным 1-ой задачи – наоборот.

Пример 1.

Молочный комбинат «Ставропольский» планирует выпуск двух видов новой продукции: питьевой биойогурт и пудинг сливочный. Спрос на эти продукты не определен, но можно предположить, что он принимает одно из двух состояний: хороший и удовлетворительный. В зависимости от этих состояний прибыль комбината различна и определяется матрицей К: .

Найти оптимальное соотношение между объемами выпуска каждого из продуктов, при котором комбинату гарантирована средняя прибыль при любом состоянии спроса.

Решение.

Минимизируем элементы строк матрицы

α1= min (3,5)=3

α2= min (4,2)=2

Найдем нижнюю цену игры

α= maxmin (3,2)=3

Максимизируем элементов столбцов матрицы

β1=max(3,4)=4

β2=max(5,2)=5

Найдем верхнюю цену игры

α =minmax(4,5)=4

Т. К. нижняя и верхняя цены игры не равны, то игра производится в смешанных стратегиях, седловой точки нет.

Решим игру в смешанных стратегиях. Пусть х – вероятность применения 1 стратегии 1 игроком, (1-х) – вероятность применения 2 стратегии 1 игроком. Тогда

V = 3x + 4 - 4x = 4 – x - уравнение прямой L1

V = 5x + 2 - 2x = 3x + 2 - уравнение прямой L2

Строим систему координат х0у и на оси 0х отложим отрезок единичной длины (т.к. мы находим вероятность применения каждым из игроков своих смешанных стратегии, а вероятность находится от 0 до 1).

Строим прямые L1 и L2. Из точки пересечения прямых опускаем перпендикуляр на ось 0х и находим х.

4 - х = 3х + 2

4х = 2

х = ½ - вероятность применения 1 стратегии

1 – х = 1 – ½ = ½ - вероятность применения 2 стратегии.

Х( ½ , ½ )

Найдем цену игры

V = 4 – ½ = 3 ½

Пусть у – вероятность применения 1 стратегии 2 игроком, (1-у) – вероятность применения 2 стратегии 2 игроком.

Аналогично находим:

У = ¾

1 – у = 1 – ¾ = ¼

У( ¾ , ¼ )

Найдем цену игры:

V = 2 ¾ + 2 =3 ½

Также данную задачу можно решить путем сведения ее к задаче линейного программирования.

Составим пару взаимно – двойственных задач.

Для 1 игрока:

3t₁ + 4t₂ ≥1

5t₁ + 2t₂ ≥1

Z ₁ = t₁ + t₂ min

Для 2 игрока:

3h₁ + 5h₂ ≤ 1

4h₁ + 2h₂ ≤ 1

Z₂ = h₁ + h₂ max

Приведем системы к каноническому виду.

3 t₁ + 4t₂ - t₃ = 1

5t₁ + 2t₂ – t₄ = 1

t ₃ = - 1 – (-3t₁ – 4t₂)

t₄ = - 1 – (-5t₁ – 2t₂)

Z ₁ = 0 – (-t₁ – t₂) min

3 h₁+ 5h₂ – h₃= 1

4h₁+ 2h₂– h₄ = 1

h ₃ = 1 – (3h₁ + 5h₂)

h₄= 1 – (4h₁ + 3h₂)

Z ₂= 0 – (-h₁– h₂) max

Решим задачу симплекс - методом.

Симплекс таблица № 1

	Bi	h1	h2
h3	1	3	5
h4	1	4	2
Z2	0	-1	-1

Т.к. строка Z₂ имеет отрицательные элементы, то строим симплекс-таблицу №2.

Симплекс таблица № 2

	Bi	h1	h3
h2	1/5	-3/4	1/5
h4	3/5	14/5	-2/5
Z2	1/5	-2/5	1/5

Т.к. строка Z₂ имеет отрицательные элементы, то строим симплекс

таблицу №3.

Симплекс таблица № 3

	Bi	h4	h3
h2	1/14	-3/14	2/7
h1	3/14	5/14	-1/7
Z2	2/7	1/7	1/7

Из таблицы находим:

t₁ = 1/7

t₂ = 1/7

Zmin = 2/7

h₁ = 3/14

h₂ = 1/14

Zmax = 2/7

Получаем:

V = 1/Z = 7/2 = 3 ½

Отсюда:

X₁ = vt₁ = 7/2* 1/7 = ½

X₂= vt₂ = 7/2 * 1/7 = ½

Y₁ = vh₁ = 7/2 * 3/14 =3/4

Y₂= vh₂= 7/2 * 1/14 = ¼

Ответ: для комбината гарантирована средняя прибыль 3 ½ при производстве 50% от всего товара продукта А и при производстве 50% продукта В.
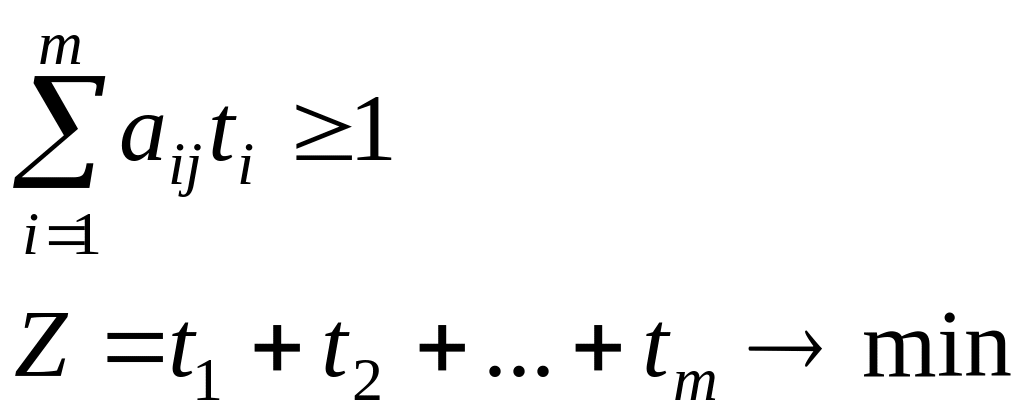