
- •Гармонический анализ
- •§1. Периодические функции.
- •Смотрите в лекции
- •§2. Гармонические колебания. Смотрите в лекции
- •§ 3. Тригонометрические ряды. Ряды Фурье. Основные понятия. Разложение в ряд Фурье функций с периодом 2.
- •Ряд Фурье в виде простых гармоник. Спектры.
- •§ 4. Разложение в ряд Фурье четных и нечетных функций периода 2.
- •Решение:
- •§ 5. Сдвиг основного промежутка.
- •Решение:
- •§ 6. Разложение в ряд Фурье функций с периодом 2ℓ.
- •Решение:
- •Решение:
- •§ 7. Разложение в ряд Фурье функций, заданных на полупериоде.
- •Решение:
- •§ 8. Разложение в ряд Фурье функций с “двойной симметрией”.
Решение:
График функции изобразим на рис. 5. Видно, что функция – разрывная. Найдем коэффициенты Фурье. Здесь
а0
=
![]()
![]() =
=
![]() ,
,
аn
=
![]() ,
(n=1,2,...),
,
(n=1,2,...),
bn
=
![]() .
.
Стало быть, при 0 < x < 2π будет
x =
![]() .
.
В точках x = 0 и x = 2 сумма S(x) ряда равна .
§ 6. Разложение в ряд Фурье функций с периодом 2ℓ.
Пусть функция f(x)
задана и дифференцируема на отрезке
[–l; l].
Положим φ(z) =
![]() .
.
Тогда φ(z) будет заданной и дифференцируемой уже на отрезке [–π; π].Значит к φ(z) применима теория, изложенная выше, поэтому при – π < z < π будет
φ(x)
=
+
![]() .
.
Положим в этом равенстве
![]() .
Тогда для – l < x
< l , то есть для
функций с любым периодом 2ℓ разложение
в ряд Фурье, когда оно возможно, и формулы
для коэффициентов Фурье таковы:
.
Тогда для – l < x
< l , то есть для
функций с любым периодом 2ℓ разложение
в ряд Фурье, когда оно возможно, и формулы
для коэффициентов Фурье таковы:
f(x)
=
![]() +
+![]()
![]() cos
cos![]() +
+
![]() sin
), (
1.25 )
sin
), (
1.25 )
где а0
=
![]() (x)dx;
аn=
(x)dx;
аn=
![]() x)
cos
dx;
bn=
x)
sin
dx
(1.26)
x)
cos
dx;
bn=
x)
sin
dx
(1.26)
Если f(x) – четная, то
![]() , (1.27)
, (1.27)
где а0
=
![]() (x)dx;
аn=
(x)
cos
dx
. (1.28)
(x)dx;
аn=
(x)
cos
dx
. (1.28)
Если f(x) – нечетная, то
![]() , (1.29)
, (1.29)
где
bn=
![]() (x)
sin
dx.
(1.30)
(x)
sin
dx.
(1.30)
Замечание. Можно от периода 2![]() перейти к периоду 2,
произведя замену переменной по формуле
х =
перейти к периоду 2,
произведя замену переменной по формуле
х =
![]() или х/ =
(x–l)
и затем вычислять коэффициенты Фурье
для 2
- периодических функций.
или х/ =
(x–l)
и затем вычислять коэффициенты Фурье
для 2
- периодических функций.
Пример 5.
Разложить в ряд Фурье функцию f(x) = x, заданную на интервале –2 х 2.
Решение:
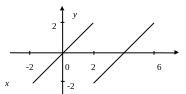
Рис. 6
График функции f(x) = x изображен на рисунке 6. Видно, что функция нечетная с периодом 2ℓ = 4, то есть ℓ = 2. Найдем коэффициенты Фурье по формуле 1.30.
bn
=
![]() dx =
dx =
![]() = –
= –![]() х
cos
х
cos![]() dx
=
dx
=
= –![]() cos
n
+
cos
n
+
![]() = –
cos
n
+
= –
cos
n
+
![]() sin n
= –
cos
n
=
sin n
= –
cos
n
=
=
![]()
Следовательно, по 1.29 разложение в ряд Фурье функции f(x) имеет вид:
f(x)
= x =
![]() –
–
![]() +
+
![]() –
... = –
–
... = –
![]() .
.
Пример 6.
Р
f(x)
=
![]()
Решение:
Воспользуемся замечанием. Произведем
замену переменой х =
![]() ,
т.о. получаем функцию:
,
т.о. получаем функцию:
f
при 0 <
х
/
<
.
при -
<
х
/
0,![]()
Найдем коэффициенты Фурье.
а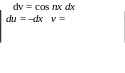 0
=
0
=
![]() dx
/
+
dx
/
+
![]() dx
/
= 3/2.
dx
/
= 3/2.
an= cos nx / dx / + cos nx / dx / = =
=
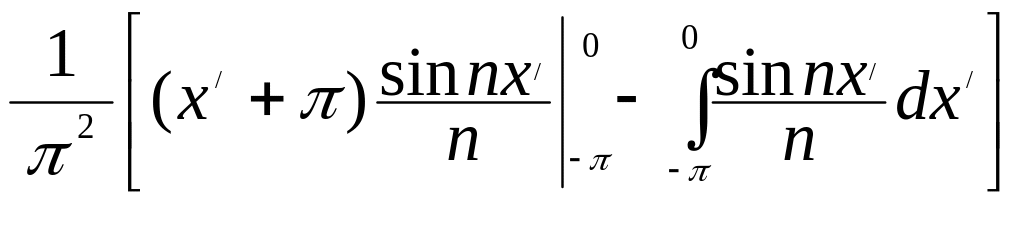 +
+
![]() =
=
![]() nx /
dx /
=
nx /
dx /
=
=
n
– четное
n
– нечетное.![]() [1–(–1)n]
=
[1–(–1)n]
=
![]()
bn
=
sin nx
/
dx
/
+
sin
nx
/
dx
/
=
![]() sin
nx
/
dx
/
= –
sin
nx
/
dx
/
= –![]() .
.
Следовательно,
f(x)
=
![]() +
+
![]() cos[(2k+1)(x–1)]
–
cos[(2k+1)(x–1)]
–
![]() sin[n(x–1)].
sin[n(x–1)].
§ 7. Разложение в ряд Фурье функций, заданных на полупериоде.
Пусть требуется разложить в ряд Фурье функцию f(x), заданную на полупериоде, т.е. в интервале (0, p) или (0,l). В этом случае можно произвольно продолжить функцию f(x) на интервал (–,0) или (–l,0) но так, чтобы образовавшаяся в этом интервале новая функция F(x), совпадающая с f(x) в интервале (0, ) или (0,l), удовлетворяла условиям основной теоремы. Разложив F(x) в ряд Фурье на интервале (-, p) или (-l,l), получим искомый ряд, представляющий f(x) в интервале (0, p) или (0,l), и не имеет значения, что он в интервале (–,0) или (–l,0) представляет какую-то другую функцию, по существу не связанную с данной функцией f(x).
В частности, f(x) можно продолжить четно на интервал (–,0) или (–l,0), значит график f(x) надо продолжить симметрично относительно оси (оу). Тогда F(x) – четная функция, и ряд будет состоять только из косинусов.
Если f(x) продолжить нечетно на интервал (–,0) или (–l,0), значит график f(x) продолжить симметрично относительно начала координат, то F(x) будет нечетной, и ряд будет состоять только из синусов.
Т.е. можно составить сколько угодно сходящихся тригонометрических рядов, представляющих в интервале (0,) или (0,l) одну и ту же функцию, а в интервале (–,0) или (–l,0) самые разнообразные функции.
Функцию, заданную на полупериоде [0; ], можно разложить в ряд синусов или ряд косинусов, продолжая на второй полупериод соответственно нечетным или четным образом.
Пример 7.
Функцию f(x)
=![]() –
–
![]() разложить в ряд косинусов на интервале
(0; ).
разложить в ряд косинусов на интервале
(0; ).
