
- •Методы физического исследования (опыт, гипотеза, эксперимент, теория)
- •Декартова система координат
- •Скорость тела при поступательном движении
- •3.Скорость тела при поступательном движении. Средняя скорость. Мгновенная скорость.
- •4. Ускорение тела при поступательном движении. Тангенциальная и нормальная
- •5. Классификация движения в зависимости от величины ускорения.
- •6.Вращательное движение.Характеристики.Угловая сокрость и усокрение.
- •8.Первый закон Ньютона. Масса. Сила. Инерциальные системы отсчета.
- •10. Третий закон Ньютона.
- •10. Третий закон Ньютона.
- •15. Движение тел с переменной массой.
- •16. Искусственные спутники Земли. Космические скорости (первая, вторая и третья).
- •Вопрос 19 момент инерции, Теорема Штейнера
- •24. Удар абсолютно упругих и неупругих тел
- •25. Тяготение. Элементы теории поля. Законы Кеплера
- •26. Опыт Кавендиша.
15. Движение тел с переменной массой.
Во многих задачах имеет место случай, когда масса тела изменяется в процессе движения за счет непрерывного отделения или присоединения вещества (ракета, реактивный самолет, платформа, нагружаемая на ходу, и др.). Определим уравнение движения такого тела.
Рассмотрим
решение этого вопроса для материальной
точки, называя ее для краткости частицей.
Пусть в некоторый момент времени ![]() масса
движущейся частицы А равна
масса
движущейся частицы А равна ![]() ,
а присоединяемая (или отделяемая) масса
имеет скорость
,
а присоединяемая (или отделяемая) масса
имеет скорость ![]() относительно
этой частицы.
относительно
этой частицы.
Введем
вспомогательную инерциальную K-систему
отсчета, скорость которой такова же,
как и скорость тела А в данный момент
.
Это значит, что в момент
частица А покоится
в этой системе. Предположим, что за
промежуток времени от
до ![]() частица А приобретает
в K-системе
импульс
частица А приобретает
в K-системе
импульс ![]() .
Этот импульс частица А получит, во-первых,
вследствие присоединения (отделения)
массы
.
Этот импульс частица А получит, во-первых,
вследствие присоединения (отделения)
массы ![]() ,
которая приносит (уносит) импульс
,
которая приносит (уносит) импульс ![]()
![]() ,
во-вторых, вследствие действия силы
,
во-вторых, вследствие действия силы ![]() со
стороны окружающих тел или силового
поля. Таким образом, можно записать, что
со
стороны окружающих тел или силового
поля. Таким образом, можно записать, что
![]()
где
знак плюс соответствует присоединению
массы, а знак минус - отделению. Оба эти
случая можно объединить, представив ![]() в
виде приращения
в
виде приращения ![]() массы
частицы А (действительно, в случае
присоединения массы
массы
частицы А (действительно, в случае
присоединения массы ![]() а
в случае отделения
а
в случае отделения![]() Тогда
предыдущее уравнение примет вид
Тогда
предыдущее уравнение примет вид
![]() .
.
Поделив
это выражение на ![]() ,
получим
,
получим
|
(4.26) |
где - скорость присоединяемого (или отделяемого) вещества относительно рассматриваемого тела.
Это
уравнение является основным
уравнением динамики материальной точки
с переменной массой.
Его называют уравнением
Мещерского.
Будучи выведенным в одной инерциальной
системе отсчета, это уравнение в силу
принципа относительности верно и в
любой другой инерциальной системе.
Заметим, что если система отсчета
неинерциальная, то под силой ![]() следует
понимать результирующую как сил
взаимодействия данного тела с окружающими
телами, так и сил инерции.
следует
понимать результирующую как сил
взаимодействия данного тела с окружающими
телами, так и сил инерции.
Последний
член уравнения (4.26) носит
название реактивной
силы: ![]() .
Эта сила возникает в результате действия
на данное тело присоединяемой (или
отделяемой) массы. Если масса присоединяется,
то
.
Эта сила возникает в результате действия
на данное тело присоединяемой (или
отделяемой) массы. Если масса присоединяется,
то ![]() и
вектор
и
вектор ![]() совпадает
по направлению с вектором относительной
скорости; если же она отделяется, то
совпадает
по направлению с вектором относительной
скорости; если же она отделяется, то ![]() и
вектор
противоположен
вектору
.
и
вектор
противоположен
вектору
.
Уравнение
Мещерского по своей форме совпадает в
основным уравнением динамики материальной
точки постоянной массы: слева - произведение
массы тела на ускорение, справа -
действующие на него силы, включая
реактивную силу. Однако в случае
переменной массы нельзя внести массу
под
знак дифференцирования и представить
левую часть уравнения как производную
по времени от импульса, так как ![]() .
.
Отметим два важных частных случая.
1.
Если ![]() ,
т. е. масса присоединяется или отделяется
без скорости относительно тела, то
,
т. е. масса присоединяется или отделяется
без скорости относительно тела, то ![]() ,
и уравнение (4.26) принимает
вид
,
и уравнение (4.26) принимает
вид
|
(4.27) |
где ![]() -
масса тела в данный момент времени. Это
уравнение определяет, например, движение
платформы, из которой свободно высыпается
песок.
-
масса тела в данный момент времени. Это
уравнение определяет, например, движение
платформы, из которой свободно высыпается
песок.
2.
Если ![]() ,
т. е. присоединяемая масса неподвижна
в выбранной системе отсчета или отделяемая
масса становится неподвижной в этой
системе, то уравнение (4.26) принимает
другой вид
,
т. е. присоединяемая масса неподвижна
в выбранной системе отсчета или отделяемая
масса становится неподвижной в этой
системе, то уравнение (4.26) принимает
другой вид
![]()
или
|
(4.28) |
Иначе говоря, только в этом частном случае действие силы определяет изменение импульса тела с переменной массой. Данный случай реализуется, например, при движении платформы, нагружаемой сыпучим веществом из неподвижного бункера.
Рассмотрим пример на применение уравнения Мещерского.
Пример.
Ракета движется в инерциальной K-системе
отсчета в отсутствие внешнего силового
поля, причем так, что газовая струя
вылетает с постоянной относительно
ракеты скоростью![]() .
Определить зависимость скорости ракеты
от ее массы
,
если в момент старта начальная масса
ракеты равна
.
Определить зависимость скорости ракеты
от ее массы
,
если в момент старта начальная масса
ракеты равна ![]() .
.
В
данном случае ![]() и
из уравнения (4.26) следует
и
из уравнения (4.26) следует
![]()
Проинтегрировав это выражение с учетом начальных условий, получим
![]()
где
знак минус показывает, что вектор
скорости ракеты ![]() противоположен
по направлению вектору скорости
вытекающих газов
.
Эта формула носит специальное название
- формула Циолковского. Отсюда видно,
что конечная скорость ракеты в случае
противоположен
по направлению вектору скорости
вытекающих газов
.
Эта формула носит специальное название
- формула Циолковского. Отсюда видно,
что конечная скорость ракеты в случае ![]() не
зависит от времени сгорания
топлива:
определяется
только отношением начальной массы
ракеты
к оставшейся массе m.
не
зависит от времени сгорания
топлива:
определяется
только отношением начальной массы
ракеты
к оставшейся массе m.
Заметим, что если бы вся масса горючего была одновременно выброшена со скоростью относительно ракеты, то скорость последней оказалась бы иной. Действительно, если ракета вначале покоилась в выбранной инерциальной системе отсчета, а после одновременного выброса всего горючего приобрела скорость , то из закона сохранения импульса для системы ракета - гoрючее следует
![]() ,
,
где ![]() -
скорость горючего относительно данной
системы отсчета. Отсюда определяем
скорость ракеты
-
скорость горючего относительно данной
системы отсчета. Отсюда определяем
скорость ракеты
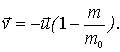
Скорость
ракеты
в
этом случае оказывается меньше, чем в
предыдущем при условии, что отношение
масс ![]() одинаково.
В этом нетрудно убедиться, сравнив
характер зависимости
от
отношения масс в обоих случаях. С
ростом
одинаково.
В этом нетрудно убедиться, сравнив
характер зависимости
от
отношения масс в обоих случаях. С
ростом ![]() в
первом случае, когда вещество отделяется
непрерывно, скорость
ракеты,
в соответствии с первой формулой, растет
неограниченно, во втором же случае,
когда вещество отделяется одновременно,
скорость
в
первом случае, когда вещество отделяется
непрерывно, скорость
ракеты,
в соответствии с первой формулой, растет
неограниченно, во втором же случае,
когда вещество отделяется одновременно,
скорость ![]() стремится
к пределу, равному
стремится
к пределу, равному ![]()
