1.2. Анализ уравнений продольного возмущенного движения

В связанной системе координат плоскость симметрии самолета хОу называется продольной. В этой плоскости действует тангенциальная сила R _x, нормальная сила R _y и момент тангажа М_z. Перемещение центра масс и вращение самолета вокруг него в плоскости симметрии называются продольным движением и характеризуется скоростью полета V, углами атаки  и тангажа .

Продольное и боковое движения взаимно связаны, но в случае малых возмущений применяют допущение, что при малых возмущениях и одной и той же скорости полета продольные силы и моменты не зависят от кинематических параметров бокового движения, т.е.

В связи с этим в уравнениях системы (4.3), описывающих движение в продольной плоскости, исчезнут члены, содержащие вариации кинематических параметров бокового движения.

Учтем, что для современных транспортных самолетов центробежный момент инерции J_xy очень мал по сравнению с осевыми моментами инерции J_x, J_y, J_z. Исключим переменную _я, поскольку _я  d/dt. Отбросим ввиду малости члены, содержащие произведения углов атаки и скольжения на вариации кинематических параметров. Тогда систему дифференциальных уравнений для продольного возмущенного движения, в процессе которого на самолет действуют как управляющие, так и внешние возмущения, закон изменения которых во времени известен, можно представить следующим образом (смотри систему уравнений на с.31):

(4.4)

Последнее уравнение системы выражает кинематическую связь между углами тангажа, атаки и наклона траектории.

Если предположить, что управляющих и внешних возмущений нет, то для возмущенного движения, обусловленного возмущением только начальных кинематических параметров, из-за наличия вариаций кинематических параметров претерпевают изменения основные силы и моменты, действующие на самолет. Для этого случая система уравнений (4.4) записывается так:

(4.5)

1.3. Анализ решения системы дифференциальных уравнений возмущенного движения

Метод анализа основан на том, что исследуется система линейных дифференциальных уравнений. Для упрощения записи систему уравнений (4.4) приведем к следующей форме:

(4.6)

Система (4.6) является линейными неоднородными уравнениями с постоянными коэффициентами, так как а_i0  0. Когда управление зажато и возмущающих факторов нет, то а_i0 = 0. Последнее соответствует собственному возмущенному движению самолета.. Значения коэффициентов а_ij приведены в табл. 1.

Решение уравнений может быть получено методами, изучаемыми в курсе высшей математики. Например, решение уравнений (4.6) можно получить в виде

(4.7)

где Р_i – корни характеристического уравнения, составленного из коэффициентов при неизвестных в уравнениях системы (4.6):

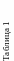
а´ij		а'11 = m а''22=-mV а'23=mV а''33=Jz а'33=-Mz а'32=-Mz
j	0	Rxвв + Rxнн + Rxээ + Rxрдрд + Rxв Ryвв + Ryв Mzвв + Mzрдрд + Mzв
	4	o 0 0
	3	-Rx -Ry 0
	2	-Rx -RУ  -Mz
	1	-RxV -RyV -MzV
аij		а1j а2j а3j

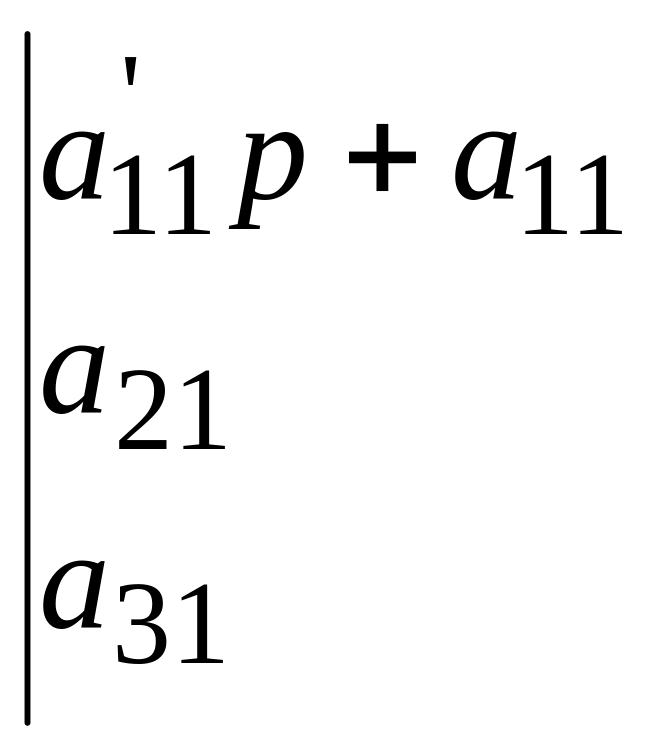
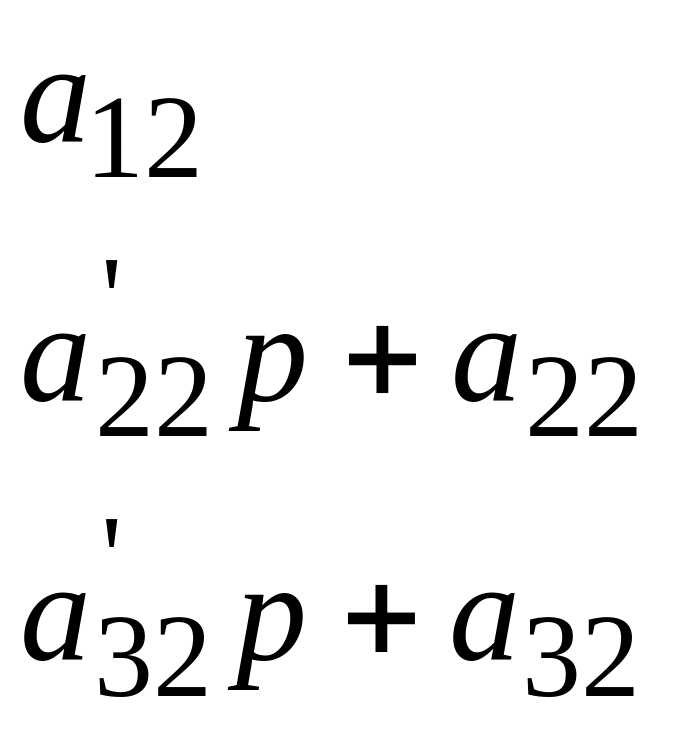
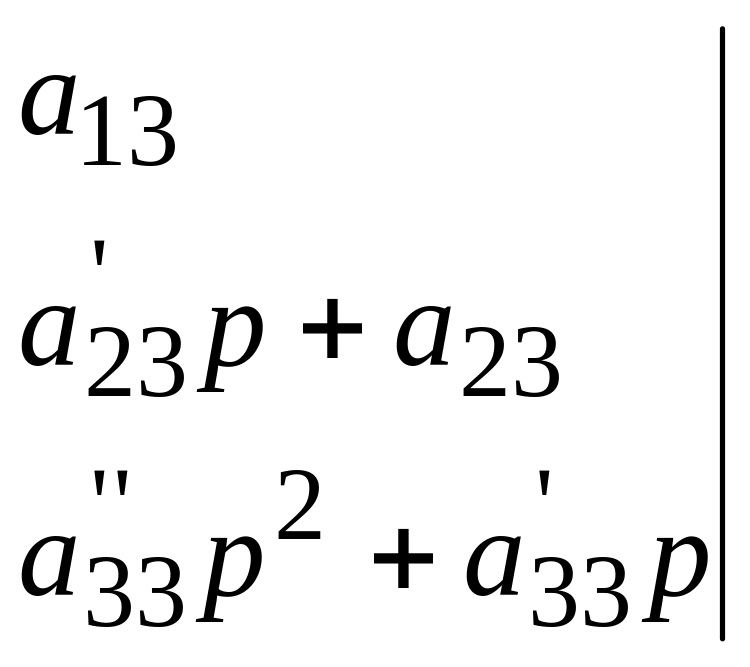(4.8)

Функции f_V(t), f_(t) и f_(t) в решении (4.7) являются частными решениями системы (4.6) с правой частью, отличной от нуля.

Величины А_i, В_i, С_i – постоянные интегрирования, зависящие от начальных условий. Ограничимся только анализом свойств решения, не рассматривая весь процесс отыскания решения.

Если раскрыть определитель характеристического уравнения (4.8), то получим обычное алгебраическое уравнение четвертой степени относительно p:

(4.9)

где значения коэффициентов определяются по формулам

(4.10)

Из решения системы(4.8) видно, что при f_V=f_=f_=0 вариации параметров движения с течением времени могут возрастать, убывать или оставаться постоянными в зависимости от значений показателей р_i, которые как корни характеристического уравнения (4.9) зависят от аэродинамических и массовых характеристик самолета.

Так как коэффициенты характеристического уравнения (4.9) а₀,а₁,а₂, а₃,а₄ являются действительными величинами, то в соответствии с основной теоремой алгебры корни характеристического уравнения р₁, р₂, р₃, р₄ могут быть действительными или попарно сопряженными комплексными числами. Если все корни характеристического уравнения действительные, то зависимость вариаций параметров движения от времени носит апериодический характер и возмущенное движение представляет собой сумму четырех накладывающихся одно на другое частных апериодических движений. Если при этом все корни р₁, р₂, р₃, р₄ отрицательны, то вариации скорости, углов атаки и тангажа с течением времени убывают, стремясь к 0 при t, и возмущенное движение асимптотически устойчивое; если же хотя бы один из этих корней положителен, то вариации параметров движения стремятся к бесконечности при t  и возмущенное движение асимптотически неустойчивое.

Если корни характеристического уравнения являются комплексными, взаимно сопряженными величинами, то зависимости вариации параметров движения от времени носят колебательный характер ( возмущенное движение представляет собой наложение двух колебательных движений ).

Установлено, что для асимптотической устойчивости продольного невозмущенного движения необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательные действительные части.

Для того, чтобы все корни алгебраического уравнения

имели, согласно теореме Гурвица, отрицательные вещественные части, необходимо и достаточно выполнить следующие условия:

₁  , ₂  ,…, _n  , (4.11)

где ₁ = а₁, ₂ = ,

_n = .

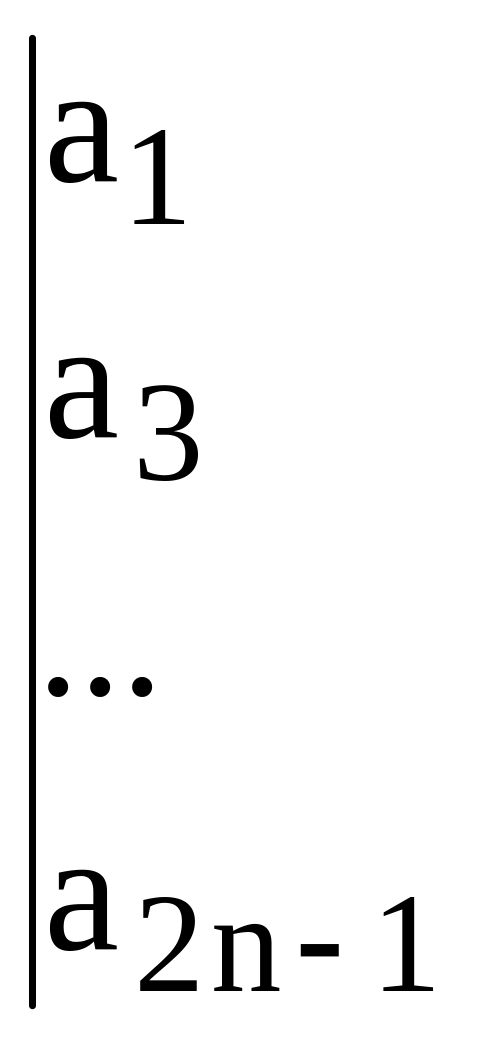
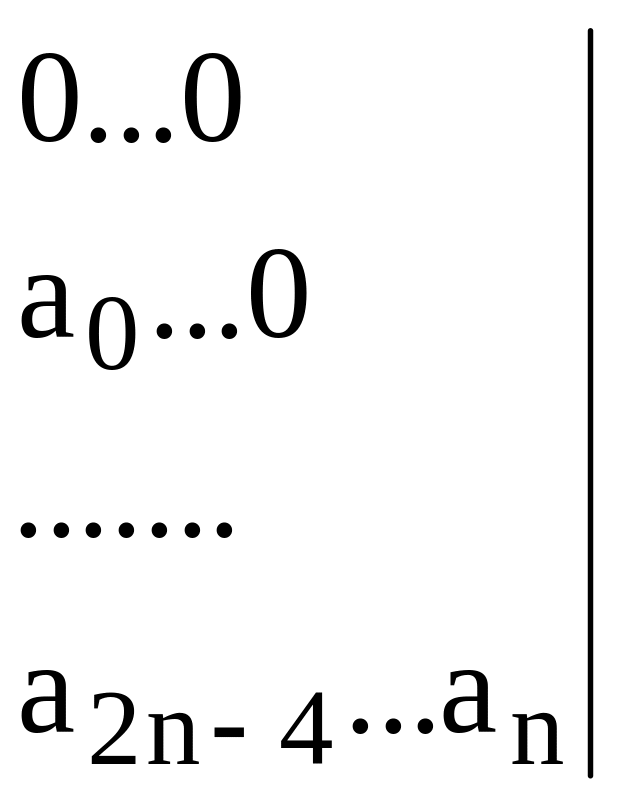Для уравнения четвертой степени условия (4.10) принимают вид

Δ₀  , Δ ₁  , Δ ₂  , Δ ₃  , Δ ₄  , (4.12)

₃ = = а₃(а₁ а₂ – а₀ а₃) – а₄ а²₁  0.

Выражение (4.11) носит название критерия Рауса – Гурвица.

Заменив в соотношениях (4.11) знаки неравенства знаками равенства, получим границы устойчивости возмущенного движения. Эти условия не отвечают на вопрос о степени устойчивости или неустойчивости, о характере возмущенного движения.

1.4. Общие свойства продольного возмущенного движения

При малых начальных возмущениях кинематических параметров ΔV, Δ α, Δφ, ω_z продольного невозмущенного движения продольное возмущенное движения описывается линейными дифференциальными уравнениями (4.4). Коэффициентами при неизвестных в этих уравнениях являются частные производные от проекций R_x1, R_y1 главного вектора и M_z1 главного момента сил, действующих на самолет.

Методы определения R_x1, R_y1 и M_z1 приведены в [1]. Например, проекции R_x1, R_y1 на оси связанной системы координат для прямолинейного полета в вертикальной плоскости без крена и скольжения определяются соотношениями

,

,

где Х₁= и Y₁= - тангенциальная и нормальные силы (для малых углов атаки с_у1 ≈ с_у; с_х1 = с_х - αс_у); Р_у1 – поперечная составляющая тяги, обусловленная несовпадением вектора скорости полета с осью ОХ₁; Р_х1 ≈ Р из-за малости угла φ_дв.

Частная производная от R_x1 по скорости определится

,

а частная производная Р^V – высотно-скоростным характеристикам двигателя. Величина С^M_x1 практически равна нулю при М < М_кр, затем она растет и достигает максимума при числе М, предшествующем чисто сверхзвуковому режиму обтекания самолета. Далее она убывает и становится отрицательной.

Частную производную от R^α_х1 при условии, что тангенциальная составляющая тяги двигателей не зависит от угла атаки, можно записать в виде

R^α_x1= - .

Величина с^α_х1 находится численным дифференцированием экспериментально получаемой зависимости с_х1=f(α).

Так как тяга двигателей и сила лобового сопротивления от угла тангажа не зависят, то R^φ_x1= - G cosφ.

Частные производные находятся как приращения тангенциальной силы при отклонении рулей на единичный угол, например, = - .

Величина определяется из характеристик двигателя, связывающих угловое положение рычага управления двигателяем с тягой двигателя.

Частные производные от R_у на ось Оу₁ при условии, что величина проекции силы тяги на ось Оу₁ не изменяется при изменении скорости, имеют вид

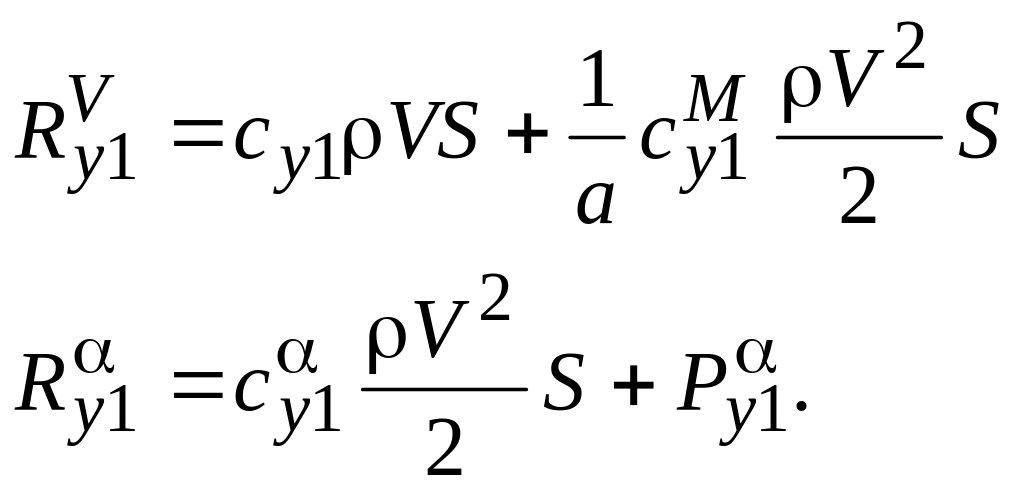
Для самолета с ТРД Р^α_у1 = m_вV, где m_в – секундный расход воздуха двигателя.

Производная от R_у по углу тангажа равна

Частная производная может быть записана так

= ,

где = ,

= .

Решение уравнений возмущенного движения позволяет найти кинематические характеристики α, V, φ, ω_z как функции времени. Расчеты показывают, что для реальных компоновок самолетов возмущенное движение статически устойчивого самолета определяется характером основного движения и может состоять либо из двух колебательных движений, либо из одного колебательного и двух апериодических движений. В случае горизонтального движения возмущенное обычно складывается из двух колебательных движений; для прямолинейного с подъемом – из одного колебательного и двух апериодических движений.

В решении уравнений (4.4) среди комплексных корней характеристического уравнения (4.9) можно выделить по модулю два больших и два малых корня. Установлено, что большие комплексные сопряженные корни определяют короткопериодическое движение, а малые – длиннопериодическое. Длиннопериодическое (медленное) движение связано в основном с поступательным перемещением самолета в пространстве, а короткопериодическое – с вращательным.

Длиннопериодическое движение может быть вовремя замечено и устранено экипажем самолета, а короткопериодическое движение настолько быстро, что контролировать и корректировать его чрезвычайно трудно.

Физической причиной возникновения двух видов движения является значительная инертность летательного аппарата к искривлению траектории движения, что обусловливает медленное изменение параметров, характеризующих траекторию движения (ΔV,Δφ) и относительно быстрое протекание вращательных движений.

Типичная зависимость параметров продольного возмущенного движения от времени показана на рис. 4.1.

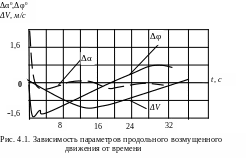
Быстропротекающее движение играет значительную роль в оценке динамических свойств летательного аппарата. Особое значение оно приобретает для аппарата, управляемого человеком, поскольку человеку очень трудно контролировать и корректировать это движение.

Длиннопериодическое – медленное движение, протекает в течение длительного времени, пилот вполне успевает машинально корректировать это движение.

Изменение параметров на начальном этапе возмущенного движения представлено на рис. 4.2.

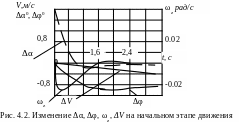
Количественными критериями, характеризующими возмущенное движение, являются период колебаний, время уменьшения амплитуды колебаний вдвое, число колебаний до практически полного затухания.

Из высшей математики известно, что устойчивость – это свойство системы возвращаться в исходное установившееся состояние после выхода из него в результате какого-либо воздействия.

Устойчивость линейной системы определяется характером переходного процесса. Если переходный процесс с течением времени затухает, то система устойчива и наоборот. Само качество переходных процессов линейных систем определяется следующими основными показателями (см. рис. 4.3):

временем переходного процесса t_пер – временем, по истечении которого переходная функция h(t) отличается от установившегося значения h_уст не более чем на 5% величины h_уст;

временем срабатывания t_ср – временем, по истечении которого переходная функция h(t) в первый раз достигает своего установившегося значения h_уст. Время срабатывания характеризует быстродействие системы;

перерегулированием σ – отношением максимального превышения переходной функции над установившимся к установившемуся значению:

Величина σ характеризует колебательность переходного процесса.