Розділ іі. Невластиві інтеграли Рімана §1. Теоретичні питання.

1. Означення і основні властивості невластивого інтеграла першого роду: від обмеженої функції по необмеженому проміжку інтегрування . Головне значення невластивого інтеграла першого роду. Приклади.

2. Теорема конгруентності (порівняння) для невластивих інтегралів першого роду від невід’ємних функцій.

3. Теорема про абсолютну збіжність невластивого інтеграла.

4. Теорема Діріхлє про умовну збіжність невластивого інтеграла першого роду.

5. Теорема Абеля про умовну збіжність невластивого інтеграла першого роду.

6. Означення невластивого інтеграла другого роду: від необмеженої функції по обмеженому проміжку інтегрування. Головне значення інтеграла другого роду. Приклади.

7. Властивості невластивого інтеграла другого роду: критерій Коші збіжності, заміна змінної, теорема конгруентності.

8. Зведення невластивого інтеграла другого роду до невластивого інтеграла першого роду, абсолютна збіжність, теореми Діріхлє та Абеля для невластивого інтеграла другого роду.

9. Збіжність , інтегралів Френеля на проміжку .

10. Гама–функція Ейлера: означення і доведення збіжності.

11. Основна властивість гама–функцій, узагальнення факторіала, графік гама–функцій ( ).

12. Бета–функція Ейлера: означення, доведення інтегрального представлення , .

13. Зв’язок між гама та бета–функцією , . Збіжність бета–функції.

14. Довести, що (інтеграл Пуассона).

15. Довести,що , .

§ 2. Означення невластивих інтегралів першого і другого роду. Збіжність невластивого інтеграла від невід’ємної функції.

Означення (невластивого інтеграла першого роду від обмеженої функції по необмеженому проміжку інтегрування):

Припустимо, що

1) , ;

2) , де ( обмежена на ).

Наступну границю називають невластивим інтегралом першого роду і позначають .

(Символ називають особливою точкою невластивого інтеграла). Якщо ця границя існує і скінченна, тоді інтеграл називають збіжним. У випадку, коли вона дорівнює нескінченості або не існує, інтеграл називають розбіжним.

Подібно ,

.

В останньому випадку інтеграл збігається, якщо обидві границі існують і скінченні.

Головним значенням (valeur principale) називають

.

Приклад 10. Дослідити на збіжність , де .

■ Згідно з означенням:

При :

При : ;

.

Отже, .■

Невластивий інтеграл зберігає основні властивості визначеного інтеграла: 1) лінійності і адитивності відносно проміжку інтегрування;

2) теореми заміни змінної і інтегрування частинами;

3) формулу Ньютона-Лейбніца: якщо для існує первісна на ( ), тоді .

При дослідженні інтеграла на збіжність, за умови невід’ємності підінтегральної функції, використовують

Теорему (порівняння).

Якщо 1) для ;

2) для , тоді

1. якщо збігається , тоді збігається і ;якщо розбігається , тоді розбігається .

2. якщо ( 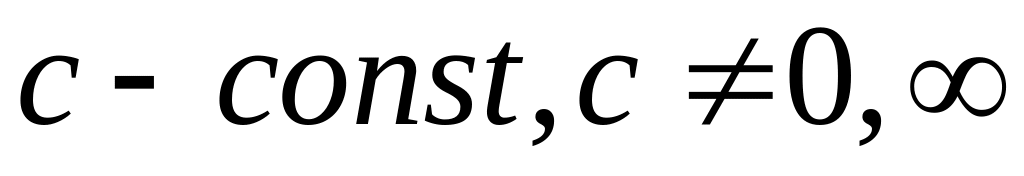), тоді і збігаються і розбігаються одночасно.

3. якщо ( ), тоді при інтеграл збігається, а при інтеграл розбігається.

Приклад 11. Дослідити на збіжність 1) ; 2) .

■ 1) – інтеграл збігається.

2) – інтеграл розбігається. ■

Означення (невластивого інтеграла другого роду від необмеженої функції по обмеженому проміжку інтегрування).

Припустимо, що

1) ;

2) ;

3) , де , тобто .

Наступну границю називають невластивим інтегралом другого роду і позначається .

Точку називають особливою точкою невластивого інтеграла.

Подібно, якщо є особливою точкою, маємо .

Якщо , є особливою точкою інтеграла, тоді .

Якщо кожна з цих границь існує і скінченна, то інтеграл називають збіжним, в протилежному випадку – розбіжним.

Головним значенням (valeur principale) з особливою точкою , називають .

Приклад 12. Дослідити на збіжність , де .

■ При даний інтеграл є звичайним інтегралом Рімана , а отже збіжним.

При точка є особливою точкою невластивого інтеграла другого роду.

При : .

При :

При інтеграл збігається;

При інтеграл розбігається.

Отже, .■

Приклад 13. Знайти

■ є особливою точкою інтеграла другого роду. Згідно з означенням

. ■

Зауважимо,що кожний з інтегралів є розбіжним.

Властивості сформульовані для невластивих інтегралів першого роду вірні і для невластивих інтегралів другого роду. Сформулюємо випадок ІІІ теореми порівняння:

ІІІ′. Якщо є невластивим інтегралом другого роду з особливою точкою і ( ), тоді при : розбігається, а при збігається.