Передмова

Методичні вказівки складено до двох розділів математичного аналізу: “Визначений інтеграл і його застосування” та “Невластиві інтеграли Рімана”. Вони містять теоретичні питання до колоквіумів, основні означення і формули, які використовуються при розв’язанні задач, розв’язки типових задач, завдання типової розрахункової роботи і відповіді до цих завдань. У додатку наведено таблицю значень гама функції (див. Е. Янке, Ф. Эмде, Ф. Леш. Специальные функции.– М.: “Наука”, 1968.– с. 342). Робота виконується у другому семестрі і може бути запропонована як студентам фізико–математичного факультету так і студентам факультету інформатики та обчислювальної техніки. Кожен студент готує та здає усно теоретичний матеріал на колоквіумі і у письмовій формі завдання типової роботи, вказані викладачем. Зошит з розв’язаними задачами повинен бути зданий викладачеві, який проводить практичні заняття, до контрольної роботи.

Студент, який не здав колоквіум і типову роботу, не допускається до екзамену, як такий, що не виконав навчальний графік.

Розділ і. Визначений інтеграл Рімана і його застосування § 1. Теоретичні питання

1. Означення інтеграла Рімана, необхідна умова його існування. Функція Діріхлє, яка є обмеженою, але не інтегрованою за Ріманом.

2. Суми Дарбу, їх властивості. Означення інтегралів Дарбу.

3. Необхідна і достатня умова існування інтеграла Дарбу. Означення коливання функції на сегменті.

4. Теорема Дарбу про необхідну і достатню умову існування інтеграла Рімана.

5. Теорема про інтегрованість функції, неперервної на сегменті.

6. Теорема про інтегрованість функції, неперервної на сегменті за винятком скінченого числа точок розриву першого роду.

7. Лінійність і адитивність відносно проміжку інтегрування визначеного інтеграла.

8. Теореми про інтегрування нерівностей. Груба оцінка визначеного інтеграла.

9. Теорема про середнє для визначеного інтеграла.

10. Рівномірна збіжність послідовності функцій. Теорема про граничний перехід під знаком визначеного інтеграла.

11. Визначений інтеграл як функція змінної верхньої границі інтегрування, його властивості. Достатні умови існування невизначеного інтеграла.

12. Зв’язок між визначеним і невизначеним інтегралами: формула Ньютона–Лейбніца. Формула Лейбніца. Інтегрування періодичної функції по періоду.

13. Формули заміни змінної і інтегрування частинами у визначеному інтегралі. Інтегрування парної та непарної функції у симетричних границях.

14. Формула Тейлора із залишковим членом у інтегральній формі.

15. Обчислення інтегралів 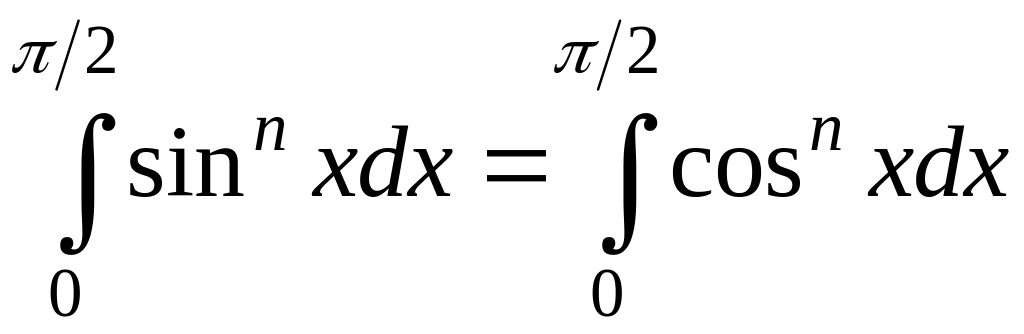( ). Формула Валліса.

16. Застосування визначеного інтеграла в геометричних задачах: знаходження площі плоскої фігури і об’ємів тіл.

17. Означення кривої і векторної функції. Границя і неперервність векторної функції.

18. Похідна, диференціал, теорема про середнє для векторної функції.

19. Два означення довжини дуги. Означення гладкої дуги. Теорема про спрямлюваність гладкої дуги.

20. Еквівалентність двох означень довжини гладкої незамкненої дуги. Параметризація гладкої дуги, натуральний параметр.

21. Теорема про еквівалентність в малому довжини гладкої дуги довжині хорди, що її стягує.

22. Формули обчислення довжини гладкої дуги.

23. Еліптичні функції Лежандра (1, 2, 3 роду). Знаходження площі поверхні обертання.

24. Криволінійні інтеграли першого роду (по довжині дуги): означення і формули обчислення.

25. Застосування визначеного інтеграла в задачах фізики.

§ 2. Визначений інтеграл: означення, формула Ньютона–Лейбніца. Основні теореми і формули, які використовуються при розв’язанні задач

Таблиці похідних та невизначених інтегралів

1.	1.
2.	2.
3.	3.
4.	4.
5.	5. , ( )
6.	6. , ( )
7.	7. , ( )
8.	8. (у точках неперервності )
9.	9. (у точках неперервності )
10.	10. , ( , )
11.	11. , ( , )
12.	12. , ( )
13.	13. , ( , )
14.	14. ,
15.	15. ,
16.	16. ,
17.	17. ,
	18. ,
(	19. ,
20. , (у точках неперервності )
21. , (у точках неперервності )
22.

Деякі формули, що використовуються при інтегруванні

; ; ; ;
;		;
;		;
;		;
;		;
;		;
;		;
;		;
;	;		.

Означення визначеного інтеграла. Будемо вважати, що:

1. функцію означено на сегменті ;

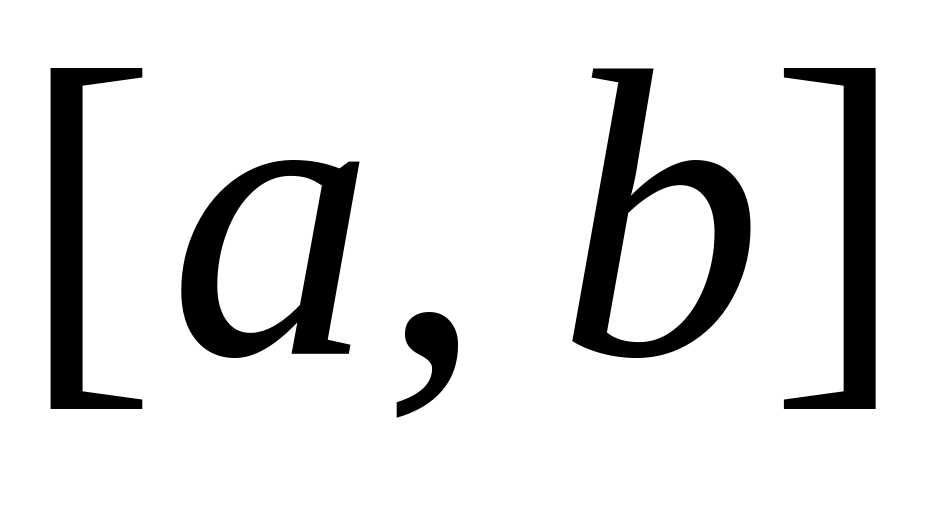2. поділ сегмента ( 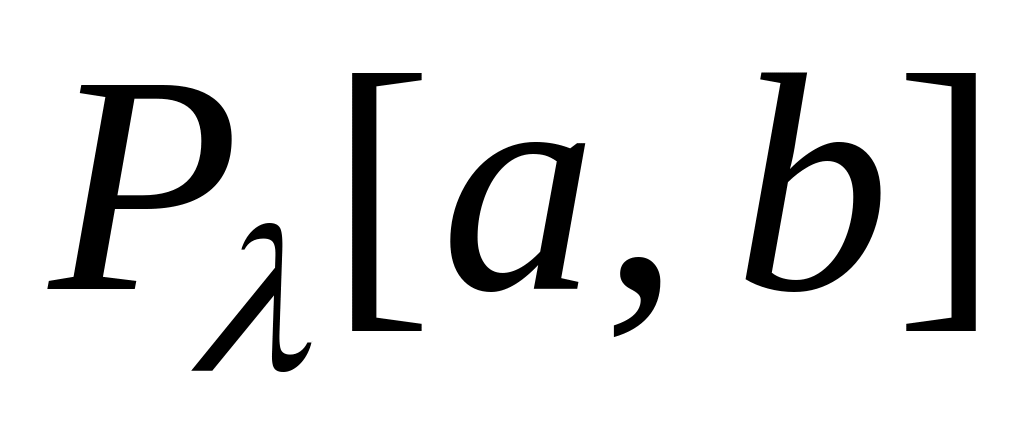) включає наступні умови: поділимо довільним чином на п частин 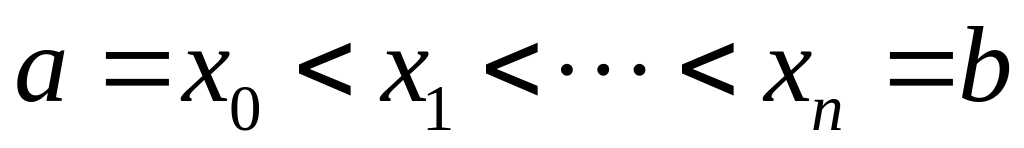; виберемо 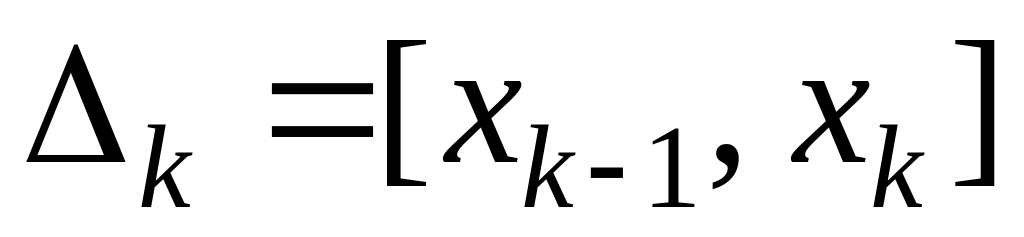, знайдемо його довжину ; виберемо довільну точку і позначимо ( );

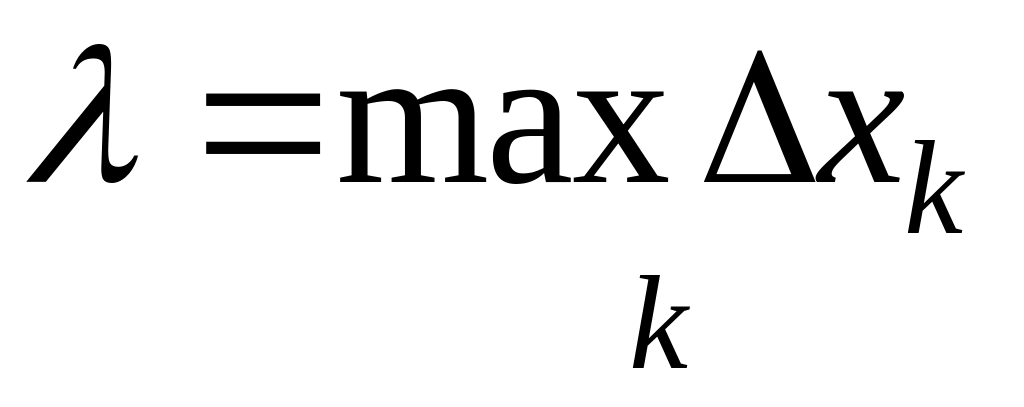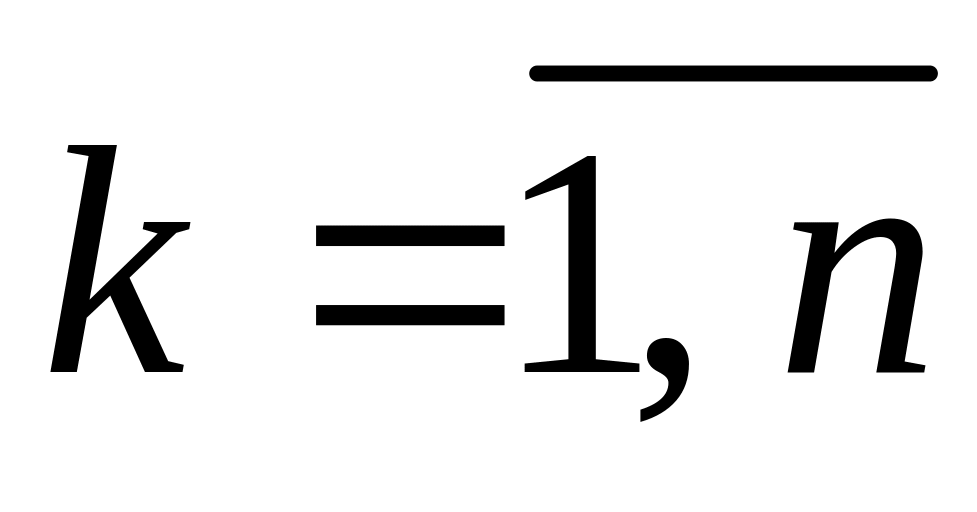3. побудуємо інтегральну суму Рімана функції на при заданому :

.

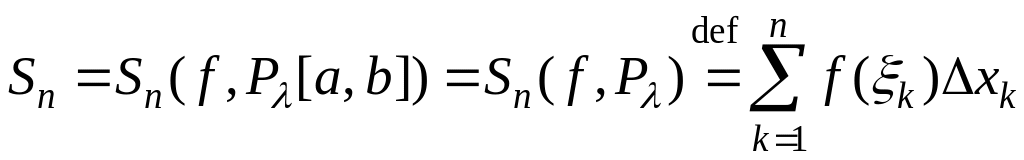Функцію називають інтегрованою за Ріманом на , якщо

і не залежить від , вибору точки і способу прямування . Цю границю називають визначеним інтегралом Рімана функції на і позначають , де а – нижня ( – верхня) границі інтегрування.

Множину функцій, інтегрованих за Ріманом на позначають .

Необхідною умовою існування визначеного інтеграла є обмеженість функції на .

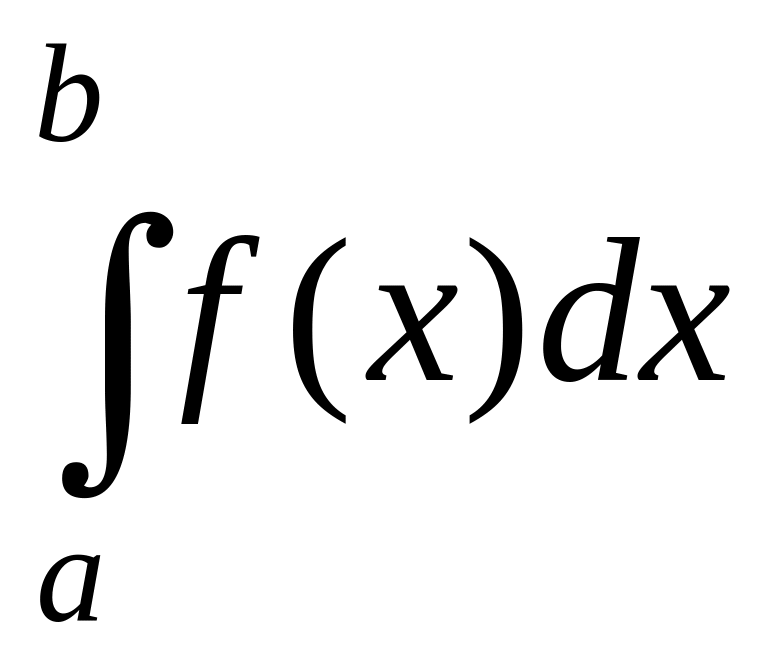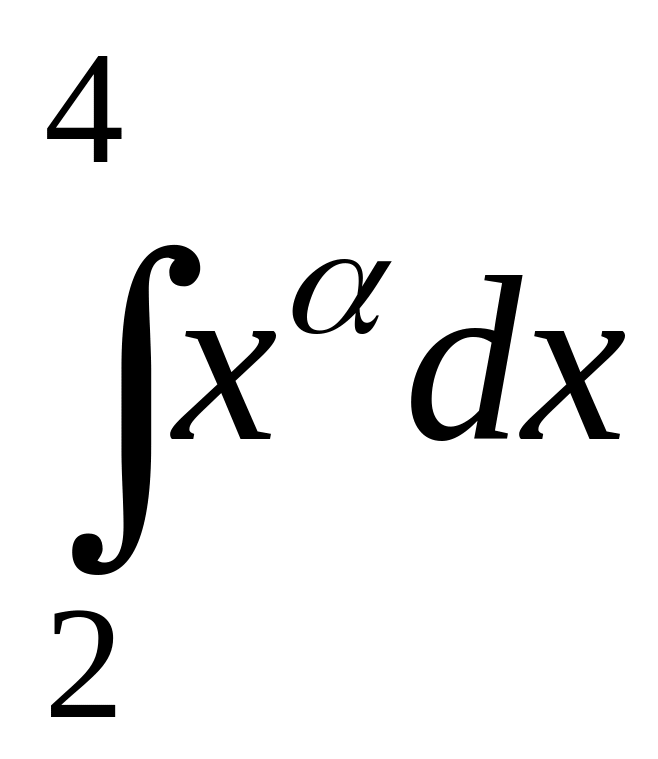Приклад 1. Побудувати інтегральну суму для функції на проміжку і, користуючись означенням визначеного інтеграла, знайти , якщо а) ; б) , де .

■ а) Поділимо проміжок на п рівних частин, тоді , , . Виберемо точку ( ), тоді . Запишемо інтегральну суму . Остання сума є сумою п членів геометричної прогресії 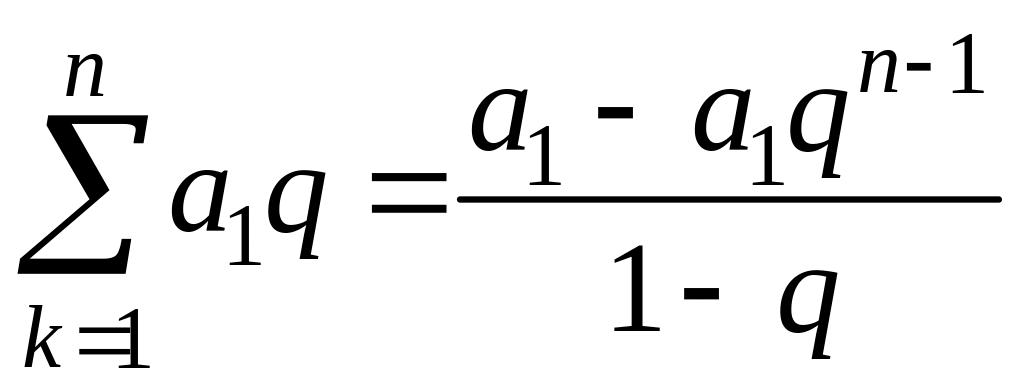, де .

Таким чином

.

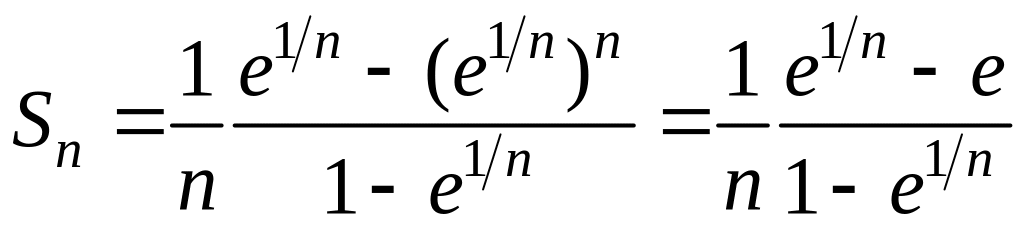Використовуючи еквівалентність функцій коли знайдемо

.

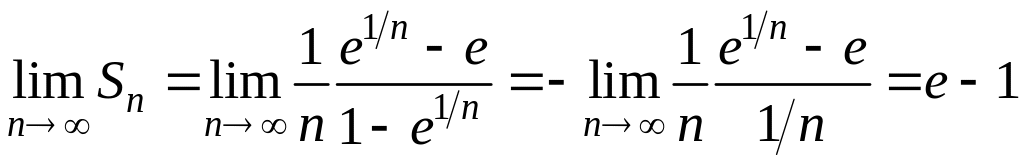Відповідь: 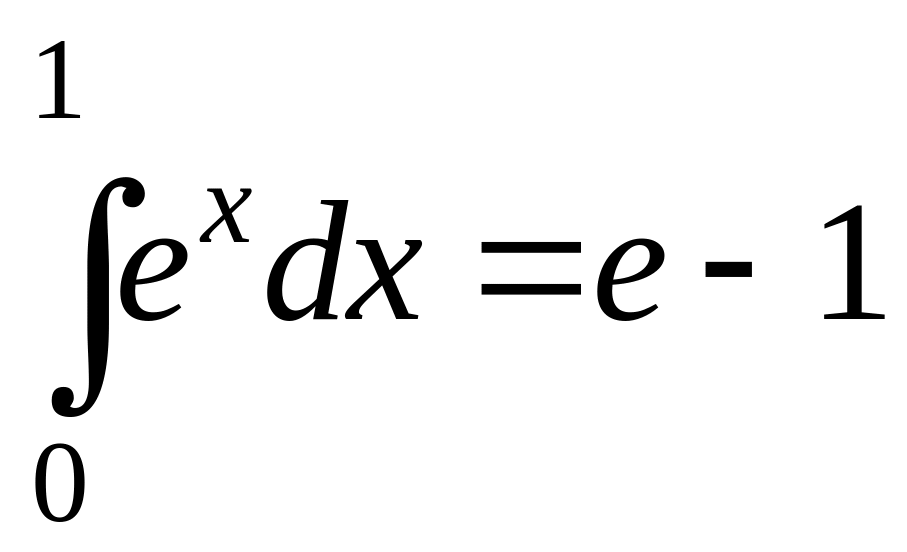для вибраного поділу .

б) Поділимо проміжок на п частин так, що 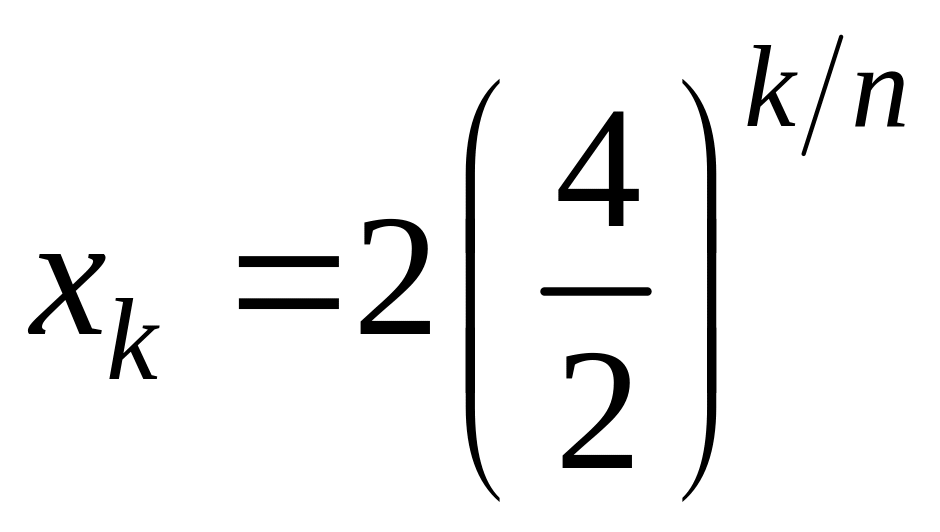( ) утворюють геометричну прогресію з .

Тоді коли .

Виберемо точку ( ) і запишемо інтегральну суму

.

.

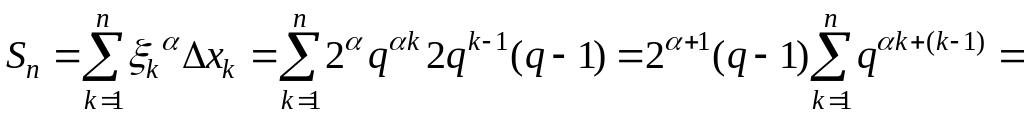
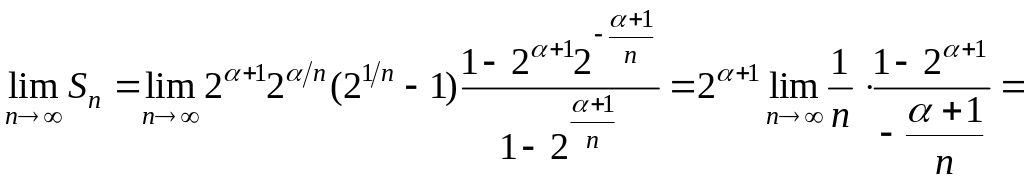
Відповідь: 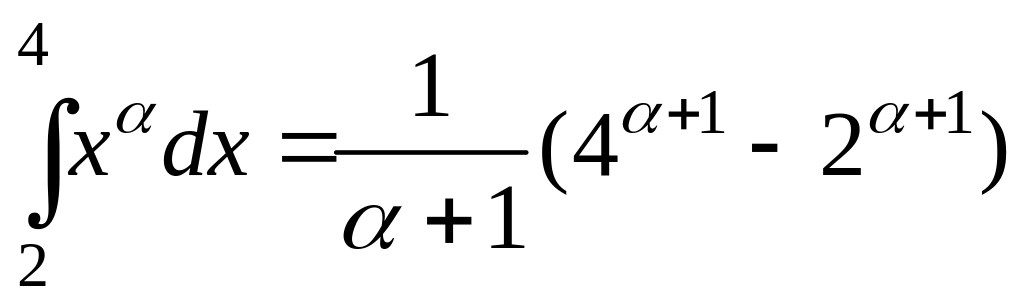для вибраного поділу .
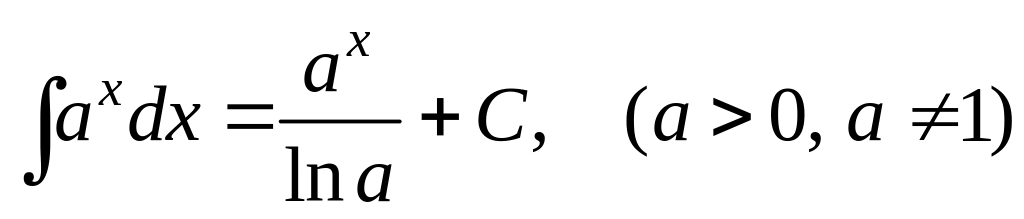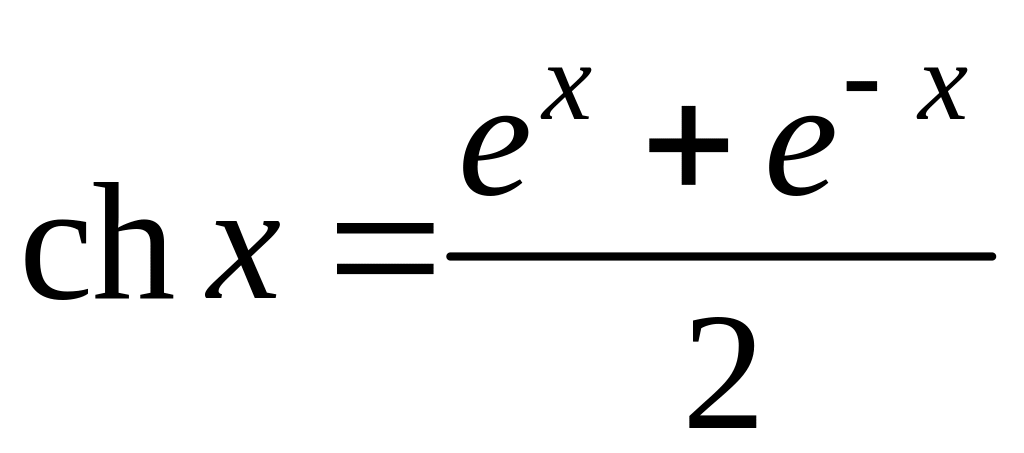
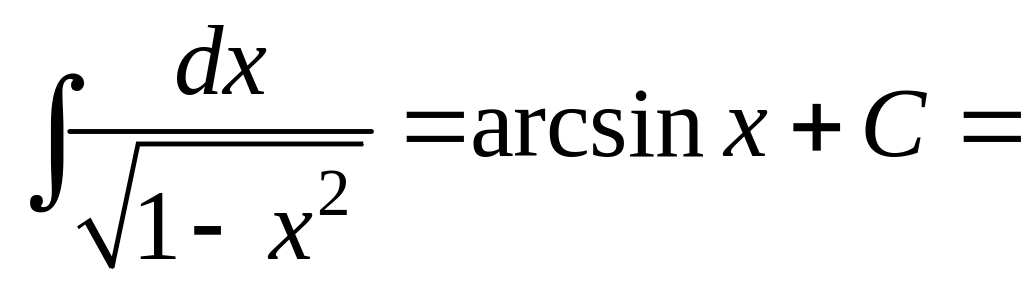
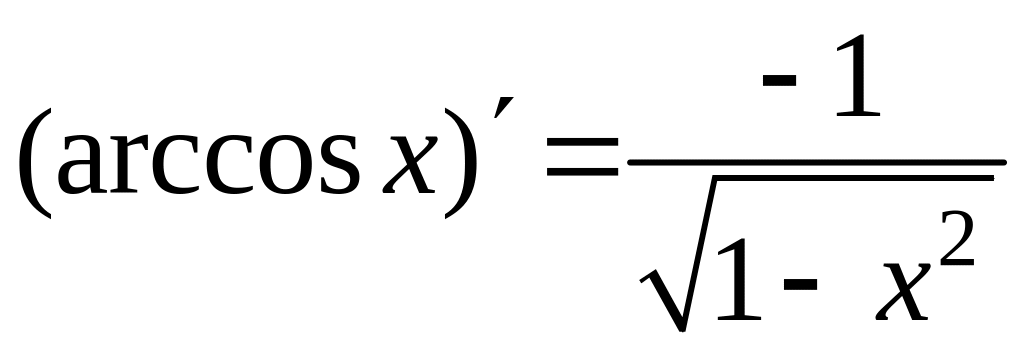
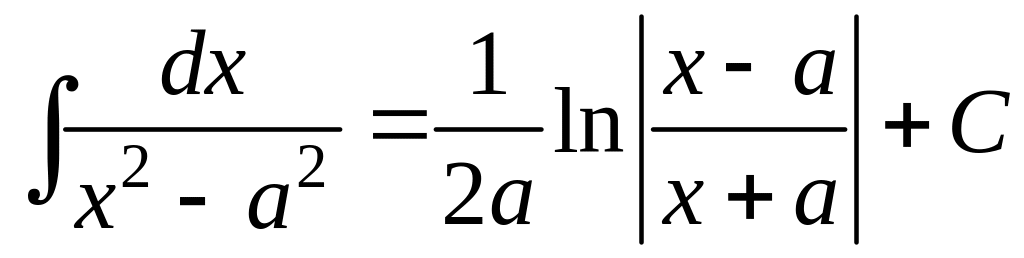
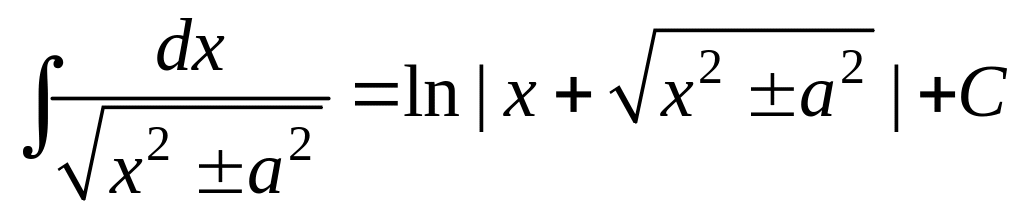
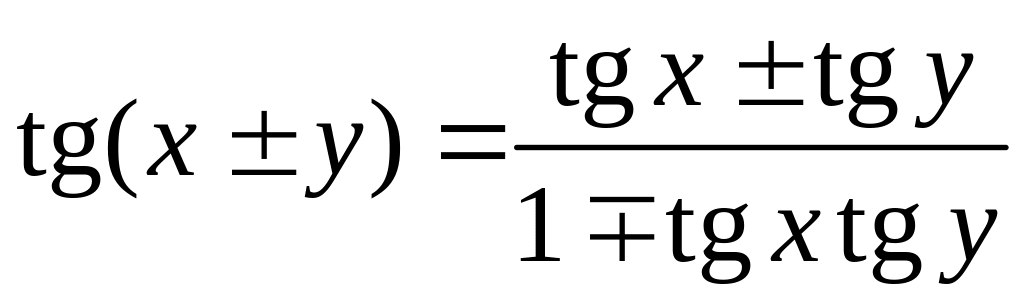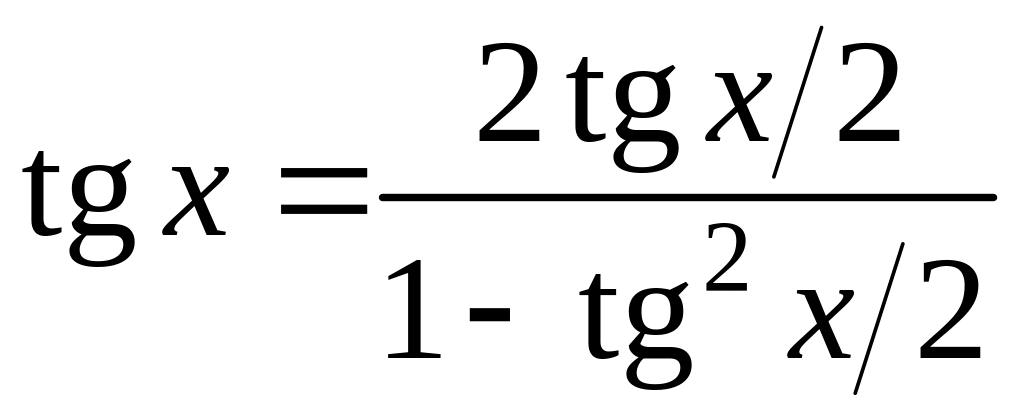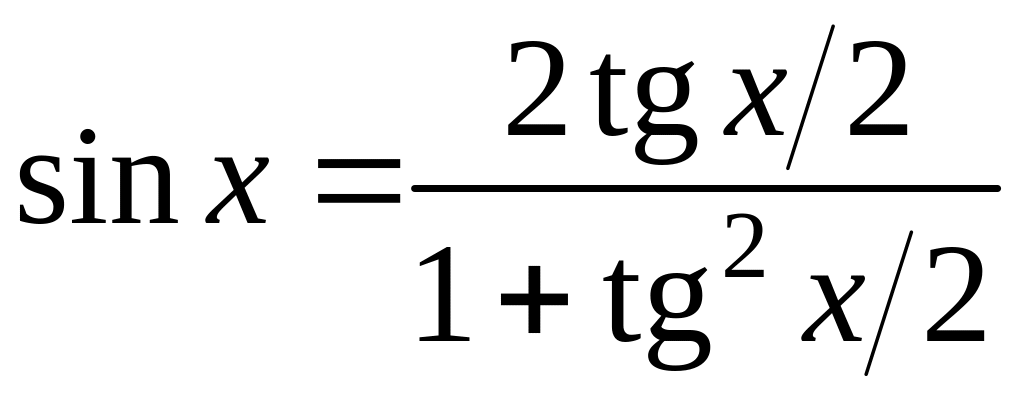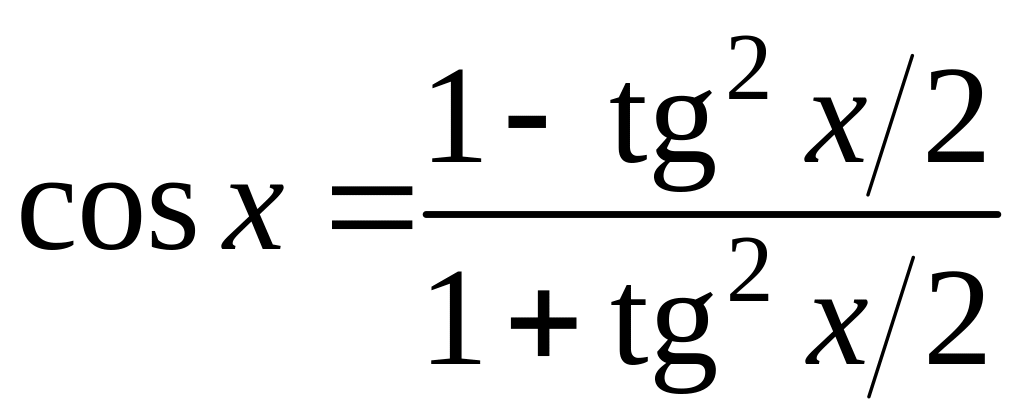