Завдання 1

Побудувати інтегральну суму для функції на проміжку і, користуючись означенням визначеного інтеграла, знайти .

.	.
.	.
.	.
.
.	.

10. . Поділити на рівні частини і вибрати лівим кінцем .

11. . Поділити на рівні частини і вибрати правим кінцем .

12. . Поділити на рівні частини і вибрати серединою проміжка .

13. . Поділити точками, які утворюють геометричну прогресію і вибрати правим кінцем .

14. . Поділити точками, які утворюють геометричну прогресію і вибрати лівим кінцем .

15. . Поділити точками, які утворюють геометричну прогресію і вибрати серединою проміжка .

В 1. (інтегрування нерівностей)

1) Якщо і для , тоді

;

2) Якщо і , тоді .

В 2. (Груба оцінка інтеграла). Якщо і

тоді .

В 3. (Теорема про середнє) Якщо , і для , тоді .

Наслідок: при число називають середнім значенням функції на .

Нехай , тоді функцію , де називають визначеним інтегралом з змінною верхньою границею інтегрування.

Теорема 1. Якщо , тоді і

1. (рівномірно неперервна на );

2. .

В 4. (Формула Лейбніца) Якщо і для , тоді

.

Приклад 2. Не обчислюючи, вказати який з інтегралів більший

і .

■ Оскільки для функція , тоді згідно В1 перший інтеграл менший від другого. ■

Приклад 3. Оцінити інтеграл .

■ При функції і монотонно спадні, отже і їх добуток є монотонно спадною функцією. Оскільки обидві функції неперервні на вказаному проміжку то, згідно з другою теоремою Weierstrass’а про неперервні функції на сегменті, функція набуває найбільшого і найменшого значень на кінцях сегмента: , , причому . Отже, згідно з В2

. ■

Приклад 4. Знайти точки екстремума функції при .

■ Функція є неперервною для , тоді згідно з теоремою 1

.

При . Знайдемо 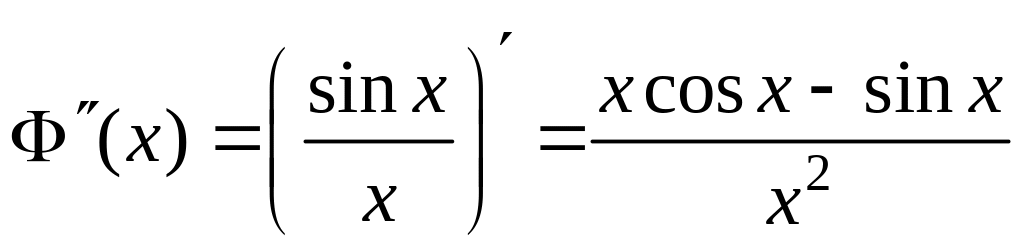. Тоді

Отже, при п – парному: , а при п – непарному: . Таким чином точки є точками мінімума функції , а точки є точками максимума функції .■

Приклад 5. Знайти .

■ При отримуємо невизначеність . Застосуємо правило L’Hospital’я (умови теореми виконуються) і В4:

. ■

Завдання 2

Не обчислюючи, вказати який з інтегралів більший

.	.
.	.

Використовуючи грубу оцінку інтеграла, оцінити наступні інтеграли

.	.	.
.	.	.
.

Знайти , якщо

.

Знайти для функції , яку задано параметрично

.	.
.

Знайти для функції , яку задано неявно

.

.

20. Знайти .

Знайти точки екстремума наступних функцій

.	.
.