Формула Ньютона–Лейбніца (основна теорема інтегрального числення).

1. Якщо функція і первісна функції на або

2. якщо функція і існує первісна на крім скінченого числа точок розриву першого роду, тоді справедлива формула

(1)

Теорема 2 (заміна змінної). Якщо

1. ;

2. ;

3. ;

4. строго монотонна на (нехай строго зростає). Тоді

(2)

Теорема 3 (інтегрування частинами). Якщо , тоді

. (3)

В 5. (Інтегрування парної і непарної функцій в симетричних границях)

1. , тоді ;

2. , тоді .

В 6. (Інтегрування періодичної функції по періоду)

Якщо , тоді не залежить від вибору точки .

В 7. Для

В 8. Для

Приклад 6. Знайти , де .

■ є інтегральною сумою функції на . Дійсно, побудуємо поділ поділивши на рівних частин. Тоді і виберемо . Функція і . Оскільки ( ), то справедлива формула (1) і

. ■

Завдання 3

Знайти , вказавши функцію , для якої є інтегральною сумою при певному виборі поділу і застосувавши формулу Ньютона–Лейбніца (1).

20. .

21. .

22. .

23. .

24. .

Знайти середнє значення функції на (див. В3).

.	.
.	.

Використовуючи теорему про середнє (В3), оцінити інтеграли

.	.		.
.	.		.
.		.

Застосувавши формулу Ньютона–Лейбніца, обчислити наступні інтеграли

.	.		.
.		.		.

Приклад 7. Обчислити інтеграли а) ; б) ;

в) .

■ а) Застосуємо заміну змінної (універсальна підстановка) , можливість якої справедлива оскільки функція монотонна на проміжку інтегрування. Тоді

, , .

	0
	0	1

Змінимо границі інтегрування

Отже

. ■

■ б) Вираз є диференціальним біномом: . Заміна раціоналізує невизначений інтеграл. Отримуємо і . Поміняємо границі інтегрування: , тоді , при , . Зауважимо, що функція монотонна при . Таким чином .■

791. ■ в) Проінтегруємо частинами: . Тоді

.

Обчислимо , інтегруючи частинами: , тоді

.

Отже, або . Отримуємо .■

Завдання 4

Обчислити наступні інтеграли, використовуючи заміну змінної

.	.	.
.	.	.
.	.	.
.	.	.
.	.	.

Обчислити інтеграли, використовуючи інтегрування частинами

.	.	.	.
.	.	.	.
.	.

Використовуючи В5 визначеного інтеграла, обчислити

.	.
.	.
.	.
.	.

Довести наступні рівності

.	.
,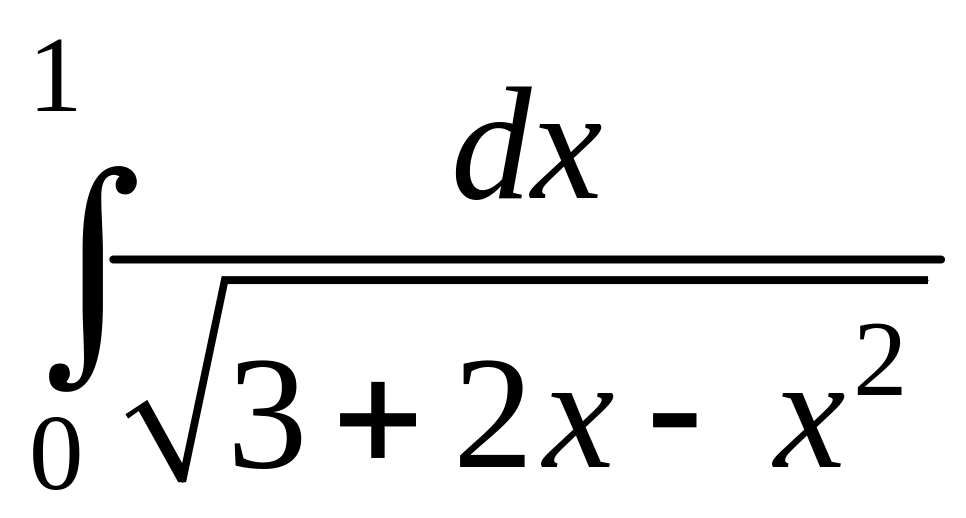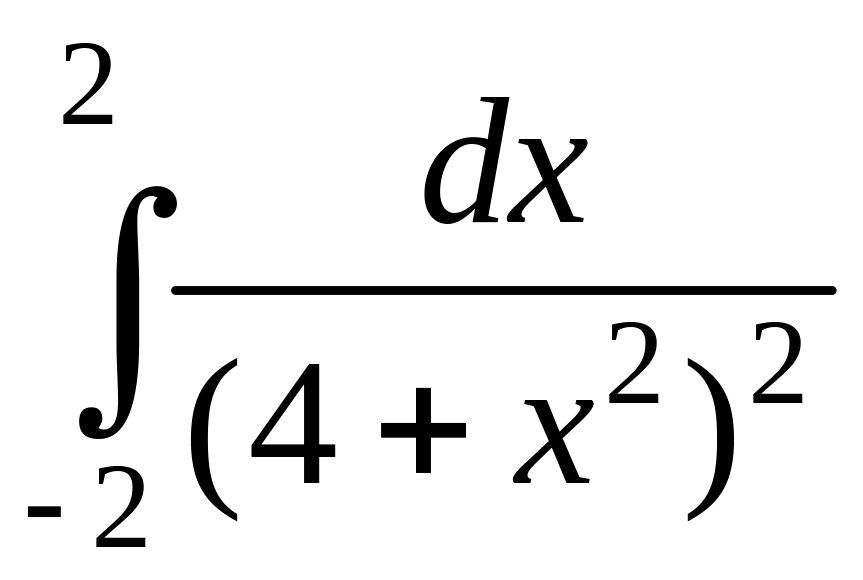