
- •Поліном Лагранжа
- •Завдання для самостійної роботи
- •Тема: Апроксимація функцій Теоретичні відомості Емпіричні формули
- •Визначення параметрів емпіричної залежності
- •Метод найменших квадратів
- •Розв’язок
- •Завдання для самостійної роботи
- •Розв’язок
- •Метод Сімпсона
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №3
- •Теоретичні відомості Чисельне розв’язання систем лінійних алгебраїчних рівнянь
- •Метод Гаусса
- •Метод Гаусса-Зейделя
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №4 Тема: Нелінійні рівняння Теоретичні відомості
- •Метод хорд
- •Метод Ньютона (метод дотичних)
- •Розв’язок
- •Комбінований метод хорд і дотичних
- •Метод ітерацій або метод послідовних наближень
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №5 Тема: Чисельне розв’язання звичайних диференційних рівнянь Теоретичні відомості
- •Метод Ейлера
- •Модифікації методу Ейлера
- •Метод Рунге-Кутта
- •Завдання для самостійної роботи
- •Список літератури
Метод Гаусса-Зейделя
Одним з найпоширеніших ітераційних методів, який відрізняється простотою і легкістю програмування, є метод Гаусса-Зейделя.
Проілюструємо спочатку цей метод на прикладі розв’язання системи:
|
(8) |
Припустимо,
що діагональні елементи
![]() відмінні від нуля (інакше можна переставити
рівняння).
відмінні від нуля (інакше можна переставити
рівняння).
Виразимо
невідомі
![]() відповідно з першого, другого і третього
рівнянь системи (8):
відповідно з першого, другого і третього
рівнянь системи (8):
|
(9) |
|
(10) |
|
(11) |
Задамо деякі
початкові (нульові) наближення значень
невідомих:
![]() ,
,
![]() :
:
|
Використовуючи
це значення для
![]() і наближення
і наближення
![]() для
для
![]() знаходимо з (10) перше наближення для
знаходимо з (10) перше наближення для
![]() :
:
|
І нарешті,
використовуючи обчислені значення
![]() ,
,
![]() ,
за допомогою виразу (11) обчислимо перше
наближення для
:
,
за допомогою виразу (11) обчислимо перше
наближення для
:
|
На цьому закінчується перша ітерація розв’язання системи (9) – (11).
Використовуючи
тепер значення
![]() можна таким чином провести другу
ітерацію, в результаті якої будуть
знайдені другі наближення до розв’язку
можна таким чином провести другу
ітерацію, в результаті якої будуть
знайдені другі наближення до розв’язку
![]() ,
,
![]() .
.
Наближення з
номером
можна обчислити, знаючи наближення з
номером
![]() ,
наступним чином:
,
наступним чином:
|
Ітераційний
процес продовжується до тих пір, доки
значення
![]() не стануть близькими із заданою похибкою
до значень
не стануть близькими із заданою похибкою
до значень
![]() .
.
Приклад.
Розв’язати за допомогою методу Гаусса-Зейделя наступну систему рівнянь:
|
Легко
перевірити, що розв’язок даної системи
наступний:
![]() .
.
Розв’язок
Виразимо невідомі відповідно з першого, другого і третього рівнянь:
|
У якості початкового
наближення (як це зазвичай робиться)
приймемо
![]()
![]() :
:
|
Аналогічно обчислимо наступні наближення:
|
Ітераційний процес можна продовжувати до отримання малої різниці між значеннями невідомих в двох послідовних ітераціях.
Розглянемо тепер систему лінійних рівнянь з невідомими. Запишемо її у виді:
|
Тут також будемо припускати, що всі діагональні елементи відрізняються від нуля. Тоді відповідно до методу Гаусса-Зейделя -е наближення до розв’язку можна представити у виді:
|
(12) |
Ітераційний
процес продовжується до тих пір, доки
всі значення
![]() не стануть близькими до
не стануть близькими до
![]() .
Як критерій завершення ітерацій
використовується одна з умов (13) – (15).
.
Як критерій завершення ітерацій
використовується одна з умов (13) – (15).
Якщо
задана допустима похибка
![]() ,
то критерієм закінчення
ітераційного процесу можна вважати
одну з трьох нерівностей:
,
то критерієм закінчення
ітераційного процесу можна вважати
одну з трьох нерівностей:
|
(13) |
|
(14) |
|
(15) |
Для збіжності ітераційного процесу (12) достатньо, щоб абсолютні величини діагональних коефіцієнтів для кожного рівняння системи були не менші сум модулів всіх інших коефіцієнтів:
|
(16) |
При цьому хоч би для одного рівняння нерівність повинна виконуватися строго. Ці умови є достатніми для збіжності методу, але вони не є необхідними, тобто для деяких систем ітерації сходяться і при порушенні умов (16).

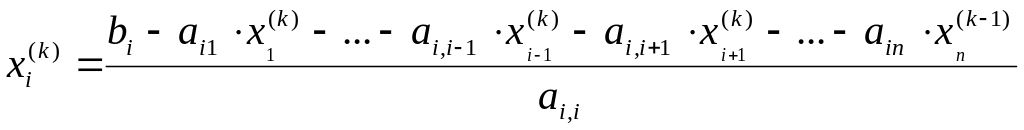 ,
(
,
(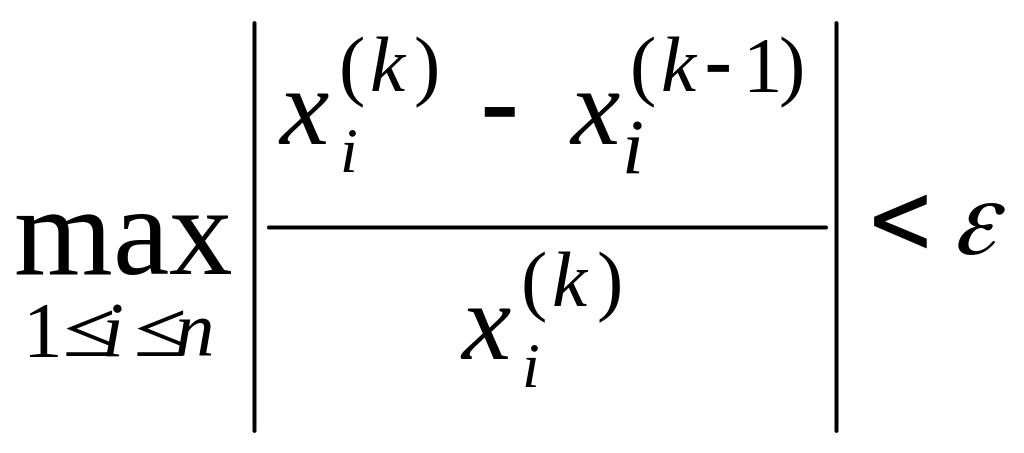 при
при