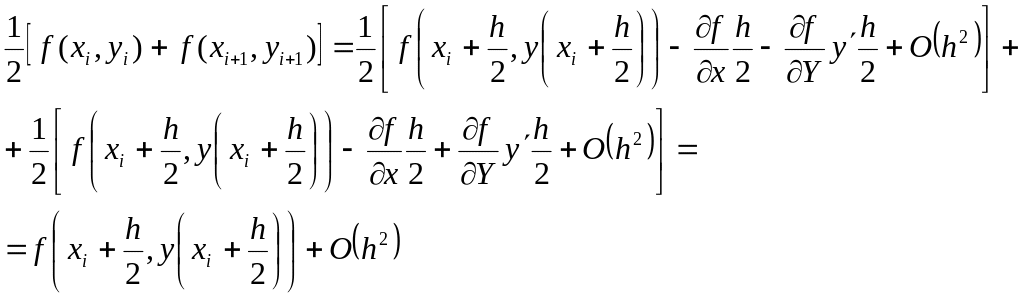- •Поліном Лагранжа
- •Завдання для самостійної роботи
- •Тема: Апроксимація функцій Теоретичні відомості Емпіричні формули
- •Визначення параметрів емпіричної залежності
- •Метод найменших квадратів
- •Розв’язок
- •Завдання для самостійної роботи
- •Розв’язок
- •Метод Сімпсона
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №3
- •Теоретичні відомості Чисельне розв’язання систем лінійних алгебраїчних рівнянь
- •Метод Гаусса
- •Метод Гаусса-Зейделя
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №4 Тема: Нелінійні рівняння Теоретичні відомості
- •Метод хорд
- •Метод Ньютона (метод дотичних)
- •Розв’язок
- •Комбінований метод хорд і дотичних
- •Метод ітерацій або метод послідовних наближень
- •Розв’язок
- •Завдання для самостійної роботи
- •Лабораторна рОбота №5 Тема: Чисельне розв’язання звичайних диференційних рівнянь Теоретичні відомості
- •Метод Ейлера
- •Модифікації методу Ейлера
- •Метод Рунге-Кутта
- •Завдання для самостійної роботи
- •Список літератури
Метод Ейлера
Нехай задано звичайне диференційне рівняння першого порядку:
|
(4) |
Необхідно знайти
розв’язок цього рівняння
![]() ,
який задовольняє початковій умові:
,
який задовольняє початковій умові:
|
(5) |
Така задача називається задачею Коші.
Чисельний
розв’язок задачі Коші полягає в
знаходженні значень
![]() у точках
у точках
![]() ;
;
![]() ;
…;
;
…;![]() відрізка
відрізка
![]() ,
де h–крок
інтегрування;
,
де h–крок
інтегрування;
![]() ;
;
![]() .
.
Розглянемо рівняння
(4) в околі вузлів
![]() (
(![]() )
та замінимо у лівій частині похідну
)
та замінимо у лівій частині похідну
![]() правою різницею (
правою різницею (![]() ,
,
![]() ,
,
![]() ). При цьому значення функції
у вузлах
). При цьому значення функції
у вузлах
![]() замінимо значеннями сіткової функції
замінимо значеннями сіткової функції
![]() :
:
|
(6) |
Отримана
апроксимація диференційного рівняння
(4) має перший порядок, так як заміняючи
(4) на (6) допускається похибка
![]() .
.
Припустимо, що
вузли рівновіддалені, тобто
![]() (
).
Тоді із рівності (6) отримаємо:
(
).
Тоді із рівності (6) отримаємо:
|
(7) |
Зауважимо, що з рівняння (4) випливає наступне:
|
Тому
(7) представляє собою наближене знаходження
значення функції
у точці
![]() за допомогою розкладання у ряд Тейлора.
Іншими словами, приріст функції
припускається рівним її диференціалу.
за допомогою розкладання у ряд Тейлора.
Іншими словами, приріст функції
припускається рівним її диференціалу.
Припускаючи
![]() ,
за допомогою співвідношення (7), знаходимо
значення сіткової функції
,
за допомогою співвідношення (7), знаходимо
значення сіткової функції
![]() при
при
![]() :
:
|
Необхідне
тут значення
![]() задано початковою умовою (5).
задано початковою умовою (5).
Аналогічно можна знайти значення сіткової функції у інших вузлах:
|
Цей
алгоритм називається методом
Ейлера.
Різницева схема цього методу представлена
співвідношенням (7). Вона має вид
рекурентних формул, за допомогою яких
значення сіткової функції
![]() у будь-якому вузлі
обчислюється по її значенню
у попередньому вузлі
.
У зв’язку з цим метод Ейлера відноситься
до однокрокових методів.
у будь-якому вузлі
обчислюється по її значенню
у попередньому вузлі
.
У зв’язку з цим метод Ейлера відноситься
до однокрокових методів.
Метод Ейлера найпростіший і порівняно грубіший чисельний метод інтегрування.
Приклад.
Розв’язати
диференційне рівняння
![]() в інтервалі
в інтервалі
![]() ,
,
![]() .
.
Розв'язок
|
Нехай
![]() .
Розв'язок задачі представимо в вигляді
таблиці 1.
.
Розв'язок задачі представимо в вигляді
таблиці 1.
Таблиця 1
i |
xi |
yi |
F(xi,yi) |
0 |
0 |
0 |
|
1 |
1 |
0,05 |
|
2 |
2 |
|
|
3 |
3 |
|
|
4 |
4 |
|
|
5 |
5 |
|
|
6 |
6 |
|
|
7 |
7 |
|
|
8 |
8 |
|
|
9 |
9 |
|
|
10 |
10 |
|
|
Таким
чином,
![]() .
.
Модифікації методу Ейлера
Розглянемо рівняння
(4) в околі вузлів
![]() (
(![]() ),
які є серединами відрізків [
),
які є серединами відрізків [![]() ].
У лівій частині (4) замінимо похідну
центральною різницею (
].
У лівій частині (4) замінимо похідну
центральною різницею (![]() ,
,
![]() ,
,
![]() ),
а в правій частині замінимо значення
функції
),
а в правій частині замінимо значення
функції
![]() середньоарифметичним значенням функції
середньоарифметичним значенням функції
![]() у точках (
у точках (![]() )
і (
)
і (![]() ).
Тоді замість (6) запишемо:
).
Тоді замість (6) запишемо:
|
(8) |
Звідси:
|
(9) |
Отримана
схема є неявною, оскільки шукане значення
![]() входить в обидві частини співвідношення
(9) і його, взагалі кажучи, не можна
виразити явно. Для обчислення
можна застосувати один з ітераційних
методів. Якщо є хороше початкове
наближення
входить в обидві частини співвідношення
(9) і його, взагалі кажучи, не можна
виразити явно. Для обчислення
можна застосувати один з ітераційних
методів. Якщо є хороше початкове
наближення
![]() ,
то можна побудувати рішення з використанням
двох ітерацій наступним чином. Вважаючи
початковим наближенням, обчислюється
перше наближення
,
то можна побудувати рішення з використанням
двох ітерацій наступним чином. Вважаючи
початковим наближенням, обчислюється
перше наближення
![]() по формулі методу Ейлера (7):
по формулі методу Ейлера (7):
|
(10) |
Обчислене значення підставляємо замість у праву частину співвідношення (9) і знаходимо остаточне значення:
|
(11) |
Алгоритм (10), (11) можна записати у виді одного співвідношення:
|
Дані рекурентні
співвідношення описують нову різницеву
схему, що є модифікацією методу Ейлера,
яка називається методом Ейлера з
перерахунком. Покажемо, що цей метод
відрізняється від методу Ейлера більшою
точністю. Апроксимація (8) має, на відміну
від (6), другий порядок. Дійсно, при заміні
похідною в лівій частині (4) допускається
похибка
![]() .
Похибка такого ж порядку має місце і
при заміні правої частини (4) правою
частиною (8):
.
Похибка такого ж порядку має місце і
при заміні правої частини (4) правою
частиною (8):
|
Тут
проведено розклад функції
у ряд в околі крапки
![]() .
.
Похибка, що
допускається при обчисленні
по формулі (9), складає
![]() .
Цей порядок похибки зберігається і при
використанні двох ітерацій (10), (11),
оскільки:
.
Цей порядок похибки зберігається і при
використанні двох ітерацій (10), (11),
оскільки:
|
Таким
чином, похибка на кожному кроці (локальна)
має порядок
![]() ,
а сумарна по аналогії з (7) –
,
а сумарна по аналогії з (7) –
![]() на відміну від
на відміну від
![]() у звичайному методі Ейлера. Тобто метод
Ейлера з перерахунком має другий порядок
точності.
у звичайному методі Ейлера. Тобто метод
Ейлера з перерахунком має другий порядок
точності.
Відмітимо, що при використанні неявної схеми (9) виходить практично те ж значення , що і в методі Ейлера з перерахунком. Проте застосування схеми (9), що вимагає побудови ітераційного процесу для обчислення значення привело б до значного зростання часу розрахунку на кожному кроці.
На рис. 1
зображено геометричну інтерпретацію
першого кроку при розв’язанні задачі
Коші методом Ейлера з перерахунком.
Дотична до кривої
![]() у точці
у точці
![]() проводиться з кутовим коефіцієнтом
проводиться з кутовим коефіцієнтом
![]() .
З її допомогою за методом Ейлера (7)
знайдено значення
.
З її допомогою за методом Ейлера (7)
знайдено значення
![]() ,
яке використовується для визначення
нахилу дотичної
,
яке використовується для визначення
нахилу дотичної
![]() у точці
у точці
![]() .
Відрізок з таким нахилом замінює
первинний відрізок дотичної від точки
.
Відрізок з таким нахилом замінює
первинний відрізок дотичної від точки
![]() до точки
.
В результаті виходить уточнене значення
шуканої функції
у цій точці.
до точки
.
В результаті виходить уточнене значення
шуканої функції
у цій точці.
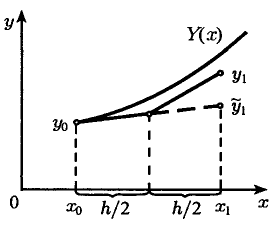
Рисунок 1 – Метод Ейлера з перерахунком
За
допомогою методу Ейлера з перерахунком
можна проводити контроль точності
рішення шляхом порівняння значень
![]() і
і
![]() і вибору на підставі цього відповідної
величини кроку
у кожному вузлі. А саме, якщо величина
і вибору на підставі цього відповідної
величини кроку
у кожному вузлі. А саме, якщо величина
![]() порівнянна з похибками обчислень, то
крок потрібно збільшити; інакше, якщо
ця різниця дуже велика (наприклад
порівнянна з похибками обчислень, то
крок потрібно збільшити; інакше, якщо
ця різниця дуже велика (наприклад
![]() ),
значення
слід зменшити. Використовуючи ці оцінки,
можна побудувати алгоритм методу Ейлера
з перерахунком з автоматичним вибором
кроку.
),
значення
слід зменшити. Використовуючи ці оцінки,
можна побудувати алгоритм методу Ейлера
з перерахунком з автоматичним вибором
кроку.
Разом з методом Ейлера з перерахунком використовується і інша модифікація методу Ейлера. Так само, як і в методі Ейлера з перерахунком, розглянемо рівняння (4) в околі вузлів ( ). В лівій частині (4) замінимо похідну центральною різницею ( , , ), а праву частину залишимо без змін:
|
(12) |
Наближене
значення функції
у точці
![]() обчислимо за допомогою методу Ейлера:
обчислимо за допомогою методу Ейлера:
|
(13) |
Виразимо
з (12), замінивши
![]() його наближенням
його наближенням
![]() :
:
|
(14) |
Отриманий метод у виді формул (13), (14) називається вдосконаленим методом Ейлера. Неважко показати, що він також має другий порядок точності.

 .
.