Розв’язок

За умовою . Визначаємо другу похідну :

.

Таким чином , тому .

Визначаємо значення першої похідної в точці :

.

Для зручності подальші обчислення зводимо в таблицю 2.

Таблиця 2

0	-2,75	-20,797	7,5625	22,6875	-1,111	0,179
1	-2,571	-16,994	6,6100	19,8300	-0,164	0,026
2	-2,545	-16,484	6,4770	19,431	-0,053	0,008
3	-2,537	-16,329	6,4364	19,309	0,020	0,003
4	-2,534	-16,271	6,4212	19,2636	0,007	0,001
5	-2,533

Остаточно одержимо .

Комбінований метод хорд і дотичних

Методи хорд і дотичних дають наближення кореня з різних сторін (більше або менше дійсного значення кореня), тому їх часто застосовують в поєднанні один з одним, і уточнення кореня відбувається швидше.

Якщо , то метод хорд дає наближення кореня з недостачею, а метод дотичних – з надлишком. Якщо ж , то методом хорд набуває значення кореня з надлишком, а методом дотичних – з недостачею.

Проте у всіх випадках дійсне значення кореня розташоване на проміжку між наближеними значеннями коріння, що утворюється за методом хорд і методом дотичних.

Нехай і ‑ наближені значення кореня з недостачею і з надлишком відповідно.

1. Якщо на , то:

;

(12)

(при цьому );

2. Якщо на , то:

;

(13)

(при цьому ).

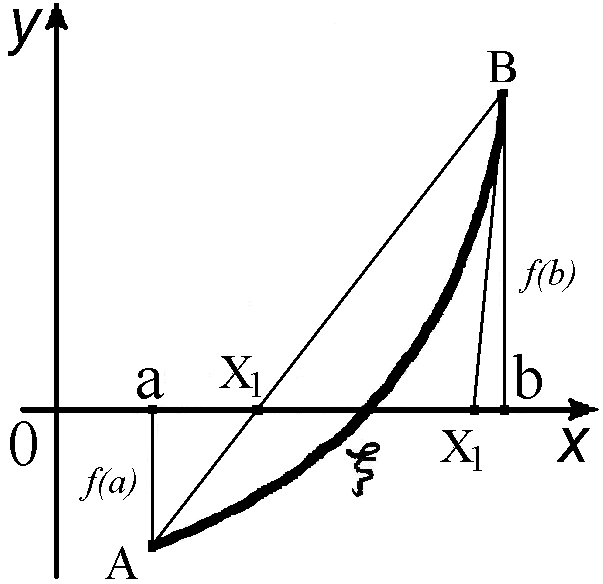
Рисунок 4 – Ілюстрація комбінованого методу хорд і дотичних

Процес обчислень припиняється, як тільки буде виконуватися нерівність:

.

Значення кореня, який є уточненим, буде становити:

.

Метод ітерацій або метод послідовних наближень

Для застосування методу ітерацій (латинське "ітераціо" ‑ повторення) початкове рівняння ( ‑ безперервна функція) необхідно, по-перше, записати у вигляді , по-друге, виділити інтервал ізоляції кореня цього рівняння, і по-третє, обрати нульове наближення кореня . Для одержання першого наближення в праву частину рівняння замість підставляємо , так що .

Наступні наближення утворюються за схемою:

.

(14)

Таким чином, у результаті застосування деякого однакового процесу будуються послідовні наближення .

При цьому можливі два випадки:

– процес може збігатися, тобто послідовні наближення прямують до деякої кінцевої межі , що є коренем рівняння;

– процес може розходитися, тобто кінцева межа побудованих наближень існувати не буде; з цього не випливає, що розв'язку початкового рівняння не існує, просто процес послідовних наближень міг бути обраний невдало.

Збіжність процесу ітерації визначається наступною теоремою.

Теорема. Нехай інтервал є інтервалом кореня рівняння , а функція визначена і диференційована на всьому інтервалі, причому всі її значення .

Тоді, якщо існує правильний дріб такий, що , то:

1. Процес ітерації є збіжним незалежно від початкового значення ;

2. Граничне значення є єдиним коренем рівняння на відрізку .

Наближення слід обчислювати доти, поки не буде виконано нерівність:

,

де ‑ задана гранична абсолютна похибка кореня .

Якщо і додатня навколо кореня, то послідовні наближення і сходяться до кореня монотонно. Якщо ж похідна від'ємна, то послідовні наближення коливаються біля кореня .

Приклад.

Методом ітерацій уточнити з точністю корінь рівняння , який ізольований на відрізку [0, 1].