Вероятности ошибок

Под ошибкой первого рода понимается ложная тревога. Вероятность ошибки первого рода вычисляется как:

- для непрерывной случайной величины ;

- для дискретной случайной величины .

Под ошибкой второго рода понимается пропуск цели. Вероятность ошибки второго рода вычисляется как:

- для непрерывной случайной величины ;

- для дискретной случайной величины .

Вероятность – носит название вероятности правильного обнаружения.

Как правило, наблюдения распределены по нормальному закону:

На рисунке ниже показаны ошибки первого и второго рода для случая нормального распределения наблюдений.

Обычно, в задачах обнаружения пропуск цели штрафуется дороже, чем ложная тревога. Для значений функции потерь, приведенных в таблице, , .

Таблица 1

С(x,d)	d=d1	d=d0
x=x1	c11	c10
x=x0	c01	c00

Рабочая характеристика решающего правила

На рисунке ниже показаны характеристики , и семейства решающих правил . Характеристика показывает зависимость вероятности правильного обнаружения объекта и вероятности ложной тревоги. Для приведенных характеристик справедливо следующее соотношение: . В качестве примера характеристики решающего правила можно рассмотрим отношение сигнал/шум. Тогда, в случае нормального распределения наблюдений и при условии, что , .

– функция мощности решающего правила. Под мощностью решающего правила при заданном значении понимают вероятность принятия правильного решения при заданном состоянии среды.

Байесово решающее правило

Условные риски от принятия решающего правила равны (здесь и далее используются значения функции потерь из таблицы 1):

;

.

Средний риск принятия решающего правила равен:

.

Апостериорный риск принятия решающего правила равен:

;

.

Байесовское решающее правило :

.

Рассмотрим случай, когда , тогда .

Выполним ряд преобразований:

;

.

С учетом того, что , получаем:

.

Тогда ,

где – отношение правдоподобия;

– пороговое значение.

При равных вероятностях обычно и тогда .

Пример. Пусть задана функция правдоподобия , вероятности нахождения пространства в различных состояниях одинаковые , пороговое значение . На рисунке ниже показана функция правдоподобия и граница разбиения множества наблюдений .

Отношение правдоподобия показано на рис. ниже

Если наблюдения имеют нормальное распределение, т.е.

;

, тогда отношение правдоподобия имеет вид:

.

Для удобства используется логарифм отношения правдоподобия:

.

Тогда байесовское решающее правило имеет вид:

.

Максимум апостериорной вероятности

Функция потерь , где . Тогда , и пороговое значение .

Условный риск равен:

;

.

Средний риск равен:

.

Минимизируем вероятность принятия неправильного решения

Максимум правдоподобия

При пороговое значение .

Средний риск равен: .

Решающее правило Неймана-Пирсона

Решающее правило Неймана-Пирсона представляет собой семейство решающих правил и является пороговым:

,

где определяется из условия:

,

где α – заданная вероятность ложной тревоги.

Решающее правило Неймана-Пирсона принято характеризовать с использованием функции мощности решающего правила .

Лемма Неймана-Пирсона

Решающее правило Неймана-Пирсона для любого значения вероятности ложной тревоги и для любого решающего правила обладает наиболее мощным среди всех решающих правил:

, или

, .

Следствие: Решающее правило Неймана-Пирсона является допустимым при простой функции потерь:

- допустимое решающее правило.

Доказательство:

;

и если

, то

.

Доказательство (леммы):

Пусть - пространство наблюдений, – область пространства наблюдений, при попадании наблюдения в которую решающее правило Неймана-Пирсона принимает значение , – область пространства наблюдений, при попадании наблюдения в которую произвольное решающее правило принимает значение .

Введем ряд обозначений (см. рисунок ниже):

;

;

.

= =

При переходе (1) использовалось соотношение: , . При переходе (2) учитывалось, что , т.к. - порог для , а =Ø.

Замечание. При выполняется строгое равенство .

Структура решающих правил

Все решающие правила можно рассматривать как правила Неймана-Пирсона при фиксированном с помощью порога значении , а это значит, что и МАВ и МП и байесовские решающие правила дают допустимую решающую функцию. В тоже время все критерии можно рассматривать как байесовские при постой функции потерь. В таблице ниже приведены решающие правила и соответствующие им пороги.

Решающее правило	Порог
Байесово решающее правило
МАВ (максимум апостериорной вероятности)
МП (максимум правдоподобия)	1
Н-П (решающее правило Неймана-Пирсона)	Определяется з условия

Рассмотрим задачу обнаружения самолета радиолокационными средствами. На рисунке ниже показаны функции правдоподобия для состояний среды и при наличии наблюдений . При отражении сигнала от самолета сигнал хорошо локализован и имеет меньшую дисперсию, при отражении от облаков сигнал плохо локализован.

На рисунках ниже показано множество решающих правил и решающие правила для МП, байесова решающего правила и решающего правила Неймана-Пирсона.

Решающее правило МП есть точка касания границы множества и прямой, проведенной под углом 135° к оси абсцисс.

Байесово решающее правило есть точка касания границы множества и прямой, проходящей через точку .

Решающее правило Неймана-Пирсона определяется соответствующими значениями и .

d0

Множество точек обладает свойством поворотной симметрии относительно прямой , , т.е. симметрией относительно вращения на 180°. Симметричность области следует из возможности для любого разбиения , построить разбиение , , тогда

;

.

Асимметрия области относительно биссектрисы объясняется различием функций правдоподобия и .

Последовательные решения

До сих пор рассматривалась задача принятия решения на основе анализа всех имеющихся измерений (наблюдений). Однако, если вектор наблюдения можно рассматривать как последовательность векторов , каждый из которых получен в момент времени имеет смысл рассматривать задачу принятия решения как совокупность двух задач:

а) принятие решения об остановке наблюдений;

б) принятия решения по имеющимся к моменту остановки наблюдения измерениям.

Рассмотрим простую двухальтернативную задач. Пусть покупателю нужно принять решение о закупке партии товара, например, лампочек на основе закупки и исследования пробной партии. Множество состояний партии лампочек , где - партия лампочек не является бракованной, - партия лампочек бракованная. Множество решений , где - решение о закупке партии лампочек, - решение об отказе о закупке партии лампочек. Множество измерений на момент времени будем обозначать , . Пусть измерения являются независимыми: . Требуется определить момент , после которого наблюдения дальше не производятся и по совокупности измерений принять решение или .

Рассмотрим разбиение пространства , где - область продолжения наблюдений, - область принятия решения , - область принятия решения . При этом Ø, .

В качестве критерия оптимальности будем использовать среднее количество измерений , необходимое для принятия решения при заданных вероятностях ошибок I и II рода.

Для принятия решения будем использовать отношение правдоподобия , или его логарифм , .

Математик А. Вальд (1947 г.) показал, что при заданных ошибках первого рода и второго рода наименьшим временем анализа обладает процедура вида:

,

где и - некоторые пороговые значения.

На рисунке ниже показаны пороги и на пря мой .

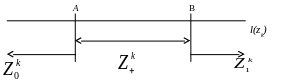
Покажем, что для порогов и справедливы следующие соотношения:

, .

Действительно, , где при переходе (1) учтено, что , .

Аналогично: , где при переходе (1) учтено, что, , .

На рисунке ниже показаны пороги и на пря мой с учетом полученных соотношений.

Замечание. Для того чтобы обеспечить выполнение неравенства достаточно, что бы , . Действительно, , тогда . Из получено неравенства следует, что и .

Точные значения порогов вычислить трудно, поэтому полагают, что: , . Тогда решения становятся более осторожными и увеличивается среднее время до принятия решения, т.е. в рассматриваемом примере увеличивается количество лампочек, которые нужно проверить до принятия решения.

При изменении пороговых значений вероятности ошибок I и II рода также изменятся: , . Для новых значений вероятностей выполняются следующие соотношения: , откуда .

Сложив неравенства, получаем:

;

,

откуда .

Примечание. На практике обычно работают с логарифмом отношения правдоподобия . Тогда

;

;

.

При работе с логарифмом отношения правдоподобия для нормального закона не требуется вычислять экспоненту.

На рисунке ниже показаны пороги и на пря мой .

Утверждение. Количество наблюдений до остановки наблюдений конечно, т.е. процедура последовательного анализа является конечной: , как при принятии решения , так и при принятии решения .

Лемма. Пусть – последовательность независимых одинаково распределенных случайных величин с математическим ожиданием случайных величин. Тогда для всякой последовательной процедуры со свойством имеет место равенство:

.

Оценка количества наблюдений

Пусть множество состояний природы , множество решений . Рассмотрим две гипотезы: , .

При состоянии природы получаем , где , где - номер последнего наблюдения, где , .

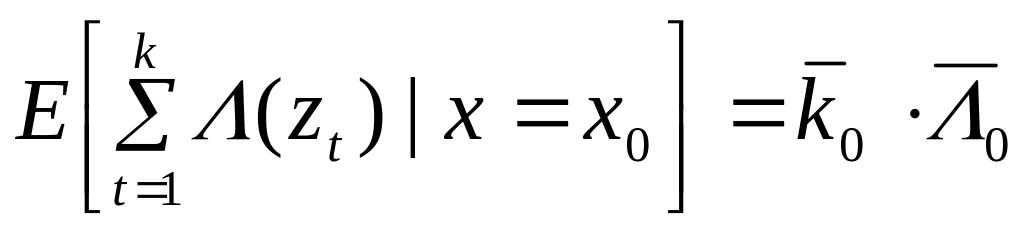При состоянии природы получаем , где , где - номер последнего наблюдения, где . .

В среднем для принятия решения необходимо выполнить измерений, для принятия решения необходимо в среднем измерений.

На рисунке ниже показаны функции апостериорной вероятности для состояний среды и при наличии наблюдения .

Значения , .

Если , тогда . Если , тогда 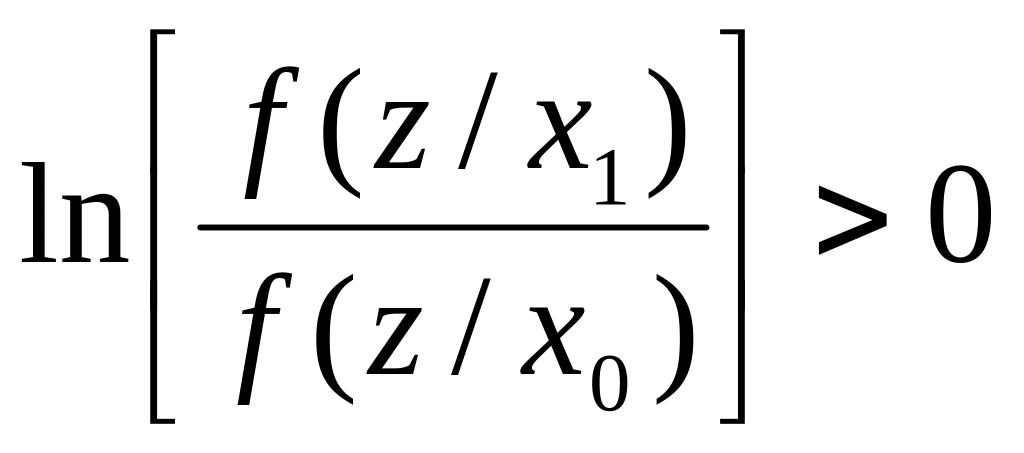, и принимается решение .

В общем виде для принятия некоторого решения необходимо в среднем выполнить измерений:

, .

Найдем числитель этого выражения. Для этого будем считать, что в момент остановки или .

Тогда вероятности событий равны:

Откуда

, тогда

, .

Усеченные процедуры

Последовательная процедура имеет минимальное среднее время анализа, однако некоторая реализация процедуры может оказаться непомерно длинной. Поэтому, обычно, заранее выбирают число , являющееся максимальным номером наблюдения, исходя из заданной вероятности . Если решение не принято последовательной процедурой, то оно принимается, например, по методу Неймана-Пирсона. При этом ухудшается качество решения, т.е. оказывается больше.

Пусть провели серию из наблюдений. В результате был получен вектор наблюдений . После наблюдений ресурс наблюдений оказался исчерпан. Применим классическую схему: вычислим отношение правдоподобия , решение , где ∆ – пороговое значение.

Усеченная пороговая процедура дает решения хуже по сравнению с классической процедурой, поскольку при принятии решения используется аномальная последовательность наблюдений.

Наблюдение в форме прогноза