Точечные оценки Фишберна (Fishburn)

Рассмотрим некоторые варианты возможной качественной информации о состоянии среды.

1. Пусть известно, что для вероятностей состояний окружающей среды справедливо следующее соотношение:

(*).

В качестве распределения вероятностей выбирается распределение, максимизирующее значение функционала . Поскольку на задано отношение порядка, то можно использовать функцию неопределенности II рода:

.

Вычислим максимум функции неопределенности:

.

Решением задачи оказывается , . Полученные оценки вероятностей носят название точечных оценок Фишберна.

Проверим, что .

.

Вычислим точечные оценки Фишберна для M=3:

; ; ;

для M=4 ; ; ; .

2. Пусть известно, что для вероятностей состояний окружающей среды справедливо следующее соотношение:

, (*).

При выполнении условия (*) можно считать оценки вероятностей равными: , взяв .

Тогда ; ,…, . В общем виде .

Найдем значение λ, из условия :

= ;

;

.

Тогда точечные оценки Фишберна равны: .

Вычислим точечные оценки Фишберна для M=5:

; ; ; ; .

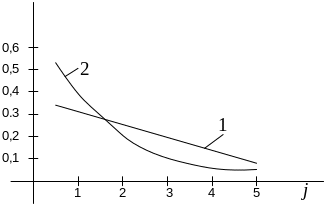
На графике показы значения точечных оценок Фишберна для обычного отношения порядка (1) и усиленного отношения порядка (2).

Дополнение к точечным оценкам Фишберна

Рассмотрим множество состояний природы , априорное распределение вероятностей . Тогда все возможные распределения образуют множество

.

Множество носит название -мерного симплекса.

На рисунке ниже показан симплекс для .

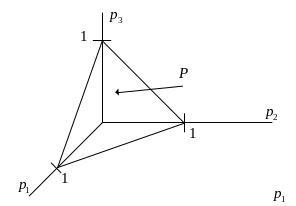
Уменьшим размерность задачи. Рассмотрим

; .

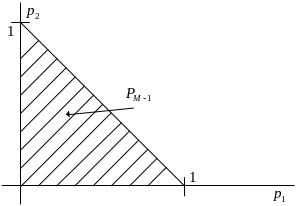
Множество носит название -мерного симплекса. Пример -мерного симплекса для (двумерный симплекс) показан на рисунке ниже. Двумерный симплекс – линейная (выпуклая) оболочка любых трех точек, не лежащих на одной прямой (треугольник).

Байесовым множеством решающего правила будем называть множество точек симплекса ( ), таких, что

; ;

, .

Точки, попадающие сразу в несколько множеств , относятся произвольно к одному из множеств, так чтобы , =Ø, .

Понятия байесова множества введено с целью анализа выявления ошибок в задании распределения на принимаемые решения.

Утверждение. Байесовы множества являются выпуклыми множествами.

Доказательство. Рассмотрим доказательство утверждения для . Линии равного уровня риска в пределах есть отрезки прямых:

, т.е. и связаны линейно, причем линии параллельны, т.к. коэффициенты , , не изменяются. Следовательно множество является выпуклым.

Пример. Пусть M=2, множество решающих правил и задана таблица рисков.

	5	3	2	3
	-1	3	4	1

Необходимо в зависимости от распределения состояний окружающей среды, определить байесов риск для каждого решающего правила . Поскольку распределение вероятностей не известно, то рассматриваем задачу как параметрическую по отношению к вероятности .

Рассмотрим байесовские множества:

;

Ø, поскольку решающее правило недопостимо, т.к. доминируется решающим правилом .

;

.

На рисунке ниже показаны байсовы множества и байесова поверхность .

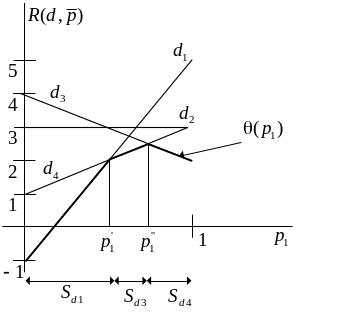
В общем виде байесова поверхность ,

где ;

.

Байесова поверхность образуется гиперплоскостями размерности .

Пример. Пусть M=3 и пусть задана таблица рисков

	0	2	4	5
	6	1	1	4
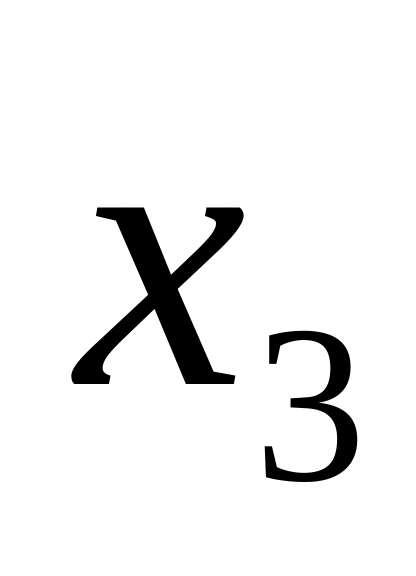
	4	4	3	2

Вычислим значение среднего риска для решающих правил :

;

;

;

;

Вычислим байесово множество .

Для этого найдем:

а) границу между множествами и :

б) границу между множествами и :

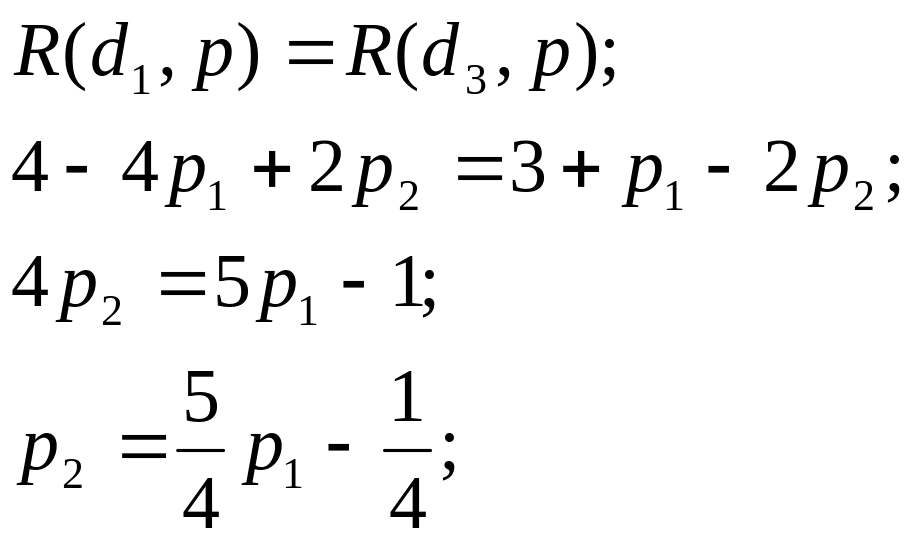
в) границу между множествами и :

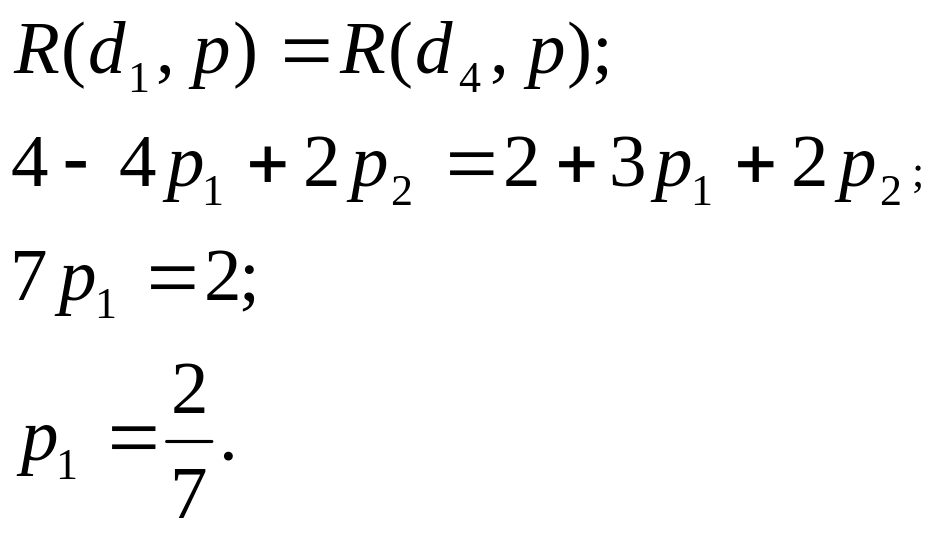
На рисунке ниже показано байесово множество .

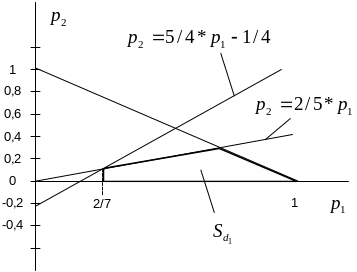
Вычислим байесово множество .

Для этого найдем:

а) границу между множествами и :

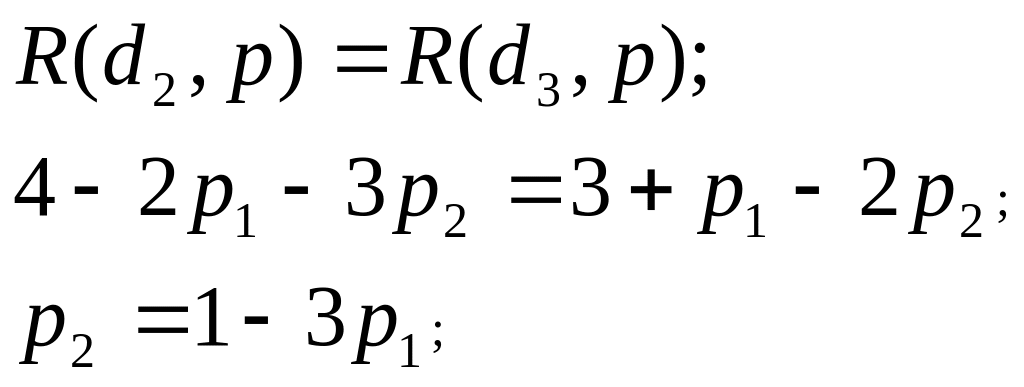
б) границу между множествами и :

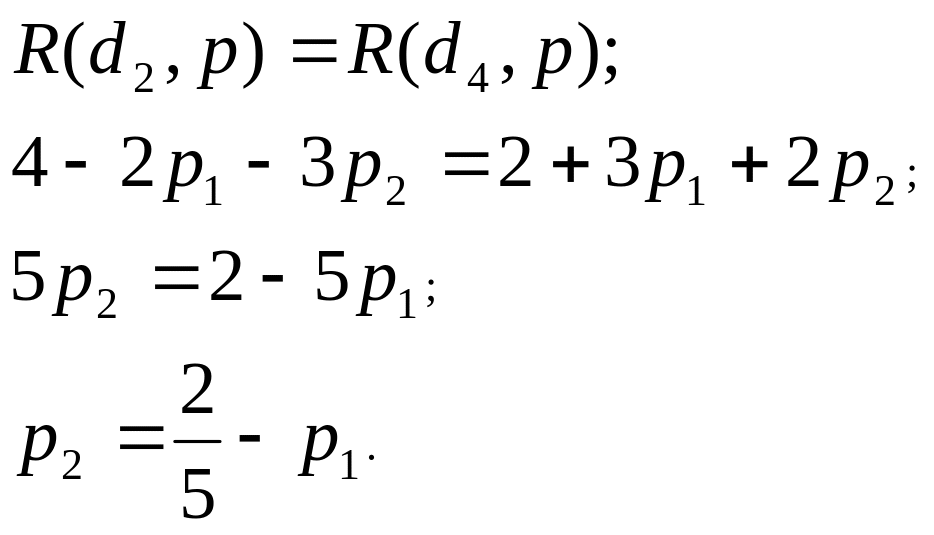
Вычислим байесово множество .

Для этого найдем:

а) границу между множествами и :

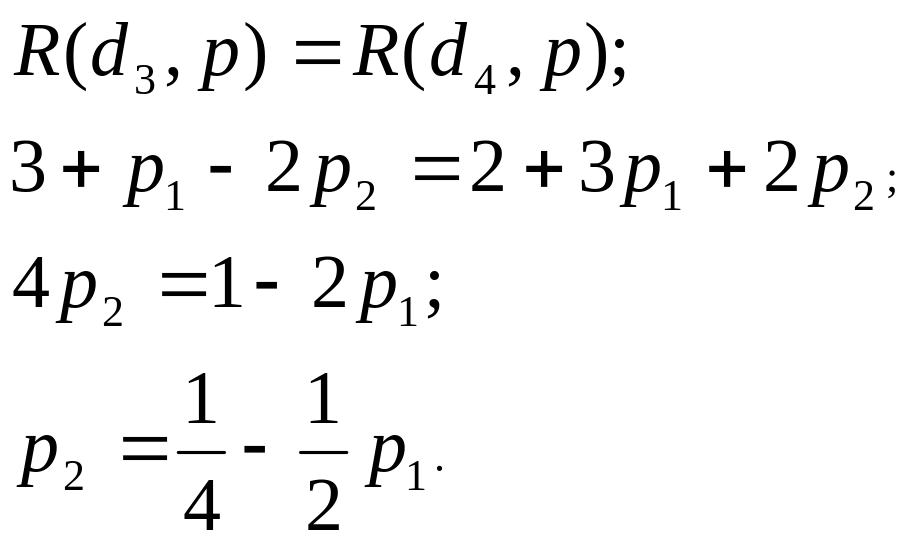
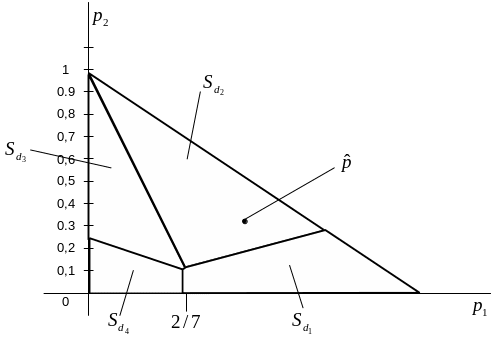
Точечные оценки Фишберна для M=3:

; ; .

Вычислим значение риска для решающих правил:

;

;

;

.

Для второго решающего правила риск минимален.

Чувствительность и устойчивость байесовских решающих правил