Допустимые решающие правила

Определение. Будем говорить, что решающее правило d’ доминирует решающее правило d’’, если для любого состояния среды X риск, связанный с применением правила d’ не превышает риск d’’, и, кроме того существует некоторое состояние окружающей среды, при котором неравенство становится строгим:

: ,

где .

Определение. Будем говорить, что решающее правило d’ доминирует решающее правило d’’, если для любого состояния среды X доход, связанный с применением правила d’ не меньше дохода d’’, и, кроме того существует некоторое состояние окружающей среды, при котором неравенство становится строгим:

: ,

где .

Определение. Решающее правило будем называть допустимым, если не существует решающее правило, которое бы его доминировало:

допустимо, если .

Пример. На рисунке ниже показаны три решающих функции , , , Решающая функция доминирует решающую функцию: .

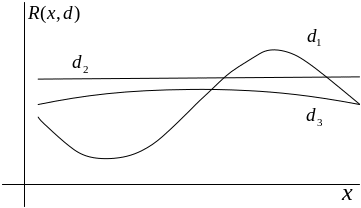
Пример. Решающие функции и не следует рассматривать, так как они доминируются функциями и :

и ;

и .

и ;

и .

Рандомизированные решающие правила

Пусть множество состояний природы , множество решающих правил . Таблица рисков имеет вид:

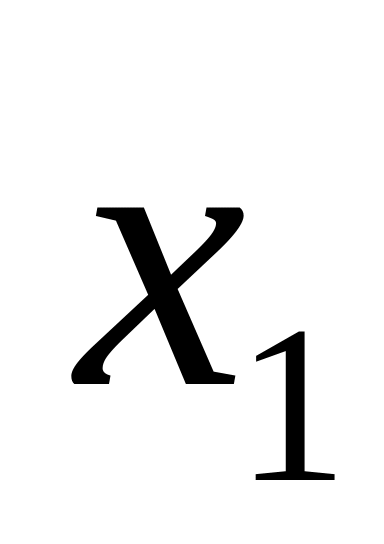
	4	1	3
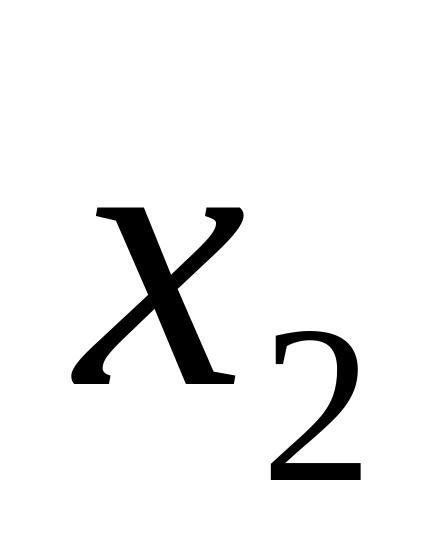
	1	4	3

Расширим множество решающих правил , введя в рассмотрение рандомизмрованное решающее правило :

.

Тогда ,

; .

На рисунке ниже показано графическое представление рисков для рассматриваемых решающих правил.

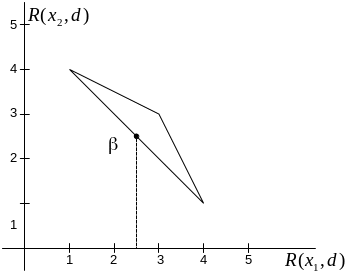
Из того, что и следует, что . В этом случае может быть исключено из дальнейшего рассмотрения.

Ниже будет показано, что всегда существует нерандимизированное решающее правило, которое не хуже, чем рандоимзированное.

Далее в множество решающих правил мы будем включать также и все рандомизированные решающие правила такие, что с вероятностью принимается решение , а с вероятностью - решение :

, где .

Тогда риск от решающего правила равен:

.

При рандомизации по решающим правилам :

,

где , , .

Геометрическая интерпретация

Пусть природа может находиться в M состояниях .

Введем в рассмотрение множество :

.

В множество будем включать риски относящиеся ко всем . Множество - выпуклое множество, т. к. так как в него включены образы рандомизированных правил. Любой отрезок, соединяющий некоторые точки из множества (см. рисунок ниже)

и

и ,

описывается как , где , а это есть не что иное, как точки рисков решающих правил, получающихся рандомизаций решающих правил и , т.е . .

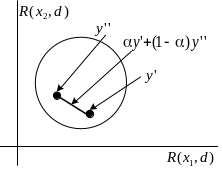
Осторожные решающие правила

Линии равного уровня риска вида представляют собой «прямой угол» с равными сторонами (см рисунок ниже).

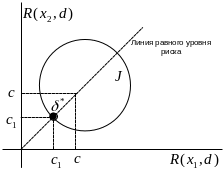
Точка есть точка касания границы множества линией равного уровня с минимальным значением .

Минимаксное решение может быть не единственным, однако очевидно, что в этом случае не все решающие правила допустимы.

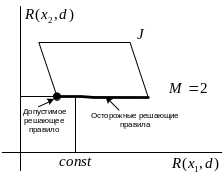
Байесовские решающие правила

Линии равного уровня байесовского (среднего) риска представляют собой прямые вида , идущие с северо-запада на юго-восток.

Для многомерного случая линия равного уровня байесовского риска представляет собой гиперплоскость, которая задается уравнением .

Точка есть точка касания прямой с минимальным значением границы множества .

Ниже приведены примеры байесовских решающих правил.

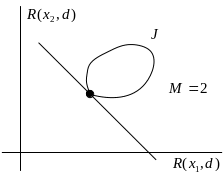
Пример. Пусть множество состояний природы , множество решающих правил и пусть задана таблица рисков .

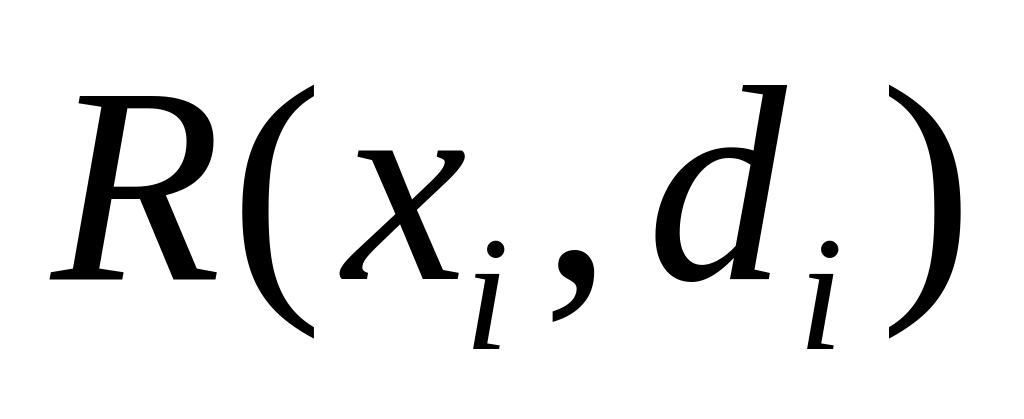
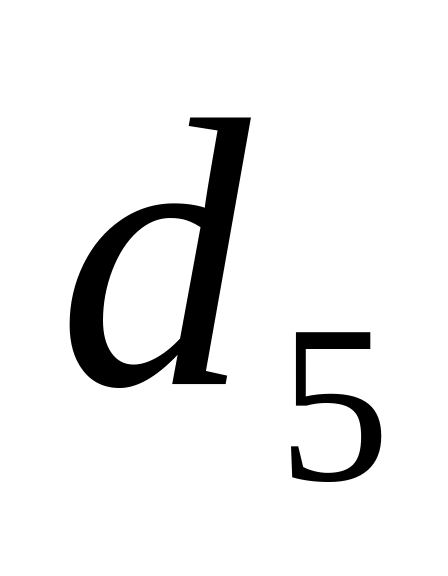
	0	4	2	1	5
	4	5	0	1	4

На рисунке ниже показаны решающие правила и соответствующие им риски.

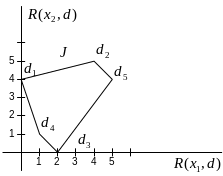
Здесь минимаксное решающее правило есть , обеспечивающее значения минимаксного риска. Байесовское решающее правило определяется значениями вероятностей и :

, .

Рассмотрим (1) для различных значений :

- - это есть вертикальная прямая;

- - это есть горизонтальная прямая;

- и

Подставив значения в уравнение (1) получаем, что равенство справедливо для решающих правил и :

;

;

Таким образом получаем линию .

- и имеем линию равного уровня .

В таблице ниже приведены байесовские решающие правила для различных значений

	Байесовское решающее правило	Риск
	(единственное)
	, (любая рандомизация)	1
	(единственное)	1
	, (любая рандомизация)	1
	(единственное)

Единственность, допустимость, решающая функция

Будем рассматривать случай . - вероятности соответствующих состояний природы.

Теорема 1. Если байесовская решающая функция единственная, то она допустима.

Доказательство (от противного)

Пусть существует , такое что и .

Тогда . Если имеет место строгое неравенство (<), тогда - не является байесововским решающим правилом. Если имеет место равенство, тогда - не является единственным решающим правилом. Следовательно, предположение неверно.

Теорема 2. Если - байесовская решающая функция по отношению к распределению , где , то - допустимо. Распределение - не вырождено.

Доказательство (от противного)

Пусть , такое что и ; ; . Тогда и не является байесовым решающим правилом. Следовательно, предположение неверно.

Теорема 3. Если - допустимое решающее правило, то найдется такое распределение , что , то есть будет байесовским решающим правилом по отношению к .

Покажем для

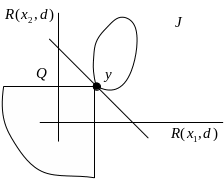
Пусть - допустимая точка. - допустимое решающее правило.

Пусть - множество точек, доминирующих над . Множества и пересекаются только в точке , иначе не будет допустимой точкой. Это означает, что точка лежит на границе : . Поскольку - выпукла, то существует проходящая через точку прямая (гиперплоскость), касательная к . Эта прямая имеет вид , где , , , так как по построению разделяет юго-западную и северо-восточную полуплоскость. Такая прямая существует, поскольку и выпуклы.

Теорема 4. Если минимаксное решение правило единственное, то оно допустимо.

Доказательство(от противного)

Пусть существует , так что и . Но тогда .

Строгое неравенство не может выполняться, иначе не минимаксное решающее правило. Равенство не может выполняться, т.к. будет нарушено условие единственности. Следовательно, предположение неверно, что и требовалось доказать.

Теорема 5. Если - допустимо и , но - минимаксное решающее правило.

Доказательство (от противного)

Пусть существует , такое что . Так как , то . Тогда ,

то есть - не является допустимым. Следовательно, предположение неверно, что и требовалось доказать.

Теорема 6 (Нестрого) Байесовская решающая функция для распределения может быть найдена из условия

, где - апостериорный риск, вычисляемый при условии заданной реализации случайной величины .

для непрерывной случайной величины ;

для непрерывной случайной величины .

Доказательство теоремы приводится в приложении.

Апостериорный риск

Определение. Апостериорным риском от принятия решения при условии того, что известно значение наблюдения z, будем называть математическое ожидание потерь:

= – для непрерывной случайной величины ;

= – для дискретной случайной величины ,

где ;

– апостериорная плотность распределения случайной величины .

В соответствии с формулой Байеса

,

где – априорная плотность распределения .

.

Апостериорная вероятность того, что случайная величина , при условии, что случайная величина равна

.

Байесово решение определяется как

.

Для поиска байесовского решения необходимо минимизировать условный риск: .

По определению , применив формулу Байеса, получаем:

. Таким образом, задача сводится к минимизации следующего выражения:

, , что эквивалентно минимизации апостериорного риска: .