Дифференциальные уравнения

30. Существование и единственность решения обыкновенного дифференциального уравнения первого порядка (теорема Пикара).

31. Структура общего решения нормальной системы обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами.

32. Определение устойчивости по Ляпунову. Асимптотическая устойчивость. Теоремы Ляпунова об устойчивости и асимптотической устойчивости. Устойчивость по первому приближению.

33. Применение метода Фурье для уравнения теплопроводности и волнового уравнения.

34. Типы уравнений с частными производными второго порядка. Теорема о приведении уравнений с двумя переменными к каноническому виду.

35. Простейшая задача вариационного исчисления. Уравнение Эйлера. Первые интегралы уравнения Эйлера.

Теория вероятностей

36. Понятие вероятностного пространства. Примеры вероятностных пространств. Условная вероятность, формула полной вероятности, формула Байеса.

37. Независимые события. Формула Бернулли для вероятности числа успехов, математическое ожидание и дисперсия числа успехов.

38. Функция распределения случайной величины. Типы функций распределения. Свойства и примеры функций распределения.

39. Математическое ожидание и дисперсия случайной величины. Примеры (распределения Бернулли и Пуассона, равномерное и нормальное распределения).

40. Независимые случайные величины. Неравенство Чебышева. Закон больших чисел. Теорема Чебышева.

Задания, включенные в программу государственного квалификационного экзамена Раздел «Функциональный анализ и топология»

Задание 1. Обозначим через t(a, b), t[a, b], t[a, b), t(a, b], t(a, +∞), t(-∞, a), t[a, +∞), t(–∞, a], t(a+, b+), t[n, m] топологии, порожденные на множестве действительных чисел R соответствующими семействами множеств:

B={(a, b): a, b R}, B={[a, b]: a, b R}, B={[a, b): a, b R}, B={(a, b]: a, b R}, B={(a, +∞): a R}, B={(–∞, a): a R}, B={[a, +∞): a R}, B={(–∞, a]: a R}, B={(a, b): a, b R, b>a>0}, B={[n, m]: n, m Z}.

Для данного множества A и для заданных топологий опишите множество внутренних точек int A, граничных точек ∂A, точек прикосновения (замыкание) Ā, изолированных точек множества А.

Варианты: 1. А=(–1, 1] U {3}U(4, +∞); t(a, b), t[a, b], t(a, b], t(a+, b+).

2. A= (– ∞, –2] U[2,3)U{4}; t[a, b), t(a, b], t(–∞, a], t[n, m].

3. A= (–2, 0]UN; t(-∞, a), t(a, b], t(a+, b+), t[n, m].

4. A= (– ∞, 2)U[3, 5)U{6}; t[a, +∞), t(–∞, a], t[a, b], t(a+, b+).

Задание 2. Исследуйте на сходимость данные числовые последовательности в указанных топологиях (обозначения топологий даны в задании 1). Укажите все пределы сходящихся последовательностей.

Варианты: 1. х_n= , y_n = 2ⁿ ; t(a, b), t[a, b], t(a, b], t(a+, b+).

2. х_n= , y_n = -n; t[a, b), t(a, b], t(–∞, a], t[n, m].

3. х_n= , y_n = ; t(-∞, a), t(a, b], t(a+, b+), t[n, m].

4. х_n= , y_n = (–1)ⁿ n; t[a, b), t(–∞, a], t[a, b], t(a+, b+).

Задание 3. Докажите, что приведенные функций определяют нормы на множестве Х. Исследуйте эти нормы на эквивалентность:

Варианты: 1. Х=С[0, 1]; .

2. Х=С¹[0, 1]; .

3. Х=С¹[0, 1]; .

4. Х=l¹ ;

Задание 4. Докажите, что

Варианты: 1. l^p  l^q для любых 1≤p<q, причем l^p ≠ l^q .

2. l^∞  l^p для любых p≥1, причем l^∞ ≠ l^p .

3. L^q[0, 1]  L^p[0, 1] для любых 1≤p<q, причем L^q[0, 1] ≠ L^p[0, 1].

4. L¹[0, + ∞) L²[0, + ∞) и L²[0, + ∞) L¹[0, + ∞)

Задание 5. Исследуйте на сходимость последовательность в соответствующих пространствах. Найдите пределы последовательностей, если они сходятся.

Варианты: 1. .

2. .

3. со стандартной нормой и с нормой .

4. .

5. , Х= s, l^p , l^∞, c, c_o.

6. Х= l¹ и Х= l^∞.

7. Х= l² и Х= s.

Задание 6. Проверьте, будет ли множество Е замкнутым в пространстве Х и постройте его замыкание.

Варианты: 1. X = l^∞ , E = Ф или Е = l¹.

2. X = l² , E = Ф или Е = l¹.

3. X = C[0, 1] , E = P[0, 1].

4. X = L¹[0, 1], E = C[0, 1] .

5. X = C[0, 1] , E = {xC[0, 1]: x(0)=0}.

В задании символом Ф обозначается множество финитных последовательностей.

Задание 7. Найдите нормы следующих функционалов в пространстве Х, если они ограничены.

Варианты: 1. X = С[0, 1] и X = L²[0, 1], .

2. X = С[0, 1] и X = L²[0, 1], .

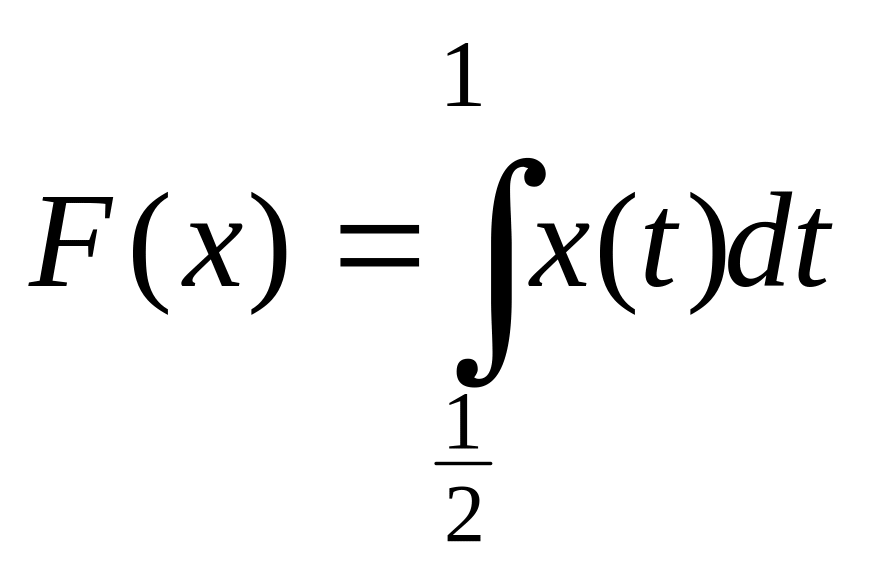3. X = С[0, 1] и X = L²[0, 1], .

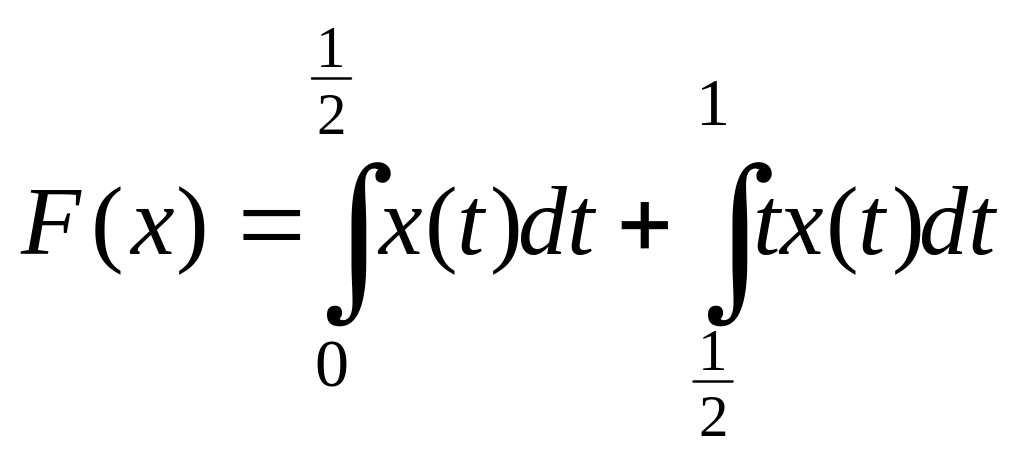4. X = C¹[0, 1] со стандартной нормой и нормой, индуцированной из С[0, 1], .

5. Х= l¹ c нормой индуцированной из пространства l², .

Задание 8. Найдите оператор, сопряженный к оператору A: H → H.

Варианты: 1. H = L²[0, 1], .

2. H = L²[0, 1], .

3. H = l², .

4. H = l², .

Задание 9. Исследовать на предкомпактность множество Е в пространстве Х.

Варианты: 1. X=C[0, 1], .

2. X=C[0, 1], .

3. X = l², .

4. X = l², .

Задание 10. Найдите собственные значения и собственные векторы оператора А, заданного в пространстве Х.

Варианты: 1.

2.

3.

4. Х = l², .

5. Х = l², .

Задание 11. Найдите спектр оператора А и его части.

Варианты: 1. Х=l², .

2. X=C[0, 1], .