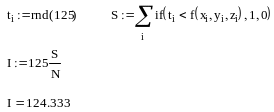Метод Монте-Карло

Метод Монте-Карло занимает особое положение среди методов вычисления определенных интегралов по двум причинам. Во-первых, это единственный метод, позволяющий вычислять интегралы высокой кратности. И, во-вторых, это метод, который дает лишь вероятностные гарантии степени точности вычисления интегралов. В этой лекции приводится описание простейшего варианта метода и без математических доказательств.

Пусть задана некоторая подынтегральная функция – непрерывная в области интегрирования . Выберем в этой области случайных точек М, найдем значение заданной функции в некоторой «средней» точке области интегрирования. При достаточно большом можно считать, что

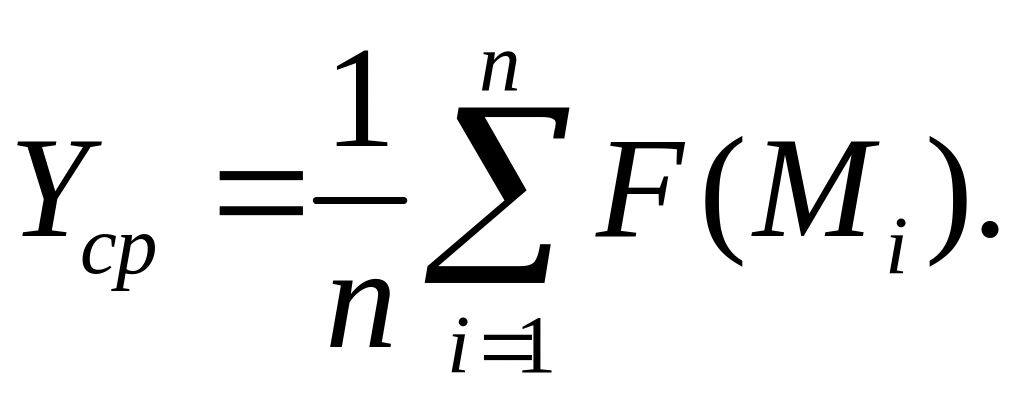
Тогда значение интеграла приблизительно равно где – многомерный объем области интегрирования.

Применим этот метод для простейшего интеграла на промежутке , т.е. необходимо вычислить интеграл (1)

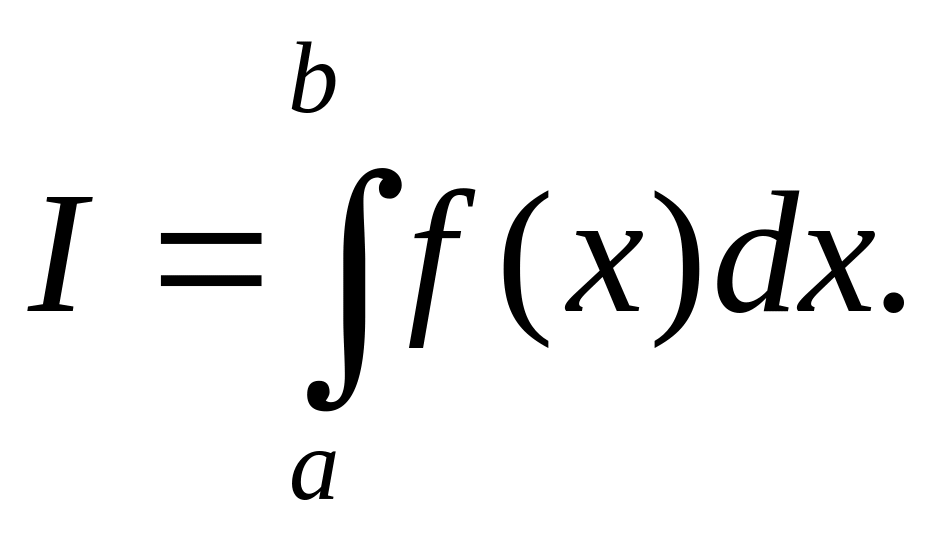
В этом случае в качестве объема области интегрирования выступает длина отрезка , которая равна . Пусть – случайные точки промежутка , тогда значение функции в некоторой «средней» точке будет:

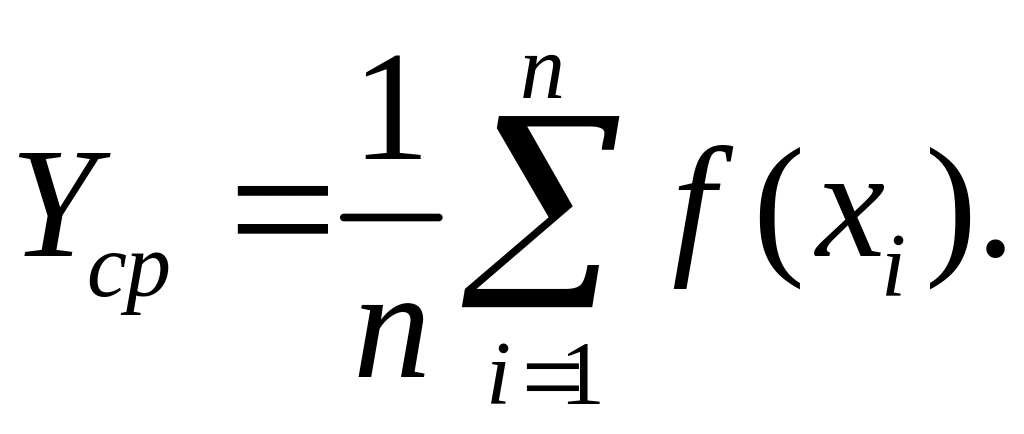
А значение интеграла станет равным

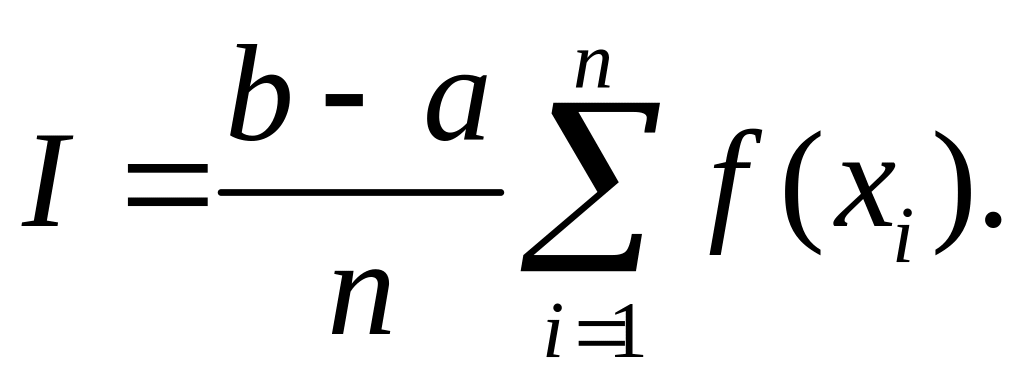
Теперь стоит вопрос оценки точности значения интеграла. Пусть I(f) – точное значение интеграла, а S_n(f) – его приближенное значение, тогда с вероятностью выполняется следующие неравенство

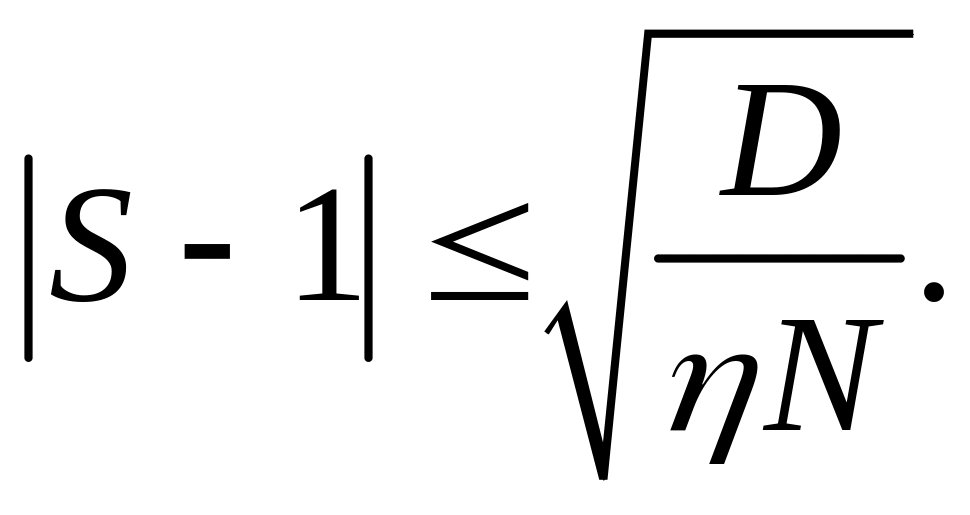
Например, если положить , тогда и модно утверждать, что с вероятностью 99% справедливо неравенство

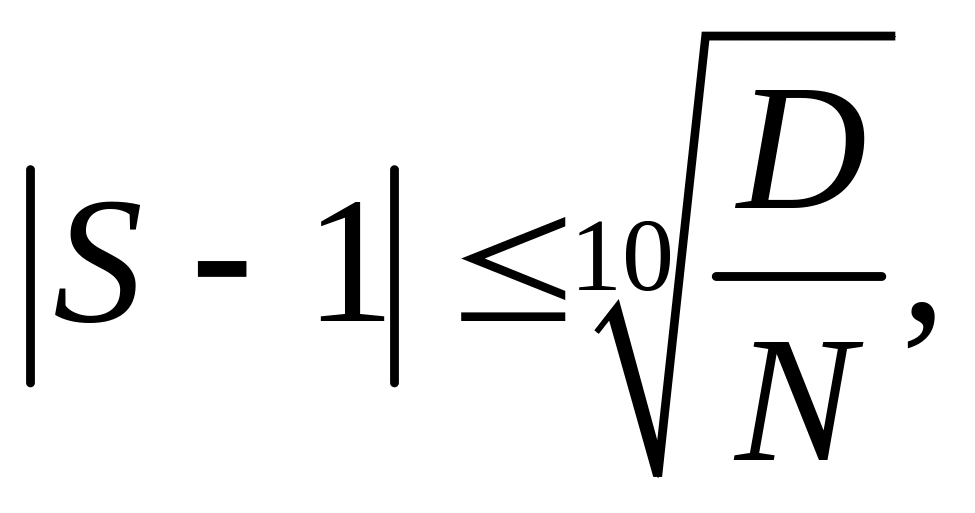
где

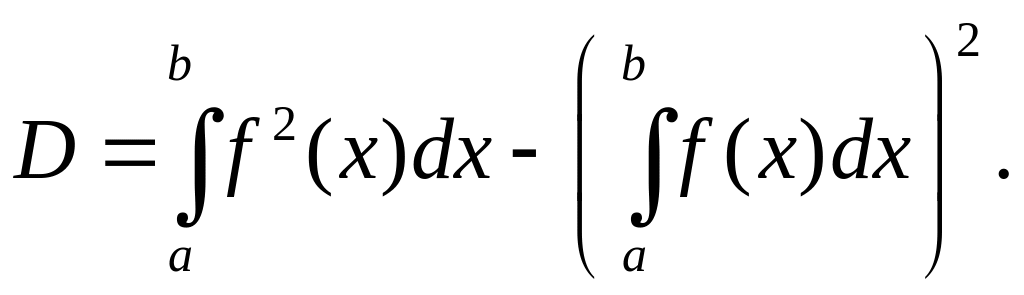
Метод Монте-Карло легко обобщается на интегралы произвольной кратности. Например, двукратный интеграл может быть вычислен по формуле

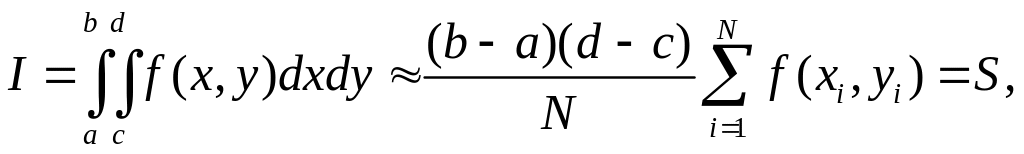
где – случайные числа, равномерно распределенные на интервалах и соответственно. Оценка точности вычисления интеграла совершенно аналогична приведенной выше для случая однократного интеграла.

Хотя Mathcad позволяет вычислять кратные интегралы непосредственно, однако в большинстве случаев при кратности интегралов 3 и более применение метода Монте-Карло предпочтительнее. Дело в том, при одинаковой точности метод Монте-Карло дает существенный выигрыш во времени (в десятки и сотни раз), особенно при большой кратности интегралов. Идея метода состоит в том, что интеграл заменяется величиной F_ср.·V, где V – объем области интегрирования, F_ср. –среднее значение подынтегральной функции, вычисленное по нескольким случайно выбранным точкам.

Определим подынтегральную функцию.

И вычислим интеграл обычным способом

А теперь вычислим тот же интеграл методом Монте-Карло

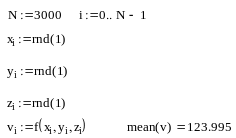
Поскольку в нашем случае объем области интегрирования равен 1, полученное среднее значение совпадает со значением интеграла при некоторой относительной погрешности; время вычисления интеграла по методу Монте-Карло существенно меньше.

Интеграл можно вычислить и другим способом. Заключим область интегрирования внутрь прямоугольной области, и рассмотрим N случайных точек в полученной области. Тогда интеграл найдем из соотношения ,где N – общее число точек, n – число точек, лежащих внутри области интегрирования, V – объем области, включающей область интегрирования.

Максимальное значение подынтегральной функции в области интегрирования не превосходит 125, следовательно, мы может заключить всю область интегрирования внутрь четырехмерного цилиндроида высотой 125 и объемом V=125. Сгенерируем N четверок случайных чисел и подсчитаем, сколько из них лежит под поверхностью f(x,y,z).