Лекция: Парная регрессия и корреляция

Регрессионный анализ представляет собой математический инструментарий для статисти­ческого исследования взаимосвязей между изучаемыми явлениями или показателями, которые носят случайный характер.

Регрессионный анализ применим тогда, когда изучаемые зависимости:

• имеют стохастическую природу, т. е. позволяют устанавливать лишь вероятностные логические соотношения между изучаемыми событиями;

• выявляются на основании статистического наблюдения за анализируемыми событиями.

Регрессионный анализ подразумевается причинную взаимосвязь, т. е. изменения одной перемен­ной (эндогенной) происходят вследствие изменений другой (эк­зогенной).

Функция f(X) называется функцией регрессии у по X (или просто — регрессией у по X), если она описывает измене­ние условного среднего значения результирующей переменной у (при условии, что значения объясняющих переменных X зафик­сированы на уровнях X_i) в зависимости от изменения значений X_i объясняющих переменных.

Математически это записывается так:

y=f(X) = Е(у|Х) (1)

где Е – математическое ожидание.

Основные задачи прикладного ре­грессионного анализа:

1. установление факта наличия (или отсутствия) связи меж­ду переменными, проверка статистической значимости этой связи и исследование ее структуры;

2. прогноз неизвестных значений эндогенной переменной по заданным значениям экзогенных переменных;

3) выявление причинно-следственных связей между объясняющими и результирующими переменными, регулирование значений объясняющих показателей с целью управления результирующими.

Классификация регрессионных моделей представлена на рисунке 1.

Виды регрессионных моделей

Рисунок 1 - Классификация регрессионных моделей

Выбор вида функции регрессии — наиболее важная и наименее теоретически обоснованная часть регрессионного анали­за, которая может включать следующие этапы:

1. качественный (содержательный) анализ информации об изучаемом явлении (ча­сто именно теория предлагает соответствующую структурную и функциональную форму анализируемой зависимости);

2. выявление независимых переменных, которые объясняют изменение исследуемого результативного показателя и определение структурной формы анализируемой зависимости (парная или множественная);

3. определение функци­онального вида анализируемой зависимости (линейная или нелинейная).

Линейная регрессия находит широкое применение ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида

ух = а + bх или ух = а + bх + ε (2)

Уравнение этого вида позволяет по заданным значени­ям фактора х иметь теоретические значения результативного признака подстановкой в него фактических значений фактора х (рисунок 2).

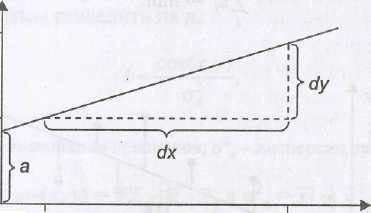
0 х

Рисунок 2 - Графическая оценка параметров линейной регрессии

Построение линейной регрессии сводится к оценке ее пара­метров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами.

Графический метод

По полю корреляции выбирают на графике две точки, проводят через них прямую линию (рисунок 2), затем по графику находят значения параметров. Параметр а определяют как точку пересечения линии регрессии с осью оу, а параметр b оценивают исходя из угла наклона линии регрессии как dy/dx, где dy - приращение результата у ,а dx - приращение фактора х.

Расчетный метод

Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических у_х минимальна, т.е.

(3)

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система нормальных уравнений относительно а и b:

(4)

Можно воспользоваться готовыми формулами, которые втекают из данной системы:

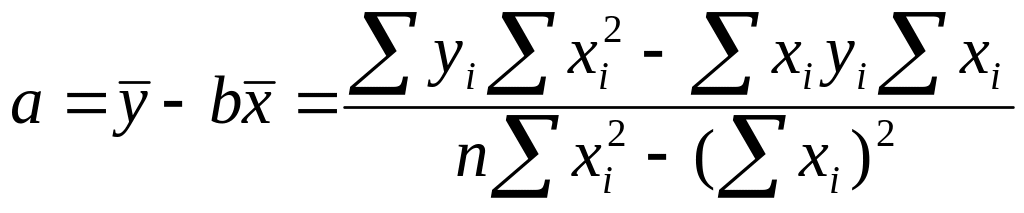(5)

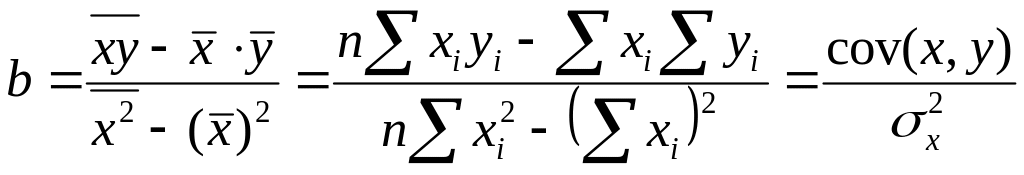(6)

Параметры а и b называются коэффициентами регрессии.

Параметр а – свободный член (масштаб), Формально а=у при х=0. Но если фактор х не имеет и не может иметь 0-го значения, то а не имеет экономического значения. Параметр а может отражать влияние других факторов, не учтенных в модели. Имеет значение знак данного параметра:

• при а>0 изменение результативного признака происходит медленнее, чем фактора (Тр_у < Тр_х);

• при а<0 результат меняется быстрее фактора (Тр_у > Тр_х).

Коэффициент регрессии b показывает среднее изменение результата при изменении фактора на одну единицу. Знак при b показывает направление связи:

• при b>0 связи прямая;

• при b<0 связь обратная.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_ху:

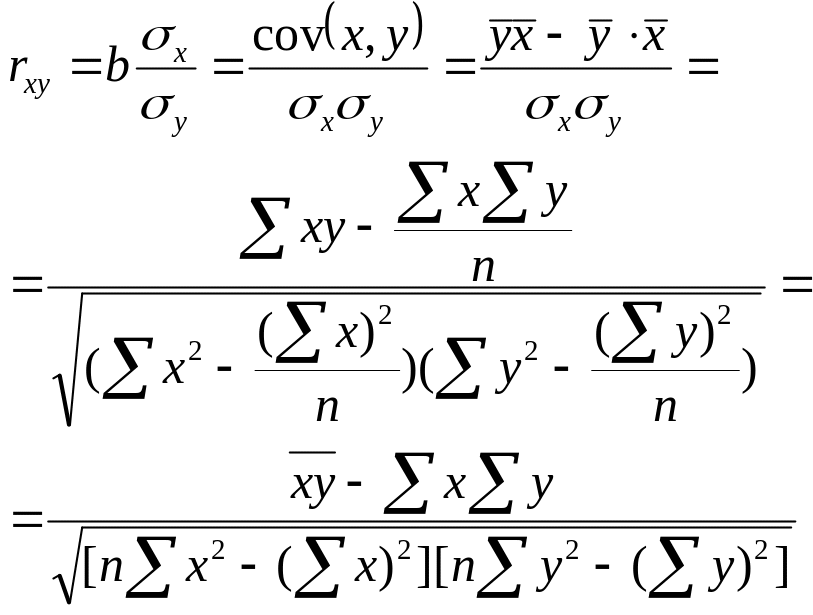(7)

где cov (x,y) – ковариация переменных x и y

σ_x (σ_y) – среднее квадратическое отклонение переменной х (у).

Для линейной регрессии (-1 < r_ху < 1). Знак указывает на направление связи: «+» - связь прямая, «-» - связь обратная. Чем ближе значение коэффициента к «0», тем слабее связь, чем ближе к «±1» - тем сильнее связь. При r_ху=±1 связь функциональная.

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

(8)

где - общая сумма квадратов отклонений;

- сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);

- остаточная сумма квадратов отклонений.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (при линейной зависимости) детерминации.

В общем виде он равен:

(9)

Коэффициент детерминации равен квадрату коэффициента (индекса) корреляции (R²=r²). Он показывает насколько изменение результативного признака у зависит от исследуемого фактора х и какова доля влияния других факторов. Считается, что если R²≥0,5, то модель пригодна для практического применения, т.к. более половины общей вариации результативного признака объясняется воздействием факторнг признака.