
Тема: Ряды динамики
При анализе рядов динамики решаются несколько задач:
находят показатели динамики, характеризующие развитие явления во времени: абсолютный прирост, темпы роста и темпы прироста.
определяют средние показатели в рядах динамики: средний уровень ряда, средний абсолютный прирост, средние темпы роста и прироста.
выявляют основную тенденцию развития при помощи подходящего математического уравнения.
выявляют наличие сезонных колебаний.
1) Для расчета первой группы показателей используются показатели динамики. Они бывают цепными и базисными в зависимости от использования постоянной или переменной базы сравнения. Если в качестве базы сравнения используются уровни предшествующих периодов, такие показатели называются цепными. При использовании неизменной базы сравнения (как правило, первого уровня ряда динамики) рассчитывают базисные показатели динамики.
Показатель |
Способ расчета |
Номер формулы |
|
базисный |
цепной |
||
Абсолютный прирост (+) или сокращение (-) |
|
|
1 |
Темп роста |
|
|
2 |
Темп прироста |
|
|
3 |
или ±Тпр = Тр -100% |
4 |
||
где уi - сравниваемый уровень ряда; уб - уровень явления в периоде, принятом за базу сравнения; уi-1 - уровень явления в предшествующем периоде. |
|||
2) Средние показатели в рядах динамики можно определить следующим образом:
Показатель |
Способ расчета |
Номер формулы |
Средний уровень моментного ряда динамики с равностоящими датами |
|
5 |
Средний уровень моментного ряда динамики с неравностоящими датами |
|
6 |
Средний уровень интервального ряда |
|
7 |
Средний абсолютный прирост |
|
8 |
Средний темп роста |
|
9 |
Средний темп прироста |
|
10 |
где уi - уровень ряда в i-м периоде; n - количество уровней в ряду динамики; ti - промежуток времени, в течение которого уровень i-го ряда динамики оставался неизменным; ∆ уi - цепной абсолютный прирост в i-м периоде; k - количество абсолютных приростов или темпов роста в изучаемом ряду динамики; yn - последний уровень ряда динамики. |
||
3) Наиболее распространенными методами статистического изучения тренда являются:
Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Суть метода – преобразование первоначального ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т.д.)
Метод скользящей средней основан на определении по исходным данным теоретических уровней ряда, в которых случайные тенденции развития выражаются в виде определенной плавной линии. Для этого устанавливаются звенья для исходного ряда, которые должны отвечать длительности внутригодовых циклов в исходном ряду. По звеньям рассчитывают скользящую среднюю по формуле средней арифметической. При вычислении каждой новой скользящей средней «отбрасывают» один уровень ряда слева и «присоединяют» один уровень справа. Полученные значения скользящей средней записывают по середине соответствующего звена.
Для получения обобщенной статистической оценки используется метод аналитического выравнивания заключается в подборе подходящей математической функции и расчете параметров соответствующего уравнения. Подбор адекватной функции осуществляют методом наименьших квадратов, суть которого в минимизации суммы квадратов отклонений между теоретическими (yt) и фактическими (yi) уровнями ряда:
∑( yt - yi)2 →min (11)
Если выравнивание осуществляют одновременно по нескольким уравнениям, наиболее подходящая функция выбирается на основе сравнения стандартизированных ошибок аппроксимации:
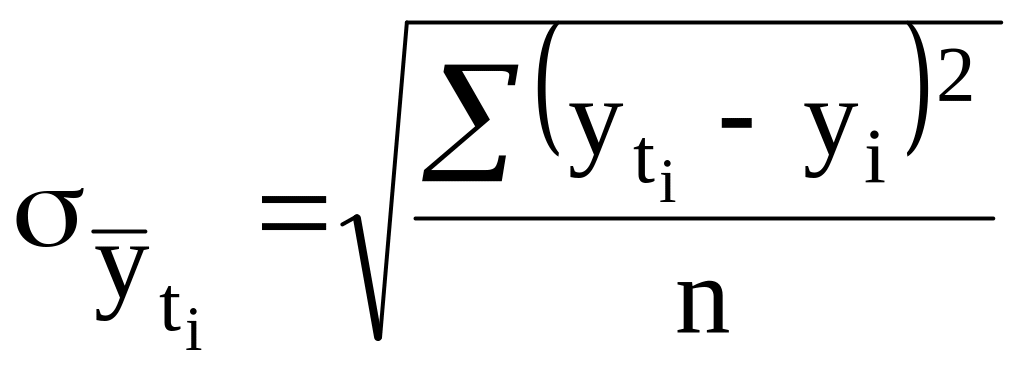 (12)
(12)
В практике статистического изучения тренда различают следующие типы развития социально-экономических явлений во времени:
Тип развития |
Основная характеристика |
Уравнение |
Примечания |
Равномерное развитие |
постоянные абсолютные приросты: ∆yц ≈const |
yt=a0 + a1t (прямая) (13) |
a0 и a1- параметры уравнения; t – время; a1- отражает насколько единиц изменится уровень ряда при изменении t на одну единицу; при a1<0 – происходит равномерное снижение, при a1>0 - возрастание |
Равноускоренное (равнозамедленное) развитие |
постоянное во времени увеличение (замедление) развития: ±Тпрцепной ≈const |
yt=a0 + a1t+ a2t2 (парабола второго порядка) (14) |
а2 – характеризует постоянное изменение интенсивности развития в единицу времени, при a2<0 – происходит замедление роста, при a2>0 – ускорение развития. Значение остальных параметров идентично уравнению прямой. |
Развитие с переменным ускорением (замедлением) |
переменное во времени увеличение (замедление) развития: ±Тпрцепной ≠const |
yt=a0 + a1t+ a2t2+ a3t3 (парабола третьего порядка) (15) |
а3 – отображает изменение ускорения; при a3<0 – ускорение замедляется, при a2>0 – ускорение возрастает. Значение остальных параметров идентично параметрам уравнения параболы второго порядка. |
Развитие по экспоненте |
стабильные темпы роста: Трцепной ≈const |
yt=a0 × a1t (показательная функция) (16) |
a1- темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивность развития. |
Развитие с замедлением роста в конце периода |
цепные абсолютные приросты сокращаются в конце ряда: ∆yц →0 |
yt=a0 + a1×lg t (17) |
a0 и a1- параметры уравнения; t – время
|
Значения параметров уравнения тренда можно определить из системы нормальных уравнений (по методу наименьших квадратов). Примеры расчетов для наиболее распространенных моделей приведены ниже:
Уравнение |
Система нормальных уравнений |
Формулы расчета параметров |
Упрощенные расчеты по методу отсчета от условного нуля (∑t=0) |
|
yt=a0 + a1t (прямая) |
{ |
na0 + a1∑ti =∑yi a0∑ti + a1∑ti2 =∑tiyi |
|
|
|
|
|||
yt=a0 + a1t+ a2t2 (парабола второго порядка) |
{ |
na0 + a1∑ti + a2∑ti2 =∑yi a0∑ti+ a1∑ti2 + a2∑ti3 =∑tiyi a0∑ti2+a1∑ti3 + a2∑ti4 =∑ti2yi |
|
|
|
|
|||
|
|
|||
yt=a0 + a1t+ a2t2+ a3t3 (парабола третьего порядка) |
{ |
na0+a1∑ti+a2∑ti2+a3∑ti3 =∑yi a0∑ti+a1∑ti2+a2∑ti3+a3∑ti4 =∑tiyi a0∑ti2+a1∑ti3+a2∑ti4+a3∑ti5 =∑ti2yi a0∑ti3+a1∑ti4+a2∑ti5+a3∑ti6 =∑ti3yi |
(25) |
|
|
|
|||
|
|
|||
|
|
|||

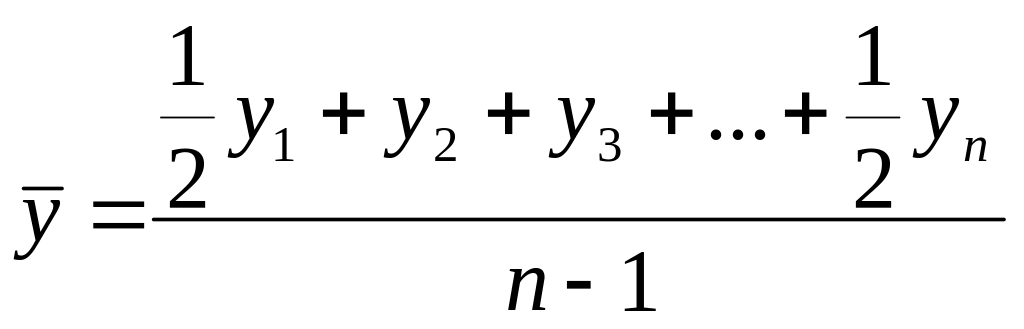
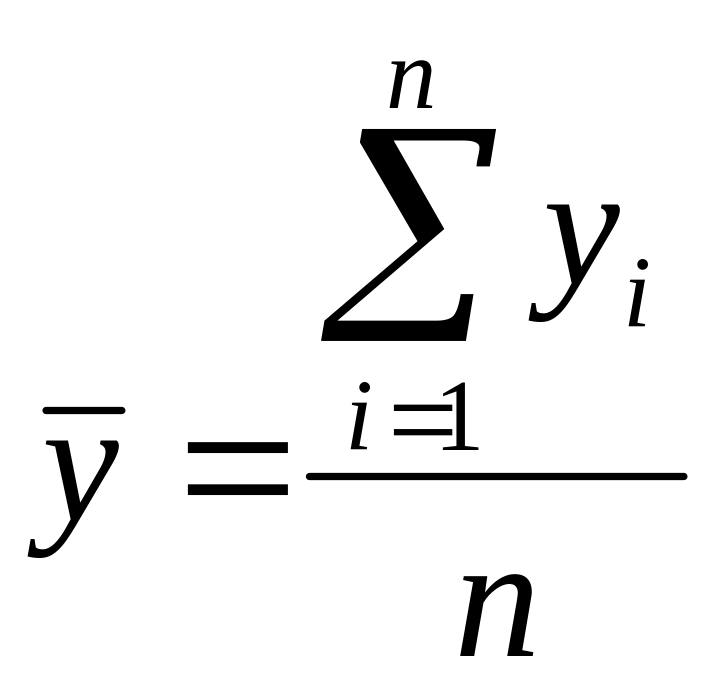
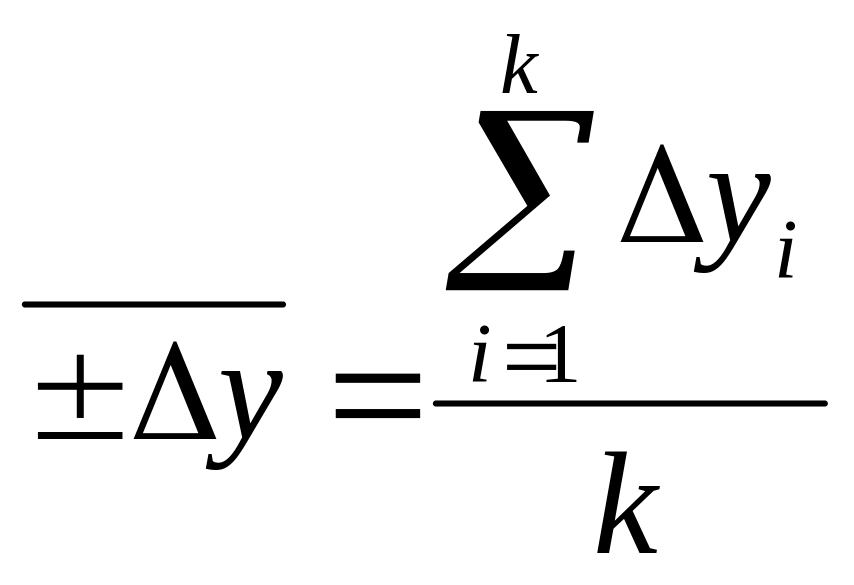 или
или
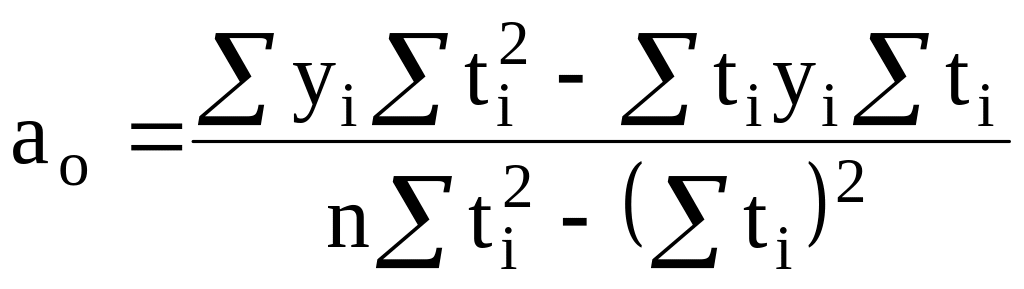 (18)
(18)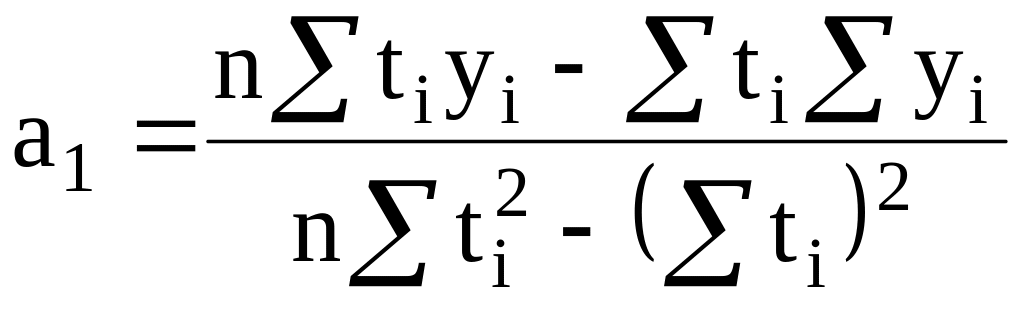 (20)
(20)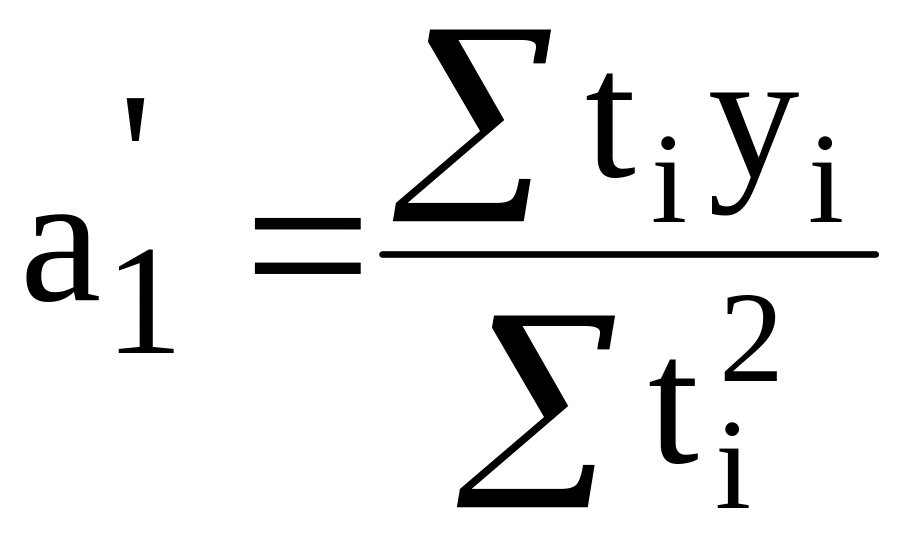 (21)
(21) (22)
(22)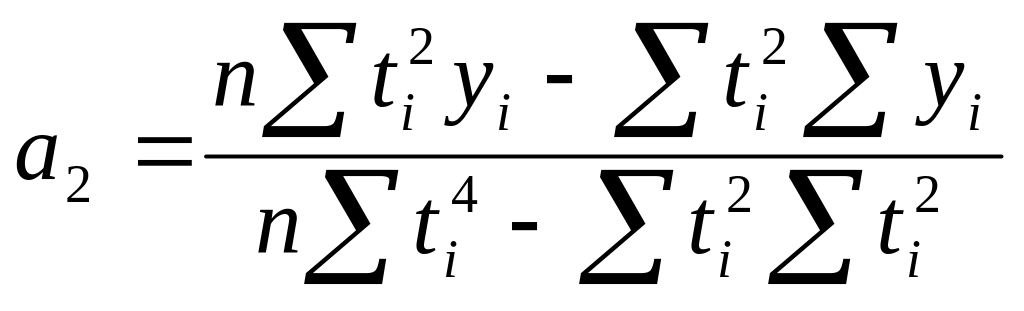 (24)
(24)
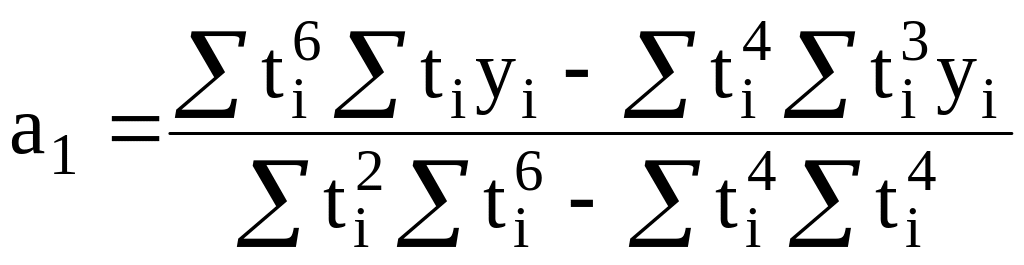 (26)
(26) (27)
(27)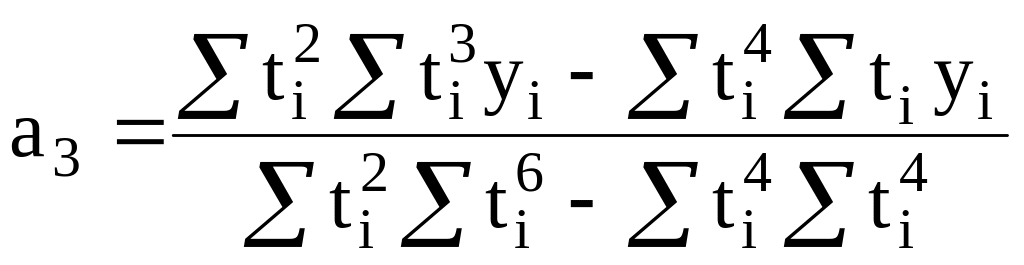 (28)
(28)