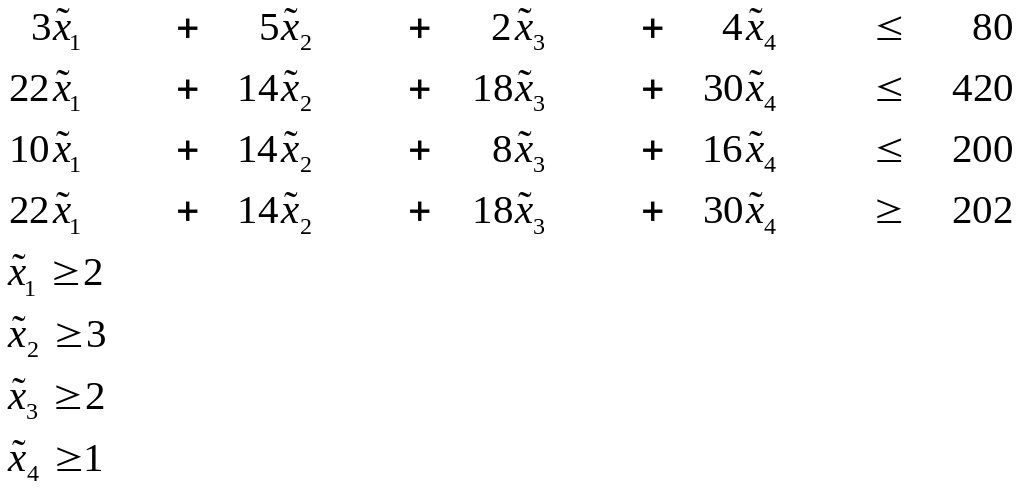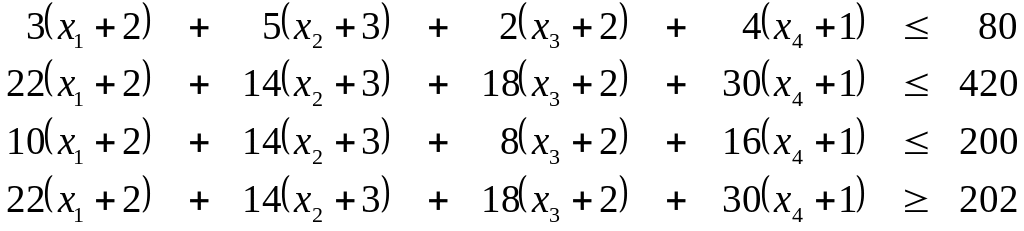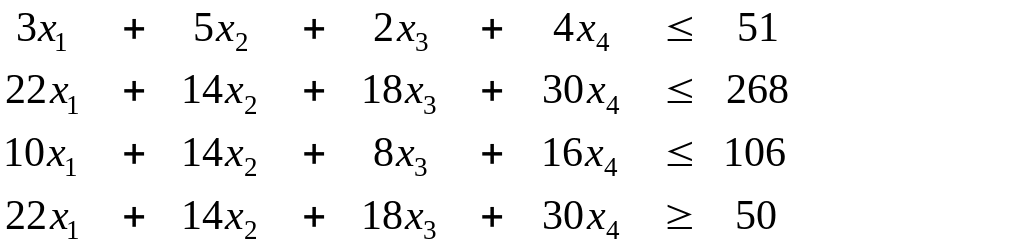Приведение задачи к канонической форме

Задача линейного программирования записана в канонической форме, если она формулируется следующим образом.

Требуется найти вектор , доставляющий максимум линейной форме

(2.5)

при условиях

(2.6) (2.7)

где .

То есть, в канонической форме ЗЛП обязательным является требование максимизации целевой функции (2.5), ограничения задачи должны быть записаны в виде системы линейных алгебраических уравнений (2.6) с неотрицательными правыми частями, а на искомые переменные должны быть наложены условия неотрицательности (2.7).

Нами сформулирована исходная ЗЛП (2.1) - (2.4):

	(2.8)
	(2.9) (2.10)

Для приведения поставленной нами ЗЛП (2.8)-(2.10) к канонической форме необходимо все ограничения (2.9)-(2.10) преобразовать к виду равенств с помощью введения дополнительных неотрицательных переменных.

Число ограничений задачи, приводящих к уравнениям вида (2.6) в нашем случае можно уменьшить, если преобразовать неравенства (2.10) к виду (2.7) используя замену переменных. Для этого перенесем свободные члены правых частей неравенств (2.10) в левые части и введём новые переменные

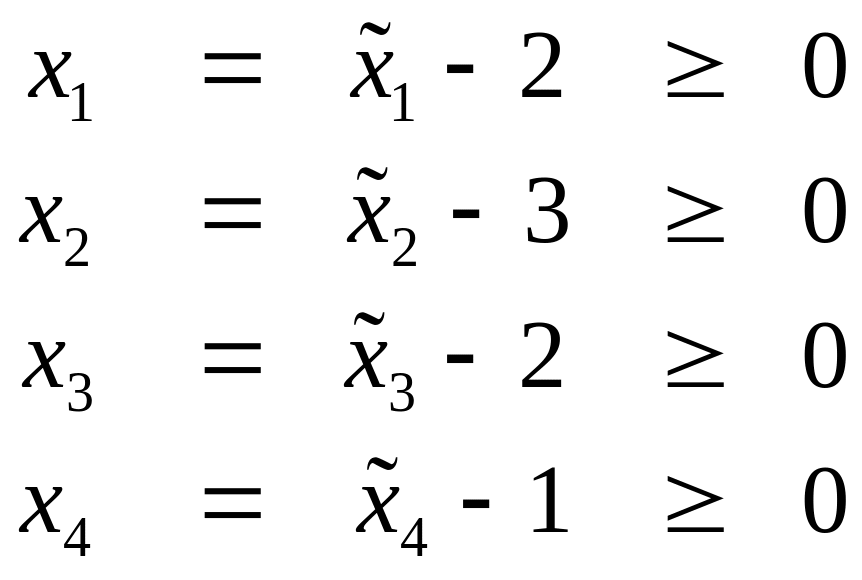
Выразим теперь старые переменные через новые

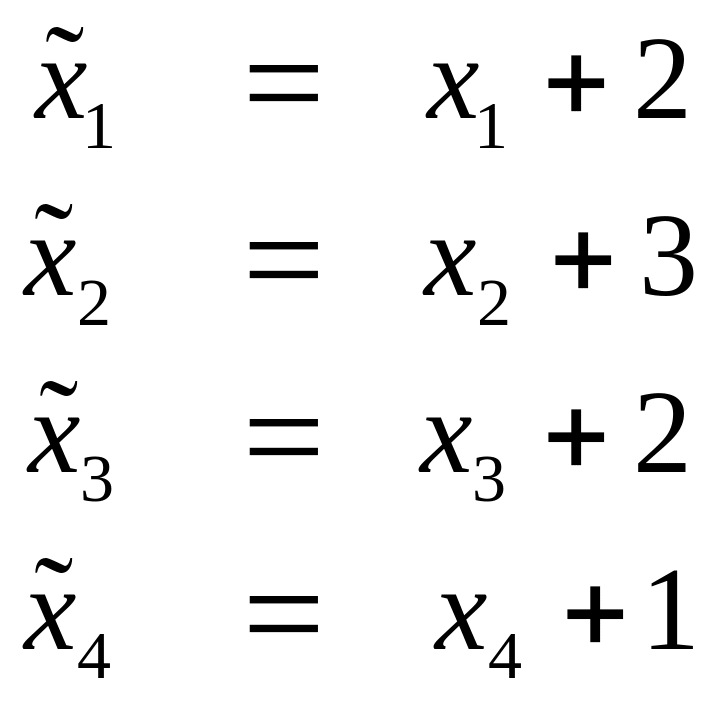
и подставим их в линейную форму (2.8) и систему неравенств (2.9). Получим

Раскрывая скобки и учитывая, что

(2.11)

запишем исходную задачу так:

	(2.12)
	(2.13)
	(2.14)

Для записи неравенств (2.13) в виде уравнений введем неотрицательные переменные , добавляя их в левые части первых трёх неравенств со знаком плюс, а в левую часть последнего неравенства со знаком минус. Тогда задача (2.12) - (2.14) запишется в следующей эквивалентной форме:

	(2.15)
.	(2.16)

Задача (2.15), (2.16) и есть исходная ЗЛП в канонической форме.

Нахождение начального опорного плана

Метод последовательного улучшения плана (так называемый симплекс-метод), который применяется для решения сформулированной ЗЛП (2.15)-(2.16), предполагает знание некоторого исходного опорного плана. Однако, далеко не всегда такой начальный опорный план может быть указан без каких-либо вычислений. Это возможно лишь в случае, когда среди столбцов матрицы условий найдётся достаточное количество таких столбцов, из которых составится единичная матрица и эта матрица будет являться базисом искомого начального плана.

Если же такой возможности нет, то для построения начального опорного плана исходной ЗЛП (2.5)-(2.7) решается вспомогательная ЗЛП (так называемая задача) с расширенным вектором , состоящим из вектора исходной ЗЛП, дополненного искусственными неотрицательными компонентами Последние вводятся в систему ограничений (2.16) так, чтобы сформировался искусственный единичный базис.

Итак, начальный опорный план задачи (2.5) - (2.7) может быть найден с помощью следующей вспомогательной ЗЛП (L - задачи):

	(2.17)
	(2.18)
	(2.19)

Так как матрица условий ЗЛП (2.17)-(2.19) уже содержит единичную подматрицу которая может быть взята в качестве базиса опорного плана, то начальным опорным планом этой задачи будет являться вектор

,

у которого небазисные компоненты а базисные

Решая сформулированную задачу, например, первым алгоритмом симплекс- метода (описание алгоритма приводится ниже в п.4), с указанным начальным планом , в силу ограниченности линейной формы сверху на множестве своих планов ( ) окажется, что процесс решения через конечное шагов приведет к оптимальному опорному плану вспомогательной задачи.

Пуст - оптимальный опорный план задачи, у которого все искусственные компоненты равны нулю. Тогда вектор является опорным планом исходной задачи. Действительно, все дополнительные переменные . Значит, компоненты вектора удовлетворяют ограничениям исходной задачи, т.е. вектор является некоторым планом задачи (2.5) - (2.7). По построению план является также опорным.