Постановка двойственной задачи
Любой задаче линейного программирования определённым образом соответствует некоторая другая задача линейного программирования, называемая двойственной или сопряженной. Первоначальная задач называется исходной или прямой. Тесная связь между исходной и двойственной задачами, составляющими так называемую двойственную пару, проявляется в том, что, зная решение одной из этих задач, можно построить решение другой на основании теоремы о двойственности. Запишем задачи двойственной пары в случае рассматриваемой нами прикладной задачи.
Введём обозначения
:
;
;
|
(2.29) |
;
;
Нашу исходную задачу (2.5) – (2.7) сформулируем, используя матричную форму записи, следующим образом: требуется определить вектор , обращающий в максимум функцию
(2.30)
при условиях
|
(2.31) |
|
(2.32) |
;
.
Тогда двойственная
задача формулируется так: определить
вектор
,
обращающий в минимум функцию
|
(2.33) |
при условии
|
(2.34) |
.Целевая функция (2.33) двойственной задачи может быть записана в эквивалентной форме:
(2.35)
Транспонируя обе
части неравенства (2.34), записанного в
виде строки, и учитывая что
,
ограничения (2.34) двойственной задачи
получим в виде
(2.36)
Отметим, что в
двойственной задаче переменные
могут быть и отрицательными.
Таким образом, для получения двойственной задачи из прямой необходимо выполнить следующие действия:
- транспонировать
векторы ограничений
и коэффициентов линейной формы
и поменять их местами;
- транспонировать
матрицу условий
;
- заменить знаки
равенства в ограничениях (2.31) знаками
неравенств
;
- исключить условия неотрицательности (2.32);
- заменить требование максимизации целевой функции требованием её минимизации.
Выполним эти действия применительно к рассматриваемой нами исходной задаче (2.15), (2.16). Применительно к ней матрицы (2.29) запишутся так :
,
,
;
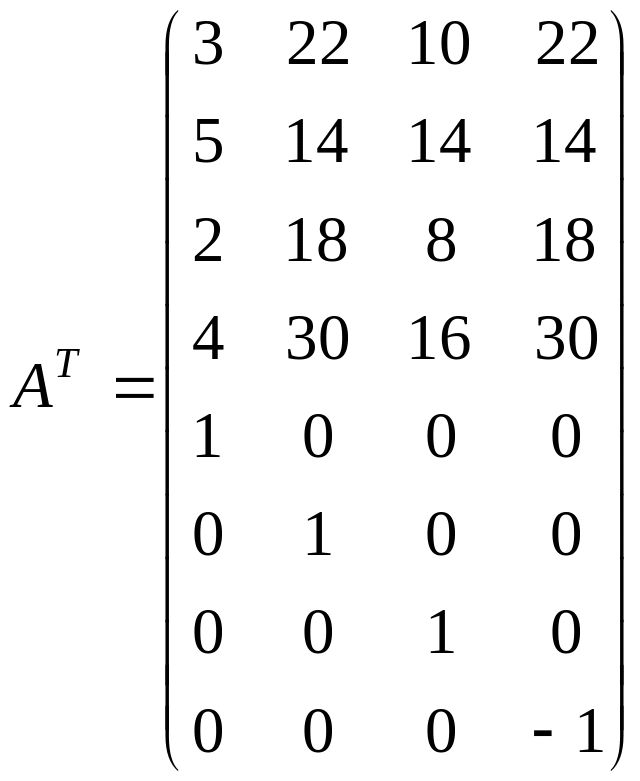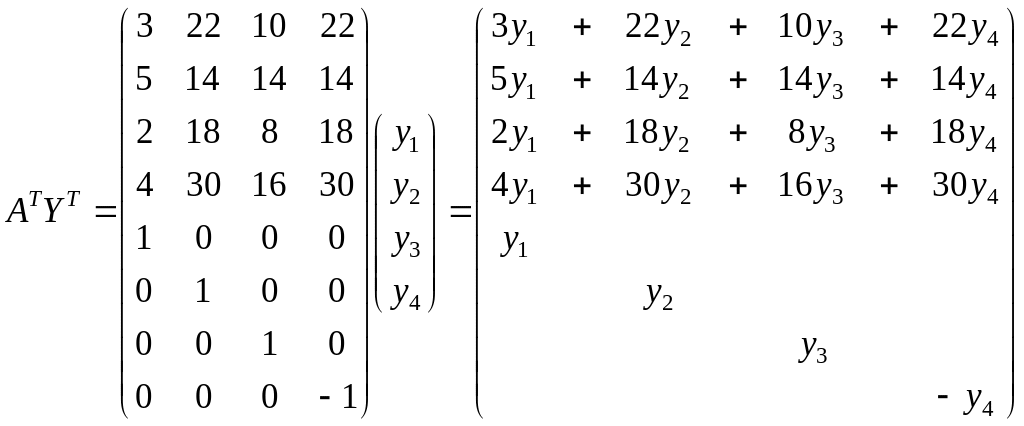
Двойственная задача имеет вид
(2.37)
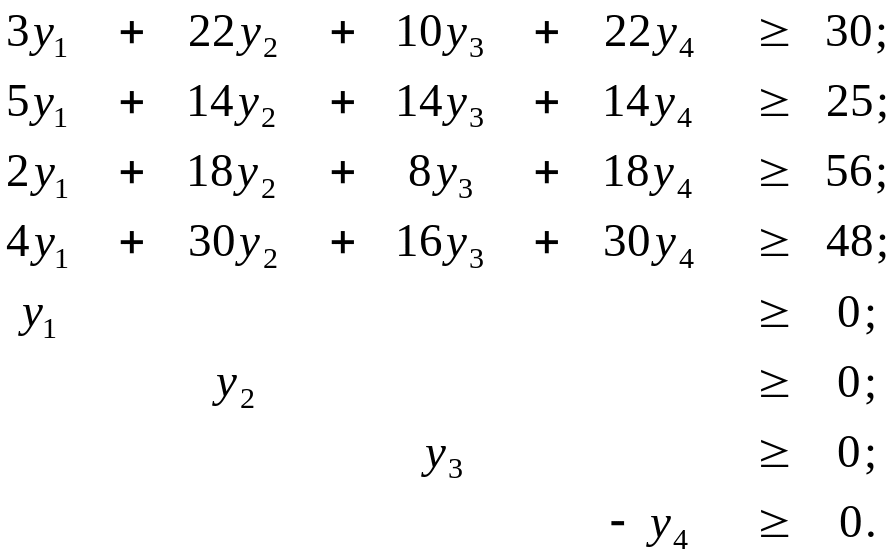(2.38)
Формирование решения двойственной задачи
Для формирования решения двойственной задачи воспользуемся следующей теоремой.
Основная теорема
о двойственности.
Если одна из задач двойственной пары
(2.30) – (2.32) и (2.35) - (2.36) имеет решение, то
другая задача также разрешима. При этом
для любых оптимальных планов
и
(здесь
,
- множества планов соответственно прямой
и двойственной задач) задач (2.30) – (2.32)
и (2.35) - (2.36) имеет место равенство
.
Если же линейная
форма одной из задач не ограничена (для
- сверху, для
- снизу), т.е. не имеет решения, то другая
задача не имеет ни одного плана, т.е.
также неразрешима.
Оптимальное решение двойственной задачи может быть найдено на основе следующего следствия из этой теоремы.
Следствие.
Если вектор
является оптимальным опорным планом
задачи (2.30) – (2.32), то вектор
(2.39)
является оптимальным опорным планом задачи (2.33), (2.34).
Напомним, что в
ходе решения исходной задачи вторым
алгоритмом, на каждой итерации вычисляется
вектор
.
И если
- оптимальный опорный план задачи (2.30)
– (2.32), то в (m+1)-й
строке, соответствующей основной
таблице, находится решение задачи
(2.35)- (2.36).
Итак наша двойственная задача имеет вид (2.37)- (2.38).
Так как исходная задача (2.15), (2.16) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима.
Оптимальным опорным
планом исходной задачи является вектор.
При этом
;
;
.
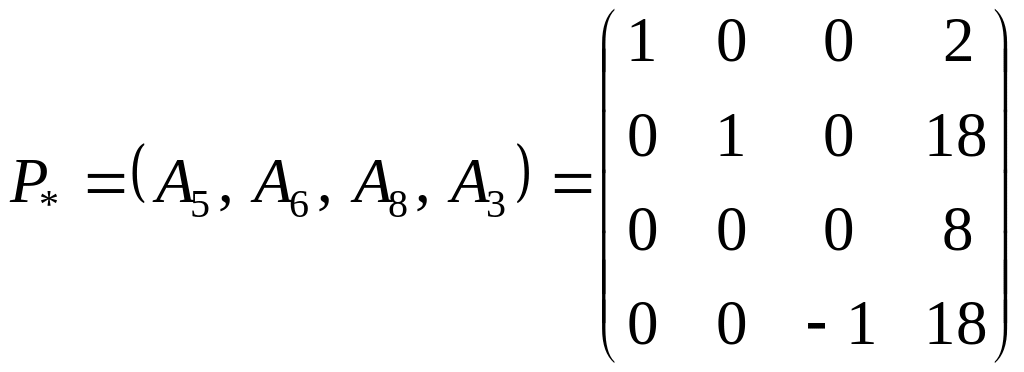Обратная матрица принимает вид
.
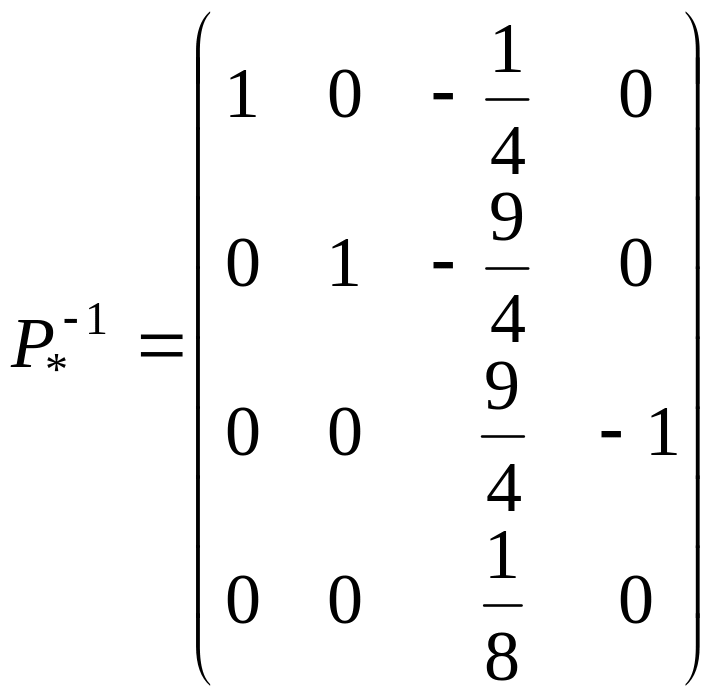В силу следствия
из теоремы о двойственности можно
заключить, что вектор-строка
является оптимальным планом двойственной
задачи, при котором
.
Анализируя (m+1)-ю
строку основной таблицы (см. табл. 6.1,
шаг 3), можно убедиться в том, что
оптимальный план двойственной задачи,
сформированный на основе теоремы о
двойственности, совпадает с оптимальным
планом, найденным при решении исходной
задачи вторым алгоритмом симплекс-метода.
Это говорит о том, что оптимальный план
двойственной задачи (2.37) – (2.38) найден,
очевидно, верно.