35

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ

«ДИСКРЕТНАЯ МАТЕМАТИКА»

(ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ, ЧАСТЬ 11)

СЕВЕРОДОНЕЦК 1997

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ

«ДИСКРЕТНАЯ МАТЕМАТИКА»

(ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ, ЧАСТЬ 11)

для студентов всех форм обучения специальностей

« Компьютерные интеллектуальные системы и сети » ,

«Технология проблемного и системного программирования»

Утверждено

кафедрой ПМ

Протокол № 29

от 12.02.97

Северодонецк СТИ 1997

Методические указания к практическим занятиям по курсу «Дискретная математика» (Элементы теории множеств, часть 11) для студентов всех форм обучения специальностей «Компьютерные интеллектуальные системы и сети», «Технология проблемного и системного программирования»/ Сост. А.Е.Богданов.- Северодонецк: СТИ, 1997.- 35 с.

Составитель А.Е.Богданов

Данные методические указания содержат темы, не вошедшие в первую часть одноименных методических указаний.

Рассматриваемые темы позволят студентам успешно продолжить изучение последующих разделов дискретной математики.

1. Понятие алгебры. Алгебра множеств

Алгеброй A называется совокупность множества M с заданными в нем операциями S={f₁,f₂,…;f_n}, т.е.

A=<M,S>, где M – носитель алгебры, S – сигнатура алгебры, которая включает в себя одноместные, двухместные и другие операции.

Алгебра вида A=<M,f>, где f – двухместная операция, называется группоидом.

Если f – операция типа умножения(x), то группоид называется мультипликативным. Если f – операция типа сложения (+), то группоид называется аддитивным. Здесь знаки (x) и (+) не обязательно означают умножение и сложение чисел. Они просто указывают на то, что над элементами множества (не обязательно числами) выполняются некоторые операции. Эти операции могут лишь внешне напоминать обычные операции умножения или сложения чисел, но по существу в общем случае – это другие операции. Удобство аддитивных и мультипликативных обозначений состоит в том, что при операциях над числами различные соотношения совпадают с общепринятой формой записи.

Элемент e M называется нейтральным элементом группоида A, если для m M выполняется равенство

mfe = efm= m.

Если группоид A=<M,f> мультипликативный, то нейтральный элемент называется единицей и обозначается через 1, если аддитивный, то нейтральный элемент называется нулем и обозначается через 0.

Если множество M содержит нейтральный элемент e относительно операции f , то элемент n называется обратным элементу m ,

если mfn = nfm= e.

Запись =n означает, что обратным элементом m является элемент n.

При аддитивной записи обратный элемент элементу m обозначается через (-m), а при мультипликативной записи–через (m^-1).

Группоид A=<M,f> называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности

m M mfm = m.

Группоид A=<M,f> называется коммутативным или абелевым , если его сигнатура подчиняется закону коммутативности

m,n M mfn = nfm .

Группоид A=<M,f> называется ассоциативным или полугруппой, если его сигнатура удовлетворяет закону ассоциативности

m,n,p M (mfn)fp = mf(nfp).

Полугруппа A=<M,f> , в которой выполнимы обратные операции, называется группой.

Алгебра A=<M, x, +> , которая по умножению является мультипликативным группоидом, по сложению – абелевой группой. причем умножение связано со сложением законами дистрибутивности

m (n + p) = m n + m p

(n + p) m = n m + p m,

называется кольцом.

Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом.

Тело, у которого мультипликативная группа абелева, называется полем.

Пример 1. Аддитивная операция, заданная в множестве M = {a,b,c} , представлена в виде таблицы Кэли

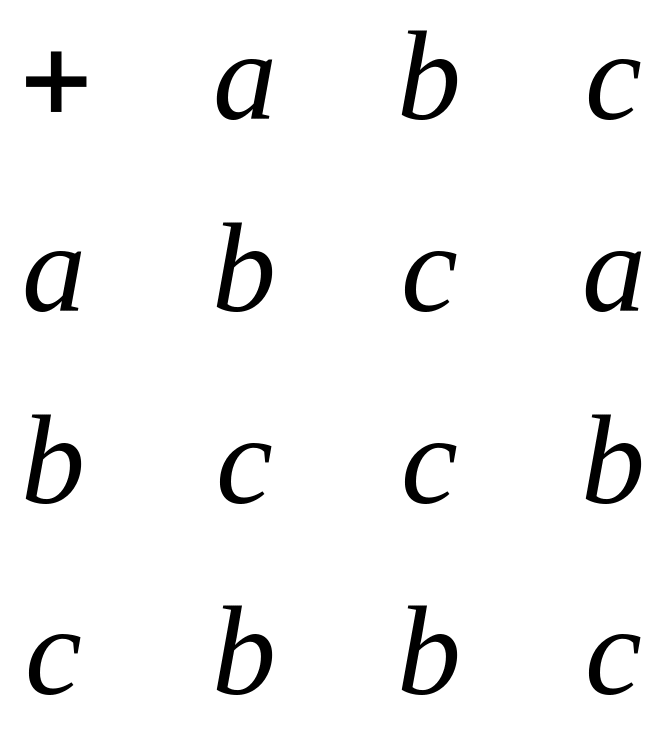
Определить тип группоида A = <M, + > . Указать нейтральные и обратные элементы, если они существуют.

Так как операция (+) , то группоид A = <M, + > является аддитивным. В таблице Кэли на пересечении строки и столбца

стоит результат операции f , т.е. f .

Распишем заданную таблицу Кэли. В нашем примере операция f есть операция типа сложения. Тогда имеем

a + a = b, b + a = c, c + a = b,

a + b = c, b + b = c, c + b = b,

a + c = a, b + c = b, c + c = c. Проверим, является ли группоид A = <M, + > идемпотентным. Для этого должно выполнятся следующие условие:

m M m + m = m .

В нашем случае указанное условие выполняется только для элемента

c M : c + c = c. Для элементов a,b M условие идемпотентности не выполняется: a + a = b, b + b = c. Значит, заданный группоид не является идемпотентным.

Рассмотрим условие коммутативности:

m,n M mfn = nfm.

Имеем: a + b = c = b + a, a + c c + a (a + c = a, c + a = b),

b + c = b =c +b.

Так как a + c c + a, то группоид A = <M, + > не является коммутативным.

Проверим свойство ассоциативности:

m,n,p M (mfn)fp = mf(nfp).

В нашем случае:

(a + b)+c=c + c=c, a+(b + c)=a + b=c, т.е. (a + b)+c = a+(b + c),

(a + c)+b=a + b=c, a+(c + b)=a + b=c, т.е. (a + c)+b = a+(c + b),

(b + a)+c=c + c=c, b+(a + c)=b+ a=c, т.е. (b + a)+c = b+(a + c),

(b + c)+a=b + a=c, b+(c + a)=b + b=c, т.е. (b + c)+a = b+(c + a),

(c + a)+b=b + b=c, c+(a + b)=c + c=c, т.е. (c + a)+b = c+(a + b),

(c + b)+a=b + a=c, c+(b + a)=c + c=c, т.е. (c + b)+a = c+(b + a),

(a + a)+b=b + b=c, a+(a + b)=a + c=a, т.е. (a + a)+b a+(a + b). Условие ассоциативности не выполняется. Значит, группоид A = <M, + >

не является ассоциативным или полугруппой.

По определению элемент e M является нейтральным, если

m M mfe = efm = m.

Указанное условие для элементов множества M не выполняется. Поэтому заданный группоид A не имеет нейтрального элемента. Этим элементом мог бы быть элемент c, т.к.

b + c = c + b = b, c + c = c,

но он не удовлетворяет элементу a множества M, a + c = a, а c + a = b.

Так как группоид A не имеет нейтрального элемента, то он не имеет и обратных элементов.

Имеем единственный результат: аддитивный группоид A = <M, + >.

Пример 2 . В трехэлементном множестве M = {a,b,c} мультипликативная операция задана таблицей Кэли

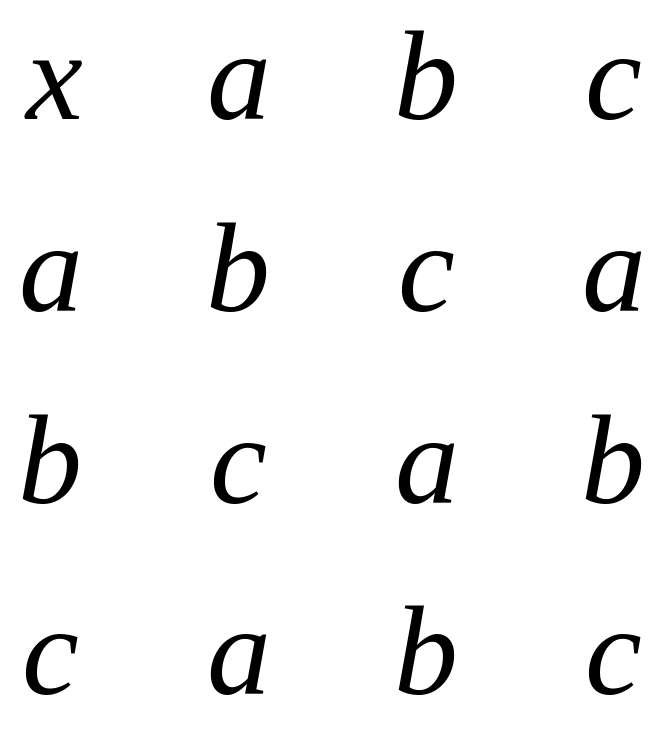
Определить тип алгебры. Указать нейтральный и обратные элементы, если они существуют.

В множестве M задана двухместная операция типа умножения. Значит, алгебра A = <M,x> является мультипликативным группоидом. Уточнить тип алгебры A можно после рассмотрения свойств, которыми обладает ее сигнатура.

Распишем таблицу Кэли

= b, = c, = a,

= c, = a, = b,

= a, = b, = c.

Так как = b и , то группоид не является идемпотентным.

Так как = c= то группоид обладает свойством коммутативности, т.е. он является коммутативным или абелевым группоидом.

Рассмотрим свойство ассоциативности:

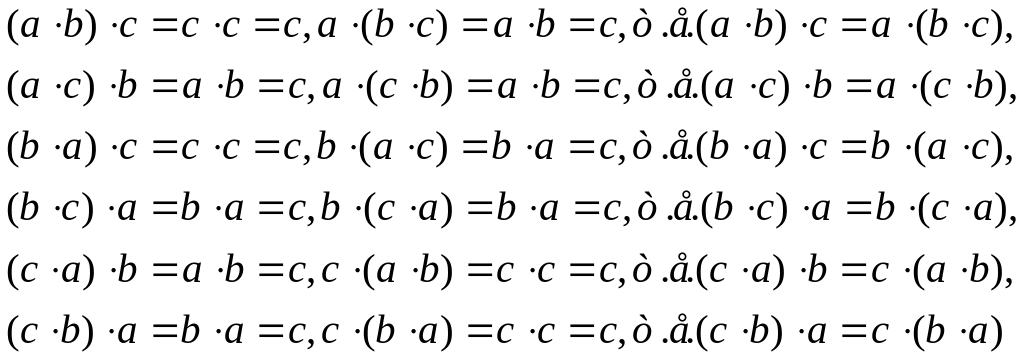
и т. д.

Условие ассоциативности выполняется, значит, группоид A является полугруппой.

Рассмотрим вопрос о наличии нейтрального элемента e в множестве M.

Так как

то нейтральный элемент e существует: e=c. Группоид A = <M,x> мультипликативный, поэтому нейтральный элемент c является единицей.

Тогда обратным элементом a^-1 элементу a будет b, т.е.

a^-1 = b, т.к. а обратным элементу b будет a, т.е.

b^-1 = a, т.к.

Таким образом, алгебра A является группой по умножению. И окончательно, т.к. выполняется закон коммутативности, алгебра

A = <M,x> является абелевой группой по умножению, нейтральным элементом является e = c, обратными элементами являются:

a^-1 = b, b^-1 = a.

Пример 3. Указать тип алгебры, которую образует множество натуральных чисел с заданной в нем операцией сложения.

Нам задан аддитивный группоид A = <N,+> и необходимо уточнить его тип.

В множестве натуральных чисел N справедлив коммутативный закон сложения:

m,n N m+n = n+m.

Значит, заданный группоид является абелевым.

В множестве N выполняется ассоциативный закон сложения:

m, n, p N (m + n)+p = m+(n + p).

Отсюда следует, что абелев группоид является абелевой полугруппой .

Множество натуральных чисел не имеет нейтрального элемента относительно операции сложения, а значит, и обратных элементов.

Таким образом, заданный аддитивный группоид A = <N,+> является абелевой полугруппой по сложению.

Пример 4. К какому типу относится алгебра A = <Z, > , являющаяся совокупностью множества целых чисел с заданной в нем операцией умножения.

В множестве целых чисел выполняются коммутативный и ассоциативный законы умножения. Значит, заданный мультипликативный группоид является абелевой полугруппой по умножению.

Нейтральным элементом e является 1, т.е. e=1, т.к.

m Z

Для m Z обратным элементом(m^-1) будет 1/m,

т.к.

Таким образом, заданная алгебра является абелевой группой по умножению.

Пример 5. Задана алгебра A = <M, +, x> , в которой M={ a,b,c} , а операции: аддитивная (+) и мультипликативная (x) заданы таблицами Кэли:

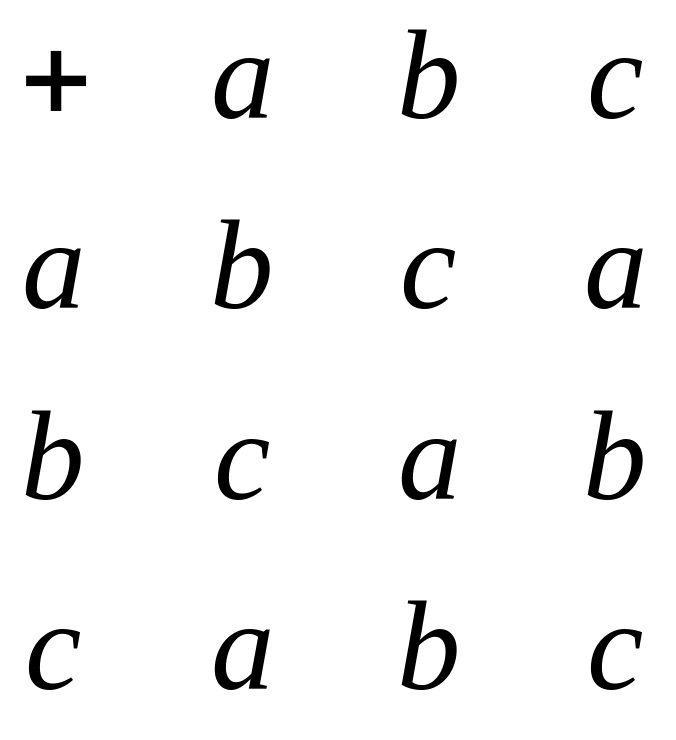
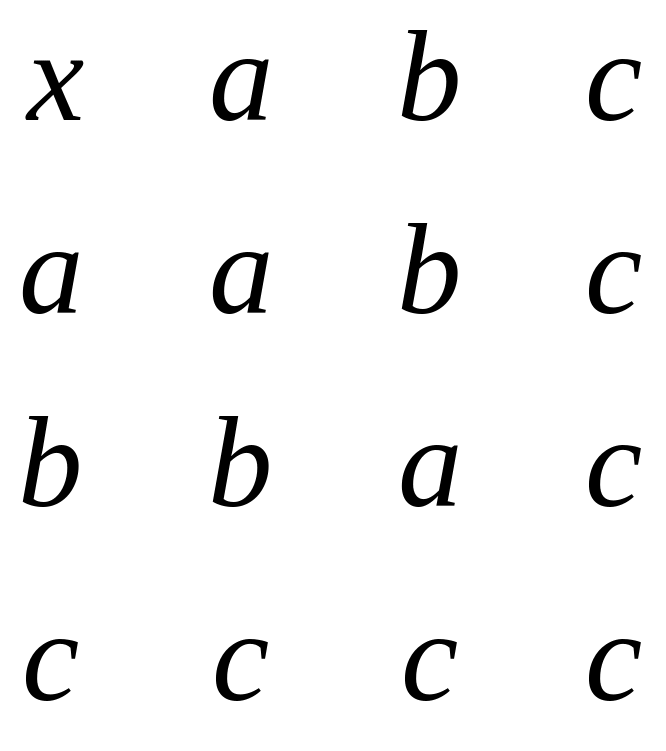
Показать, что M с заданными в нем операциями образует кольцо.

Из определения кольца следует, что алгебра должна быть по сложению абелевой группой. Проверим это. Распишем таблицу Кэли, соответствующую операции (+) :

a + a = b, b + a = c, c + a = a,

a + b = c, b + b = a, c + b = b,

a + c = a, b + c = b, c + c = c.

Проверяем выполнение условия ассоциативности:

(a + b)+c = c + c = c, a+(b + c) = a + b =c, т.е. (a + b)+c = a+(b + c),

(a + c)+b = a + b = c, a+(c + b) = a + b =c, т.е. (a + c)+b = a+(c + b),

(b + a)+c = c + c = c, b+(a + c) = b + a =c, т.е. (b + a)+c = b+(a + c),

(b + c)+a = b + a = c, b+(c + a) = b + a =c, т.е. (b + c)+a = b+(c + a),

(c + a)+b = a + b = c, c+(a + b) = c + c =c, т.е. (c + a)+b = c+(a + b),

(c + b)+a = b + a = c, c+(b + a) = c + c =c, т.е. (c + b)+a = c+(b + a), и т. д.

Закон ассоциативности выполняется, значит, заданная алгебра является полугруппой по сложению.

Так как a + c=c + a=a, b + c=c + b=b, c + c = c, то элемент c является нейтральным элементом относительно операции сложения, т.е. e=c.

Операция (+) является аддитивной, следовательно, c является нулем.

Тогда обратными элементами элементов a, b будут: -a = b, -b = a, т. к. a + b = b + a = c и b + a = a + b = c.

Так как в полугруппе выполнима обратная операция, то она является группой.

Проверим свойство коммутативности:

a + b=c=b + a, a + c=a=c + a, b + c=b=c + b, т.е. указанное свойство выполняется.

Следовательно, группа является абелевой.

Заданная алгебра по умножению является мультипликативным группоидом. Для того, чтобы алгебра A = <M, +, x> была кольцом, осталось показать, что умножение связано со сложением законами дистрибутивности:

Для проверки выполнения этих законов распишем таблицу Кэли, соответствующую операции (x):

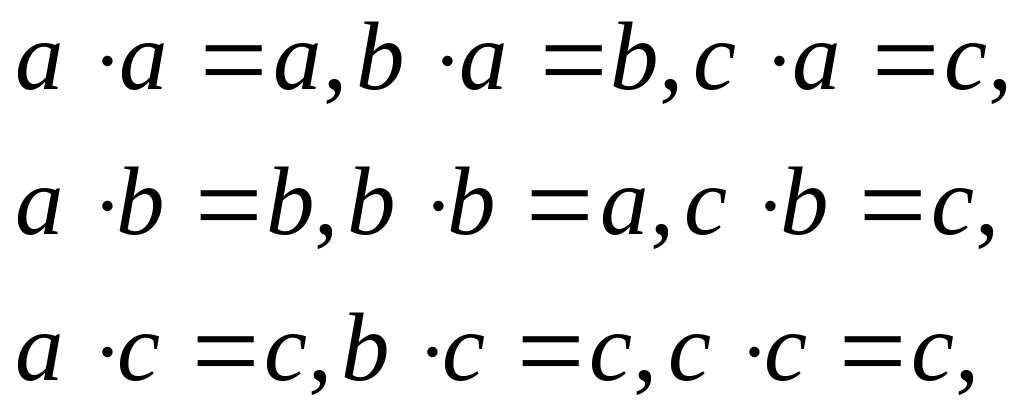
и воспользуемся разложением таблицей Кэли, соответствующей операции (+):

Законы дистрибутивности выполняются. Следовательно, заданная алгебра A = <M, +, x> является кольцом.

Под алгеброй множеств (алгеброй Кантора, булевой алгеброй множеств) понимают алгебру вида

,

где булеан – носитель алгебры, а сигнатура – операции объединения , пересечения и дополнения .

Для операций алгебры множеств выполняются следующие законы и свойства:

1. Коммутативность объединения и пересечения

, .

2. Ассоциативности объединения и пересечения

,

.

3. Дистрибутивности пересечения относительно объединения и объединения относительно пересечения

,

.

4. Идемпотентности объединения и пересечения

5. Действия с универсальным J и пустым множествами

6. Де Моргана

, .

7. Двойного дополнения

.

Алгебра множеств по аддитивной операции объединения и мультипликативной операции пересечения является абелевой полугруппой.

Любая теорема алгебры множеств и, в частности свойства операций над множествами выводятся из первых трех законов и свойств:

,

которые в свою очередь доказываются только в терминах отношения принадлежности.

Пример 6. Доказать закон

.

Для доказательства данного закона используем отношение принадлежности.

Пусть , тогда, согласно определению объединения множеств, или .

Если , то x принадлежит объединению с любым множеством, т.е. и , следовательно, по определению пересечения множеств .

Если , то и по определению пересечения множеств, следовательно, и , т.е. и в этом случае .

Тем самым доказано, что

.

Пусть , тогда и . Если , то x принадлежит объединению с любым множеством, т.е. .Если , то и . Это означает по определению пересечения множеств, что . Тогда x принадлежит объединению с любым множеством, т.е. . Тем самым доказано, что

В соответствии с определением равенства множеств приходим к требуемому закону

.

Пример 7. Доказать, что

.

Данное соотношение доказывается следующими преобразованиями:

Здесь в вертикальных скобках указаны свойства и законы, которые использовались при доказательстве.

Для доказательства законов и других теоретико-множественных соотношений часто используют круги Эйлера.

Пример 8. Доказать закон

с помощью кругов Эйлера.

Для доказательства строим отдельно области, соответствующие левой и правой частям данного выражения. Если построенные области совпадают, то закон считается доказанным.

На рис.1.1а показана область, соответствующая левой части выражения. Здесь вертикальная штриховка соответствует пересечению , а горизонтальная штриховка - M_a. Тогда вся заштрихованная область будет соответствовать объединению этих областей, т.е.

На рис.1.1б изображена область, соответствующая правой части выражения. Здесь вертикальная штриховка соответствует объединению , а горизонтальная штриховка - . Тогда область, в которой встречаются обе штриховки, будет соответствовать пересечению

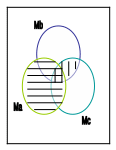
а) б)

Рис.1.1

Сравнение полученных областей показывает, что они совпадают, т.е. закон доказан.

Примеры для самостоятельного решения

1. В трехэлементном множестве M = {a,b,c} аддитивная

операция задана таблицей Кэли

Определить тип алгебры. Указать нейтральный и обратные

элементы, если они существуют.

2. Дана группа A=<M, +>, где M={a, b, c, d, e, f}, а аддитивная операция задана таблицей Кэли

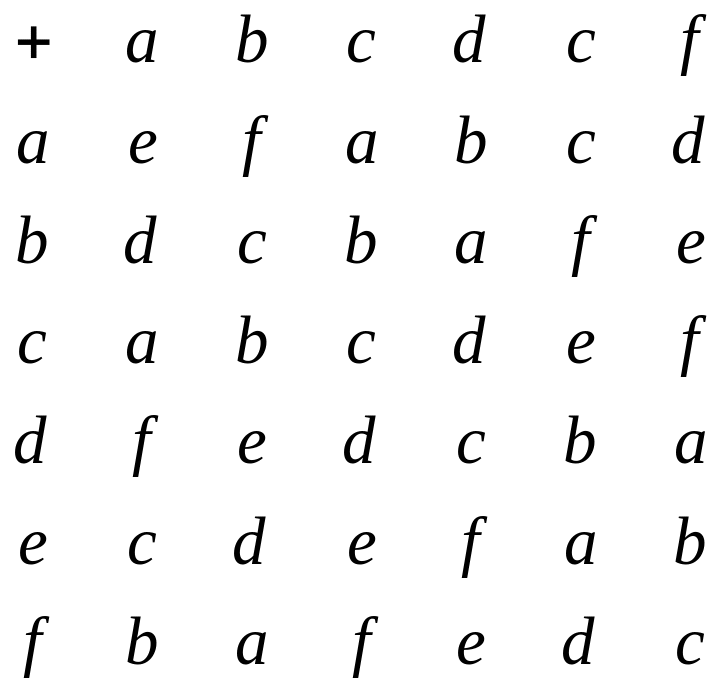
Является ли данная группа коммутативной? Какой элемент из M играет роль нейтрального элемента? Для каждого элемента из M определитель обратный элемент.

3. К какому типу относится алгебра A=<R, > , являющаяся совокупностью множества действительных чисел с заданной в нем операцией умножения.