ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ

"ДИСКРЕТНАЯ МАТЕМАТИКА"

(ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ. ЧАСТЬ I)

для студентов всех форм обучения специальностей "Компьютерные системы и сети" и "Системное программирование"

Утверждено кафедрой ВВМ Протокол № 9 от 31. 05. 2000г.

СЕВЕРОДОНЕЦК СТИ 2000

Методические указания к практическим занятиям по курсу "Дискретная математика" (элементы теории графов, часть I) для студентов всех форм обучения специальностей "Компьютерные системы и сети" и "Системное программирование" /Сост.А.Е.Богданов. - Северодонецк: СТИ, 2000. - 44 с.

Составитель А.Е.Богданов

- 3 -

Теория графов является одним из разделов современной дискретной математики. Теория графов имеет многочисленные предметные интерпретации. Она успешно применяется в задачах управления про­изводством и при проектировании сетей ЭВМ, при разработке совре­менных электронных модулей и при проектировании физических систем с сосредоточенными параметрами (акустических, механических, элект­рических) при решении проблем генетики и проблем автоматизации проектирования (САПР). Теория графов является основой математиче­ского обеспечения современных систем обработки информации. Успешно используется эта теория и в ядерных исследованиях (диаграммная техника Фейнмана) и т.д.

Данные методические указания помогут студентам овладеть основными положениями теории графов и могут служить как дополнение к практическим занятиям, так и одним из источников при самостоятельном изучении студентами теории графов.

- 4 -

I. Первоначальные понятия теории графов

В методических указаниях к практическим занятиям по курсу "Дискретная математика(элементы теории множеств, часть I) граф определялся как совокупность множества М с заданным в нем бинарным отношением , т.е.

В теории графов принята другая запись, а именно

где

носитель V - множество вершин графа, а сигнатура U - множество дуг или ребер графа.

Дуга - это линия с ориентацией, соединяющая две вершины графа. Ребро - это линия без ориентации, соединяющая две вершины графа.

Графи можно разбить на две группы: ориентированные (рис.1.1а) и неориентированные (рис.1.16) графы.

- 5 -

Ориентированный граф (рис.1. la) имеет: множество вершин

множество дуг

Неориентированный граф (рис.1.16) имеет: множество вершин

множество ребер

Дуга (ребро) U, соединенная с вершиной называется инци-дентной вершине , а вершина - коинцидентной дуге (ребру) U

В дуге - начало дуги, - конец дуги.

Две дуги (ребра) называются смежными, если они инцидентны одной и той же вершине.

Вершины графа могут быть соединены двумя и более ребрами или дугами.

- кратные ребра

Граф, содержащий кратные ребра, называют мультиграфом.

кратные дуги кратные дуги

(строго параллельные) (нестрого параллельные)

Каждому неориентированному графу (рис.1.2а) можно поставить в соответствие ориентированный граф (рис.1.2б) с тем же множеством вершин. В этом графе каждое ребро заменено двумя дугами, инцидентными тем же вершинам и имеющим противоположные направления. Такое соответствие называется каноническим.

Любому ориентированному графу G соответствует неориентированнй граф , в котором ребро имеется тогда и только тогда, когда в исходном графе G есть дуга G или дуга .

Рис.1.1

Рис.1.2

Степенью s( ) вершины называется число дуг (ребер) инцидент­ных этой вершине.

Граф может иметь петли:

ڤ Зная множество вершин V и множество дуг U , всегда можно построить граф (рис.1.3)

Петля дает в степень вершины вклад 2.

Граф называется однородным степени k, если степени всех его вершин равны k .

Граф без петель и кратных ребер (строго параллельных дуг) на-зывается простым графом, с петлями и кратными ребрами (строго параллельными дугами) - псевдографом.

Граф называется полным, если все его вершины попарно смежны. Пример I. Задан ориентированный граф G=< V,U>, которого

Является ли заданный граф G полным, однородным? Определить сте­пень вершины .

Рис.1.3

Заданный граф G не является полным, т.к. не все вершины попарно смежны: вершины и не смежны. Граф G не является однородным, т.к. не все степени его вершин имеют одинаковое зна­чение. Степень вершины равна 4, т.е. s( ₂) =4, т.к. этой вершине инцидентны две дуги и эта вершина имеет петлю. ■

Граф называется двудольным, если множество его вершин V разбито на два непересекающихся подмножества V₁ и V₂ так, что каждое ребро (дуга) в G соединяет две вершины из разных подмножеств (рис.1.4а).

Двудольный граф называется полным, если каждая вершина из V₁ соединена с каждой вершиной из V₂ и наоборот и обозначается К_{т п} , где т - число вершин V₁ , а n - число вершин V₂ (рис.1.4б)

Ряс.1.4

Граф К_{т п} имеет m+n вершин и m - n ребер. Граф К_1,n называется звездным графом.

Пример 2. Является ли граф G= <V, U > , у которого V=

={a, b, c, d, e, f}, U={(a,d),(b,d), (b,e),(b,f), (c,e), (c,f)} двудольным? Является ли заданный граф полным?

□ Заданный граф является двудольным, т.е. множество вершин V можно разбить на два непересекающихся подмножества V₁={a,b,c} и V₂ = {d, e, f} так, что заданные ребра соединяют только

вершины из разных подмножеств (рис. 1.5).

Двудольный граф не является полным, т.к. вершина a из V₁ не соединена с вершинами d и f из V₂ , а вершина С из V₁ не соединена с вершиной d из V

Для учета изолированных вершин, т.е. вершин не коинцидентных ни одной дуге (ребру), расширим понятие графа G до совокупности вида

где унарное отношение U₁ определяет изолированные вершины, U₂ - дуги или ребра (рис. 1.6). Здесь U₁ = { }.

Граф G'= является частью графа G= <V, U₁ ,U₂ >, если . Часть графа G' может совпадать с самим графом G (также как в теории множеств M M).

Если V'=V, U^' = U₁, , то часть графа G' графа G -называется суграфом.

Граф, полученный из графа G удалением некоторых вершин и инцидентных им дуг (ребер) называется подграфом графа G

Подграф также является частью графа.

Пример 3. Задан неориентированный граф у которого ,

Изобразить одну из возможных частей графа G , один из возможных суграфов графа G и один из возможных подграфов графа G □ Сначала изобразим заданный граф (рис.1.7).

Рис.1.7

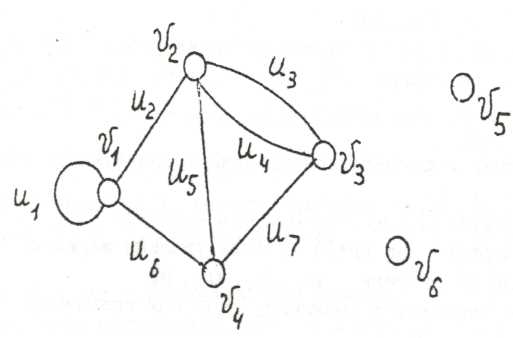
Рис.1.5

Рис.1.6

Здесь для кратности дальнейшей записи ребра обозначены через u₁. u₂ …. u_7. Часть графа изображена на рис.1.8а, суграф -на рис.1.8б подграф - на рис.1.8в.

начается Г . Тогда граф G можно определить как совокупность множества вершин и множества их окрестностей, т.е.

Пример 4. На рис. 1.9 изображен граф G . Определить окрестность вершины этого графа.

Рис 1.8 4

Часть графа получена из графа G путем удаления ребер u₁, u₂, u₃, u₄, u₅ u_{6 ,} u₇ и вершин , т.е. { u₁, u₂, u₃, u₄, u₅ u_{6 ,} u₇} { u₁, u₂, u₃, u₄, u₅ u_{6 ,} u₇},

Согласно определению в суграфе должны присутствовать все вер-шины графа G , а

{u₂, u_{6 ,}} { u₁, u₂, u₃, u₄, u₅ u_{6 ,} u₇}

Для получения подграфа из графа G были удалены вершины и с инцидентными ей ребрами u₃, u₄,_, u₇ / ■

Две вершины графа называются смежными, если они соединены

ребром (дугой).

Множество вершин, смежных с вершиной называется ее окрестностью (окрестностью единичного радиуса, сечением) и обоз-

Рис 1.9

□ Смежными с вершиной являются вершины Поэтому Г . = { } ■

Задачи для самостоятельного решения I. Задан неориентированный граф , у которого

Построить ориентированный граф, соответствующий заданному графу G .

2. Задан ориентированный граф G= < V, U >, у которого

Построить неориентированный граф, соответствующий заданному графу.

3. Является ли неориентированный граф G = <V, U > , у которого

однородным? Если да, то какой степени?

4. Является ли граф G , заданный в задаче 3, полным? Определить окрестность вершины - этого графа,

5. Задан граф G (рис.1.10). Построить часть графа, суграф, подграф

Рис.1.10

2. ВЗВЕШЕННЫЙ ГРАФ.СПОСОБЫ ЗАДАНИЯ ГРАФА.