Задача № 15.
Свободно движущаяся нерелятивистская
частица имеет относительную неопределённость
кинетической энергии порядка
.
Оцените, во сколько раз неопределённость
координаты такой частицы больше её
дебройлевской длины волны.
Решение:
Пусть
- абсолютная неопределённость кинетической
энергии. Тогда неопределённость импульса
частицы:
(1)
Воспользуемся первым соотношением неопределённостей Гейзенберга:
(2)
Найдём неопределённость координаты частицы:
(3)
Пусть кинетическая энергия частицы равняется , тогда импульс частицы . Длина волны де Бройля частицы равняется:
(4)
Найдём отношение неопределённости координаты частицы к её дебройлевской длине волны:
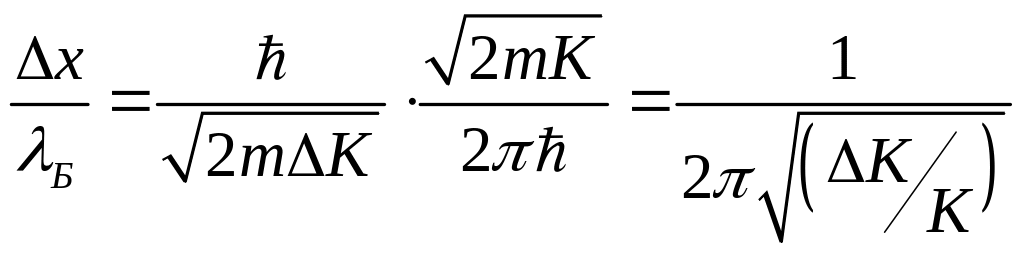(5)
Отношение
- это относительная неопределённость
кинетической энергии частицы. Таким
образом,
.
Ответ:
.
Задача № 16.
Используя соотношение неопределённостей
энергии и времени, определите естественную
ширину
спектральной линии излучения атома при
переходе его из возбуждённого состояния
в основное. Среднее время жизни атома
в возбуждённом состоянии
,
а длина волны излучения
.
Решение:
Воспользуемся соотношением неопределённостей Гейзенберга энергии и времени:
(1)
В нашем случае
- среднее время жизни атома в возбуждённом
состоянии. Поэтому неопределённость
энергии при переходе из возбуждённого
состояния в основное:
(2)
Учитывая, что
,
определим ширину спектральной линии:
(3)
Длина волны и частота излучения связаны следующим соотношением:
(4)
Продифференцируем (4) и получим следующее выражение:
(5)
Прейдём к конечным приращениям и опустим знак минус, так как он показывает только то, что при увеличении частоты длина волны излучения уменьшается, поэтому в нашем случае он не существенен:
(6)
Ответ:
.
Задача № 17.
Частица массой
движется в потенциальном поле, в котором
её потенциальная энергия равна
(гармонический осциллятор). Оцените с
помощью соотношения неопределённостей
минимально возможную энергию частицы
в этом поле.
Решение:
Энергия частицы равняется:
(1)
где
- среднее значение энергии частицы, а
- неопределённость энергии. Из выражения
(1) видно, что минимальное значение
энергии частицы, в случае
,
равняется по порядку величины её
неопределённости
.
В этом случае неопределённость импульса
частицы:
(2)
С наибольшей степенью вероятности
частица находится в области местонахождения
классического осциллятора
,
где
- амплитуда колебаний классического
осциллятора, которую определим, решая
следующее уравнение:
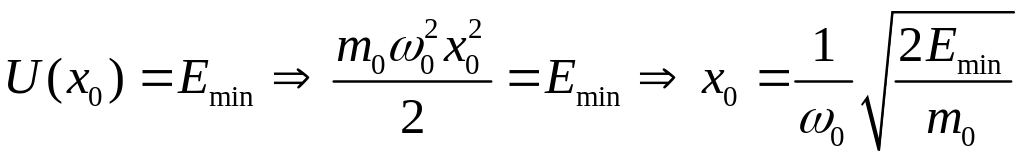(3)
где
.
Неопределённость частицы в этом
потенциальном поле
.
Воспользуемся первым соотношением
неопределённостей Гейзенберга:
(4)
Подставляя в уравнение (4) выражения, полученные для неопределённостей импульса и координаты, получим:
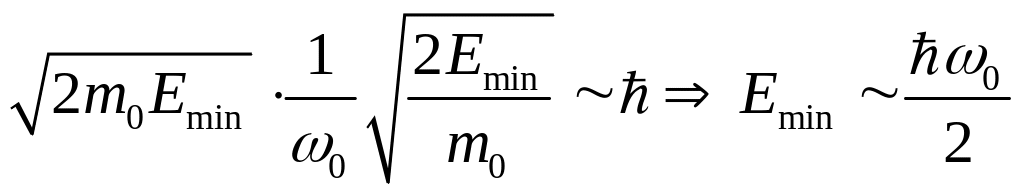(5)
Это значение соответствует нулевой энергии квантового гармонического осциллятора.
Ответ:
.