
- •Задача № 1.
- •Задача № 2.
- •Задача № 3.
- •Задача № 4.
- •Задача № 5.
- •Задача № 6.
- •Задача № 7.
- •Задача № 8.
- •Задача № 9.
- •Задача № 10.
- •Задача № 11.
- •Задача № 12.
- •Задача № 13.
- •Задача № 14.
- •Задача № 15.
- •Задача № 16.
- •Задача № 17.
- •Задача № 18.
- •Задача № 19.
- •Задача № 20.
- •Задача № 21.
- •Задача № 22.
- •Задача № 23.
- •Задача № 24.
- •Задача № 25.
- •Задача № 26.
- •Задача № 27.
- •Задача № 28.
- •Задача № 29.
- •Задача № 30.
- •Задача № 31.
- •Задача № 32.
- •Задача № 33.
- •Задача № 34.
- •Задача № 35.
- •Задача № 36.
- •Задача № 37.
- •Задача № 38.
- •Задача № 39.
- •Задача № 41.
- •Задача № 42.
- •Задача № 43.
- •Задача № 44.
- •Задача № 45.
- •Задача № 46.
- •Задача № 47.
- •Задача № 48.
- •Задача № 49.
- •Задача № 50.
- •Задача № 51.
Задача № 25.
Частица массой
находится в основном состоянии в
двумерной квадратной потенциальной
яме с бесконечно высокими стенками.
Найдите энергию частицы, если максимальное
значение плотности вероятности
местонахождения частицы равно
![]() .
.
Решение:
Частица находится в потенциальной яме, имеющей следующий вид:
Предположим, что сторона ямы равна .
Составим уравнение Шредингера для области :
(1)
или в виде:
(2)
где . Решение этого дифференциального уравнения имеет вид:
(3)
Используем естественные условия, накладываемые на пси-функцию. Вне области частица находиться не может, поэтому её пси-функция вне области равна нулю. Используя условие непрерывности, получим:
Тогда пси-функция примет вид:
(4)
Найдём вторые производные от пси-функции по x и по y:
(5)
Подставим эти производные в уравнение Шредингера (2):
(6)
Учитывая, что , получим:
(7)
Мы получили энергетический спектр частицы, находящейся в квадратной потенциальной яме с бесконечно высокими стенками. Из выражения (7) видно, что энергия частицы зависит от двух квантовых чисел и . В таблице 1 приведены несколько возможных значений и и соответствующее им , которое определяет значение энергии.
Таблица 1.
№ уровня |
|
|
|
1 |
1 |
1 |
2 |
2 |
1 |
2 |
5 |
2 |
1 |
||
3 |
2 |
2 |
8 |
Основному состоянию соответствуют значения .
Определим константу A в выражении для пси-функции (4), используя условие нормировки:
(8)
Тогда пси-функции собственных состояний имеют вид:
(9)
В основном состоянии , поэтому пси-функция имеет вид:
![]() (10)
(10)
Плотность вероятности – это квадрат модуля пси-функции:
![]() (11)
(11)
Графический вид плотности вероятности местонахождения частицы в основном состоянии представлен на рисунке 1:
Рисунок 9
Максимальное значение, которое принимает
функция синус, это единица (Как нетрудно
убедиться, координаты максимума функции
плотности вероятности равны
![]() ).
Поэтому максимальное значение плотности
вероятности:
).
Поэтому максимальное значение плотности
вероятности:
![]() (12)
(12)
Исходя из энергетического спектра частицы в квадратной потенциальной яме с бесконечно высокими стенками (7) и учитывая выражение (12), можем найти значение энергии частицы в основном состоянии :
![]() (13)
(13)
Ответ:
![]()
Задача № 26.
Частица массой находится в кубической потенциальной яме с абсолютно непроницаемыми стенками. Найдите длину ребра куба, если разность энергий 6-ого и 5-ого уровней равна . Чему равна кратность вырождения 6-ого и 5-ого уровней?
Решение:
Потенциальная яма имеет вид (рисунок 1):
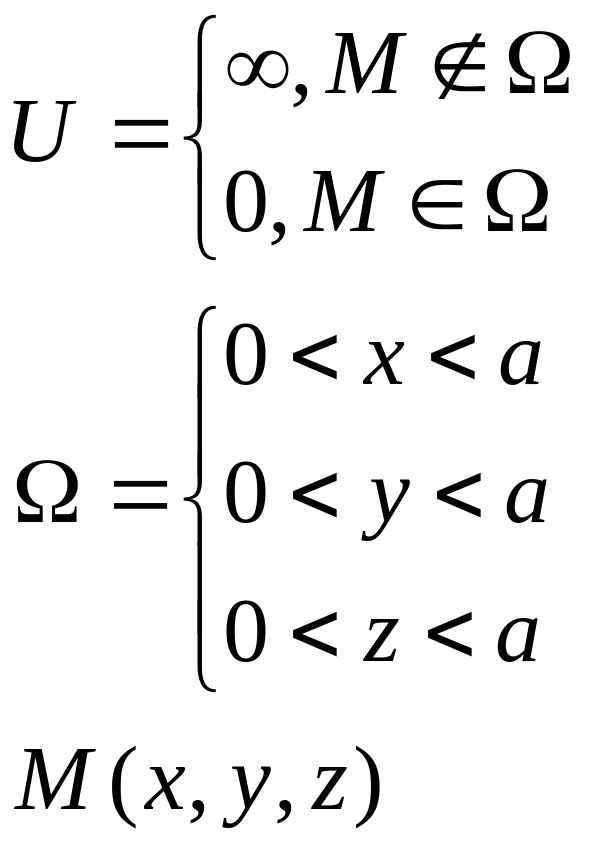
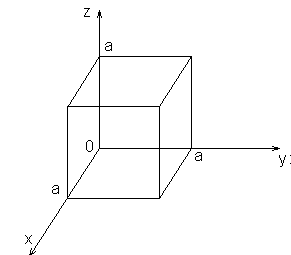
Рисунок 10
Составим уравнение Шредингера для области :
![]() (1)
(1)
или в виде:
![]() (2)
(2)
где . Решение этого дифференциального уравнения имеет вид:
![]() (3)
(3)
Используем естественные условия, накладываемые на пси-функцию. Вне области частица находиться не может, значит, плотность вероятности, а значит, и пси-функция вне области равны нулю. Учитывая этот факт и условие непрерывности пси-функций, получим:
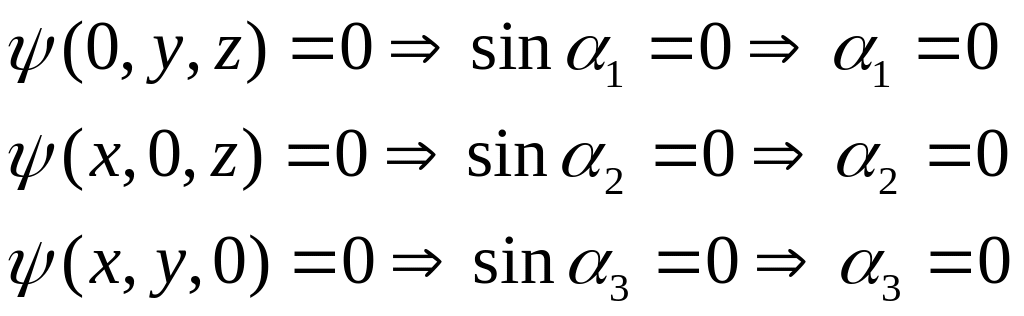
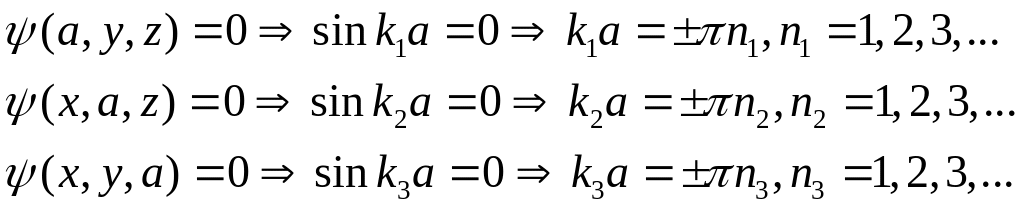
В этом случае пси-функция примет вид:
![]() (4)
(4)
Найдём частные производные от выражения (4) по x, y и z:
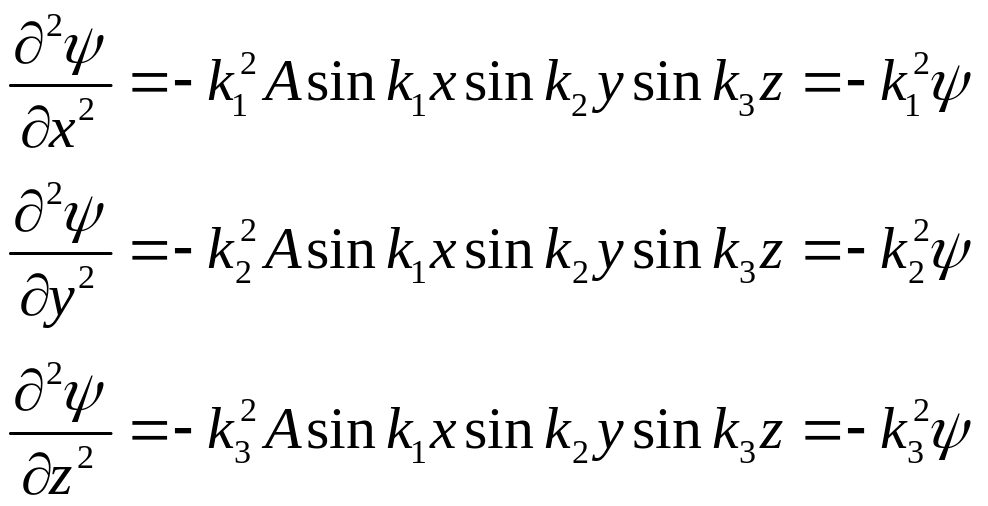
и подставим их в уравнение Шредингера (2), получим:
![]() (5)
(5)
Учитывая, что , получим:
![]() (6)
(6)
Отсюда получим энергетический спектр частицы:
![]() (7)
(7)
Энергия частицы зависит от трёх квантовых
чисел
![]() .
Составим таблицу (таблица 1), в которой
рассмотрим несколько первых энергетических
уровней (сумма квадратов трёх квантовых
чисел
.
Составим таблицу (таблица 1), в которой
рассмотрим несколько первых энергетических
уровней (сумма квадратов трёх квантовых
чисел
![]() определяет энергию частицы):
определяет энергию частицы):
Таблица 1:
№ уровня |
|
|
|
|
1 |
1 |
1 |
1 |
3 |
2 |
1 |
1 |
2 |
6 |
1 |
2 |
1 |
||
2 |
1 |
1 |
||
3 |
1 |
2 |
2 |
9 |
2 |
1 |
2 |
||
2 |
2 |
1 |
||
4 |
1 |
1 |
3 |
11 |
1 |
3 |
1 |
||
3 |
1 |
1 |
||
5 |
2 |
2 |
2 |
12 |
6 |
1 |
2 |
3 |
14 |
1 |
3 |
2 |
||
2 |
1 |
3 |
||
2 |
3 |
1 |
||
3 |
1 |
2 |
||
3 |
2 |
1 |
Как видно из таблицы, может существовать несколько состояний частицы, описываемых различными пси-функциями, но в которых частица имеет одно и то же значение энергии. Такие энергетические уровни называются вырожденными, а число квантовых состояний, в которых частица имеет одно и тоже значение энергии называется кратностью вырождения. Значит, 5-ый энергетический уровень не вырожден, потому что существует только одно состояние, в котором частица имеет такое значение энергии, а 6-ой уровень имеет кратность вырождения 6. Определим разность энергий 6-ого и 5-ого уровней:
![]() (8)
(8)
Отсюда найдём ребро куба:
![]() (9)
(9)
Ответ:
5-ый уровень не вырожден, кратность вырождения 6-ого уровня равна 6.
