
- •Ен. Ф. 01 математика Методические указания и варианты заданий к контрольной работе № 1
- •280402 Природоохранное обустройство территорий
- •Введение
- •Примеры решения задач Задача 1
- •Метод Гаусса
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Расчетные задания Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •Библиографический список
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Кафедра математики
Ен. Ф. 01 математика Методические указания и варианты заданий к контрольной работе № 1
Специальности: 250201 Лесное хозяйство
280402 Природоохранное обустройство территорий
Уфа 2009
УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией факультета лесного хозяйства (протокол № 6 от 24.04.2009 года)
Составители: доцент, к.соц.н. Саитова Р.З.
доцент, к.физ.-мат.н. Маннанов М.М.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент, к.физ.-мат.н. Лукманов Р.Л.
Введение
Целью настоящих методических указаний является помощь студентам в освоении и закреплении следующих разделов математики: линейная и векторная алгебра, аналитическая геометрия.
Расчетно-графическая работа № 1 состоит из 5 заданий. В каждом задании 30 вариантов. Номер варианта студент выбирает по формуле: № = a · b + c, где a – номер задания, b и с – предпоследняя и последняя цифры шифра (номера зачетной книжки или студенческого билета).
Например, номер студенческого билета (зачетки) студента 1265. Тогда в первом задании этот студент выполняет вариант: № = 1 · 6 + 5 = 11. Во втором задании: № = 2 · 6 + 5 = 17 и т.д. Если получается вариант больше 30, то нужно вычитать 30. Например, для этого же студента третье задание будет высчитываться: 5 · 6 + 5 = 35. Следовательно, этот студент решает 35 – 30 = 5 – пятый вариант третьего задания.
Прежде чем приступать к выполнению работы, целесообразно изучить соответствующие разделы в учебниках, рекомендованных в библиографическом списке.
Примеры решения задач Задача 1
1-й способ решения
Пусть требуется, используя формулы Крамера, решить систему
![]()
Подсчитаем сначала главный определитель системы ∆, воспользовавшись следующим правилом вычисления определителей третьего порядка:
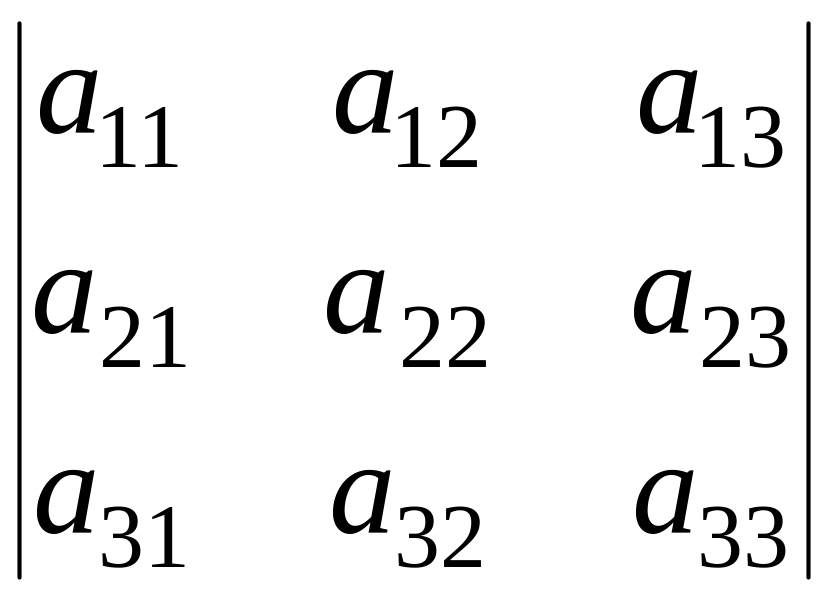 =
а11
·
=
а11
·
![]() –
а12
·
–
а12
·
![]() +
а13
·
+
а13
·
![]() .
.
У
нас
∆
=
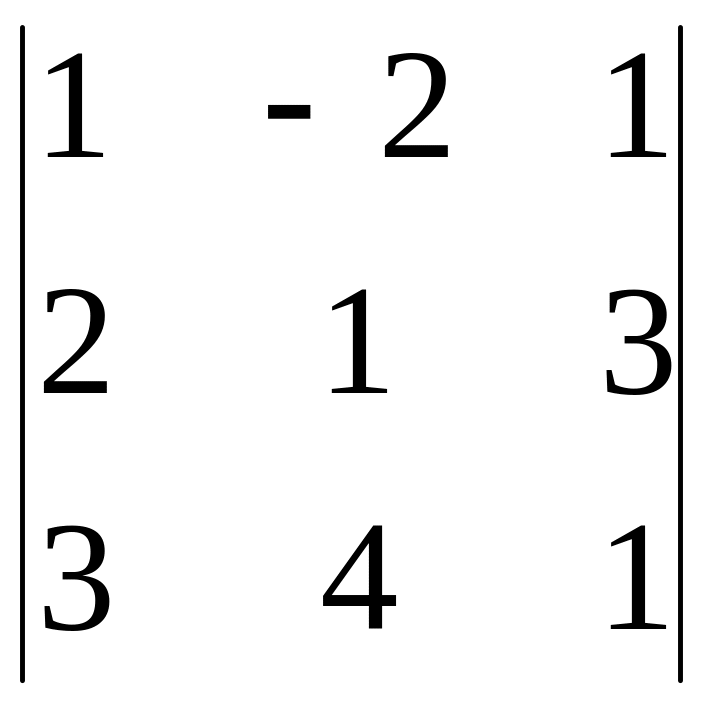 =
1
∙
(1
–
12)
+
2
∙
(2
–
9)
+
1
∙
(8
–
3)
=
–
20.
=
1
∙
(1
–
12)
+
2
∙
(2
–
9)
+
1
∙
(8
–
3)
=
–
20.
Так как ∆ ≠ 0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители ∆x, ∆y, ∆z:
∆x
=
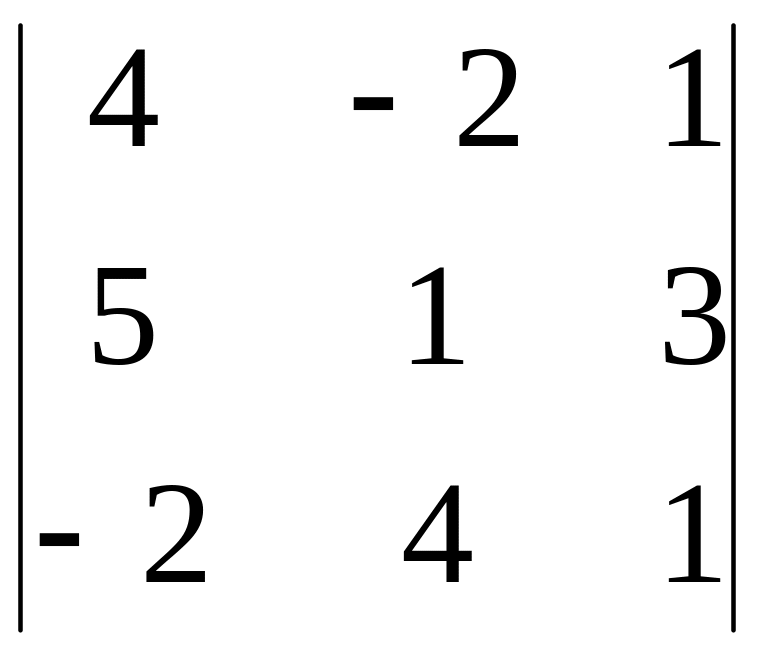 =
4
·
(1
–
12)
–
(–
2)
·
(5
+
6)
+
1
·
(20
+
2)
=
0,
=
4
·
(1
–
12)
–
(–
2)
·
(5
+
6)
+
1
·
(20
+
2)
=
0,
∆y
=
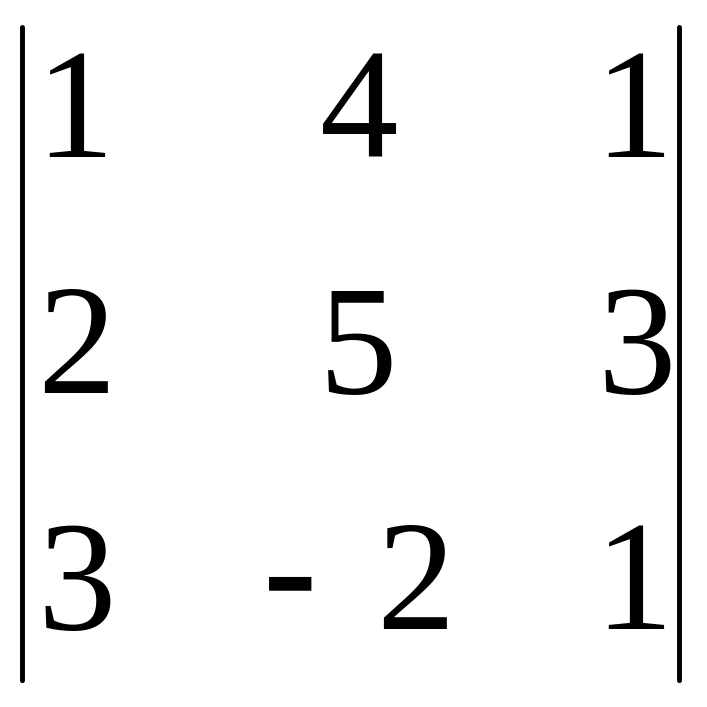 =
1
·
(5
+
6)
–
4
·
(2
–
9)
+
1
·
(–
4
–
15)
=
20,
=
1
·
(5
+
6)
–
4
·
(2
–
9)
+
1
·
(–
4
–
15)
=
20,
∆z
=
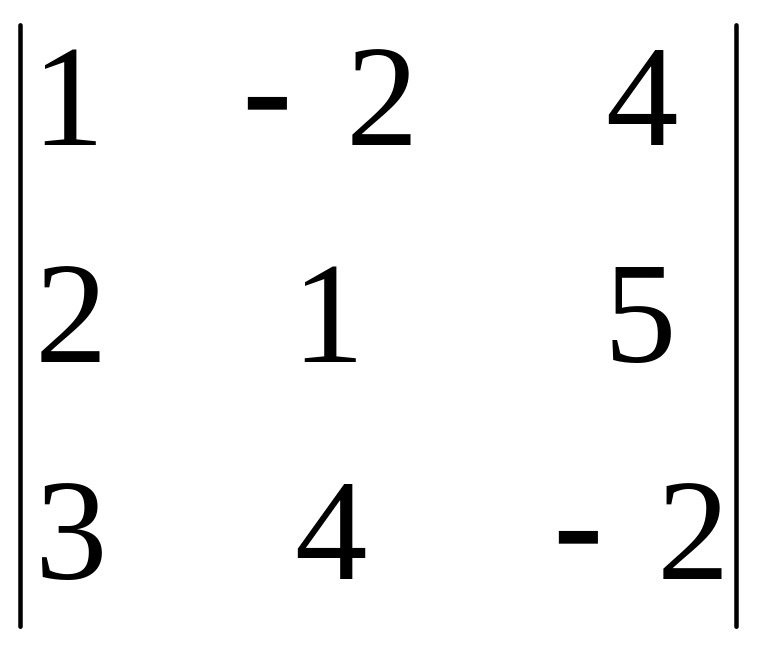 =
1
·
(–
2
–
20)
–
(–
2)
·
(–
4
–
15)
+
4
·
(8
–
3)
=
–
40.
=
1
·
(–
2
–
20)
–
(–
2)
·
(–
4
–
15)
+
4
·
(8
–
3)
=
–
40.
Далее, воспользовавшись формулами Крамера, окончательно получим
x
=
![]() =
0,
y
=
=
0,
y
=
![]() =
–
1,
z
=
=
–
1,
z
=
![]() =
2.
=
2.
Всем трем равенствам они удовлетворяют, поэтому делаем вывод о правильности полученного решения: x = 0; y = – 1; z = 2.
2-й способ решения
Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:
![]()
Решение. Обозначим через А – матрицу коэффициентов при неизвестных; Х – матрицу-столбец неизвестных x, y, z и Н – матрицу-столбец свободных членов:
А
=
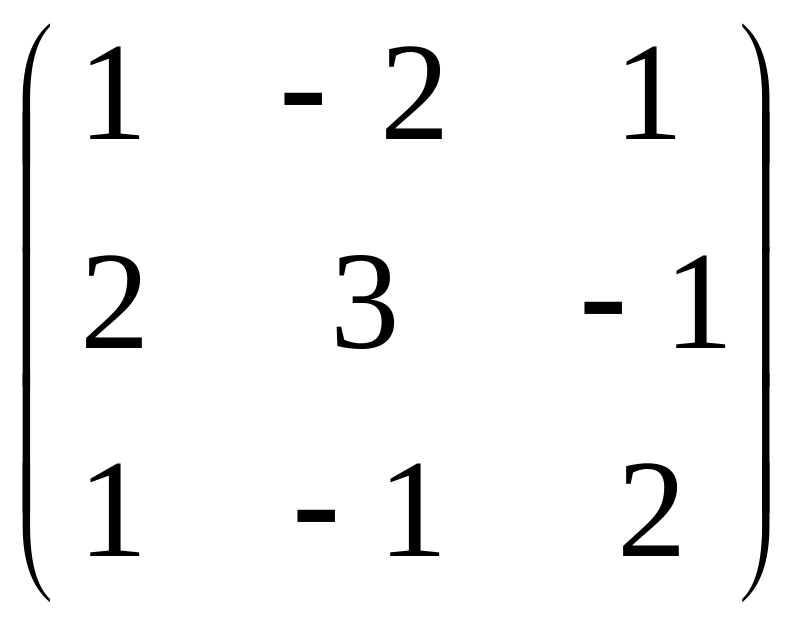 ,
Х
=
,
Х
=
![]() ,
Н
=
,
Н
=
![]() .
.
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
А · Х = Н. (1)
Если матрица А – невырожденная (ее определитель ∆ отличен от нуля), то она имеет обратную матрицу А–1. Умножив обе части уравнения (1) на А–1 слева, получим:
А–1 · А · Х = А–1 · Н.
Но А–1 · А = Е (Е – единичная матрица), а ЕХ = Х, поэтому
Х = А–1 · Н. (2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А–1.
Пусть имеем невырожденную матрицу
А
=
![]() .
Тогда
А–1
=
.
Тогда
А–1
=
 ,
,
где Аij (i = 1, 2, 3; j = 1, 2, 3) – алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (– 1)i+j на минор (определитель) второго порядка, полученный вычеркиванием i-й строки j-го столбца в определителе матрицы А, т.е. Aij = (– 1)i+j · Mij.
Вычислим определитель ∆ и алгебраические дополнения Аij элементов матрицы А.
∆ =
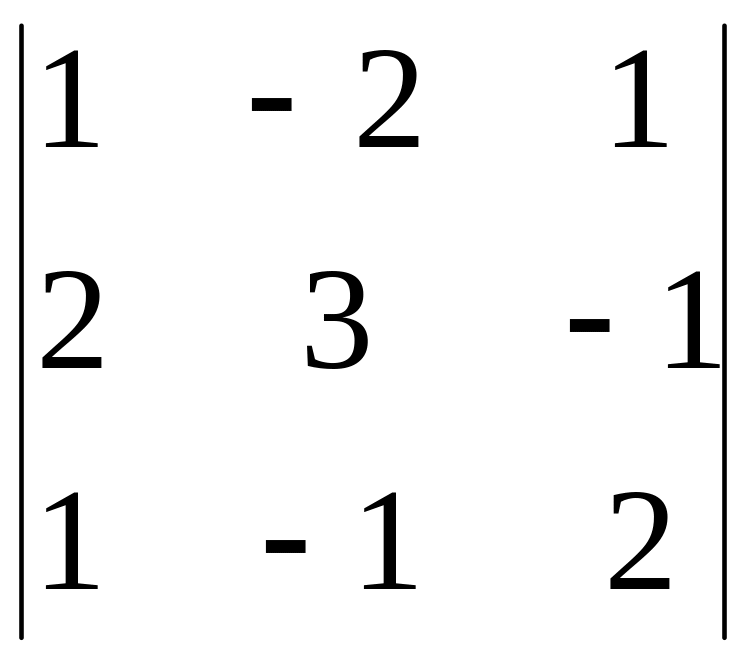 =
10
≠
0,
следовательно,
матрица
А
имеет
обратную
матрицу
А–1.
=
10
≠
0,
следовательно,
матрица
А
имеет
обратную
матрицу
А–1.
А11
=
(–
1)1+1
∙
![]() =
5, А21
=
(–
1)2+1
∙
=
5, А21
=
(–
1)2+1
∙
![]() =
3,
=
3,
А12
=
(–
1)1+2
∙![]() =
–
5, А22
=
(–
1)2+2
∙
=
–
5, А22
=
(–
1)2+2
∙
![]() =
1,
=
1,
А13
=
(–
1)1+3
∙
![]() =
–
5, А23
=
(–
1)2+3
∙
=
–
5, А23
=
(–
1)2+3
∙
![]() =
–
1,
=
–
1,
А31
=
(–
1)3+1
∙
![]() =
–
1, А32
=
(–
1)3+2
∙
=
–
1, А32
=
(–
1)3+2
∙
![]() =
3,
=
3,
А33
=
(–
1)3+3
∙
![]() =
7.
=
7.
Тогда
А–1
=
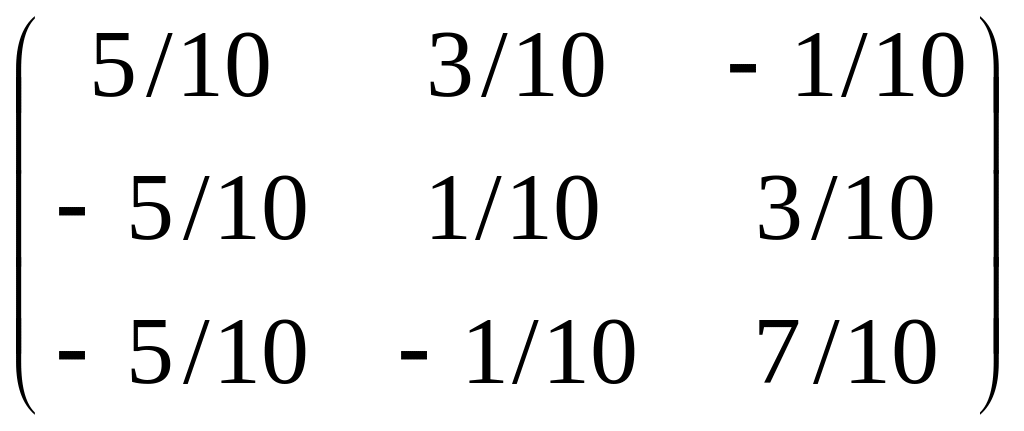 =
=
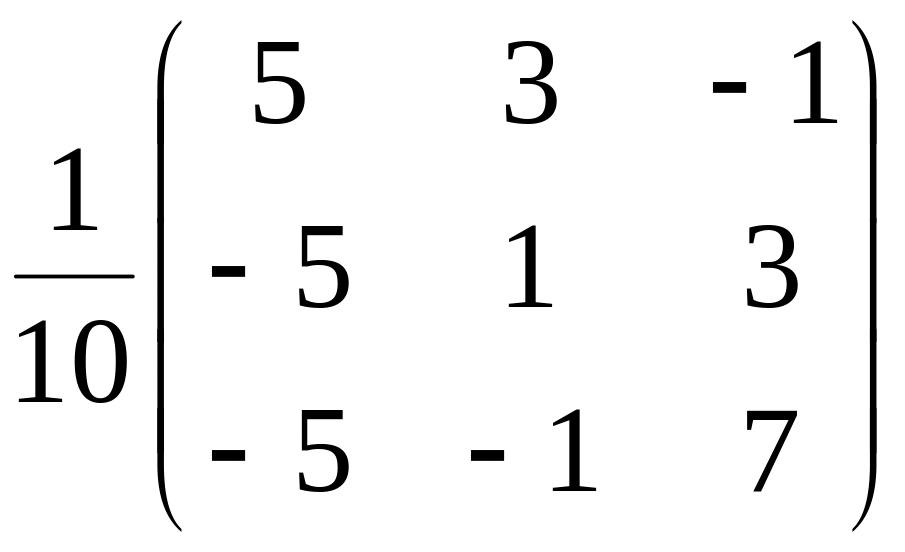 .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:
Х
=
А–1
·
Н
=
![]() ·
·
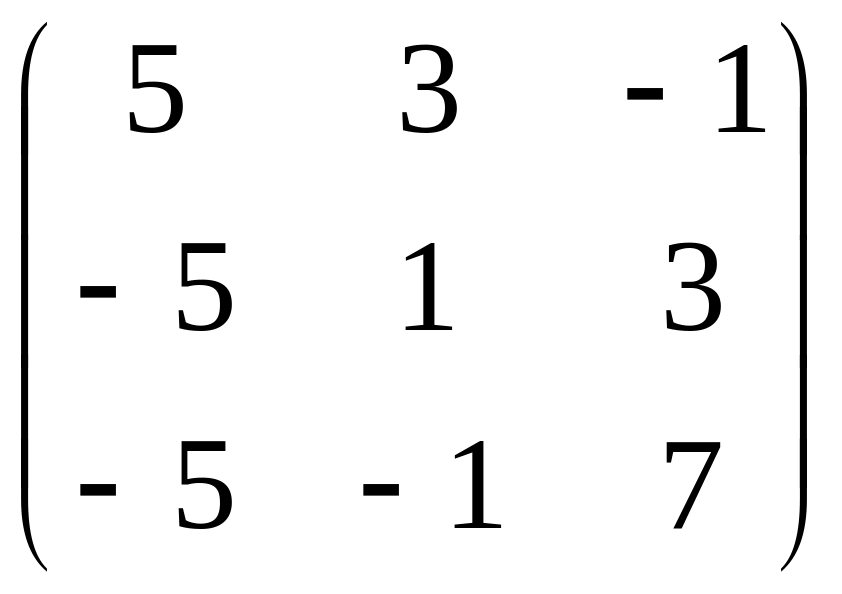 ·
·
![]() =
=
=
=
![]() ·
·
![]() =
·
=
·
![]() =
=
![]() .
.
Отсюда x = 3, y = 0, z = – 2.
3-й способ решения

