2. Расчет переходного процесса

Переходный процесс в объекте регулирования будем рассчитывать по решению (11) уравнения (10). Чтобы выполнить этот расчет необходимо сначала определить постоянную времени, Т, и коэффициент усиления, k. Будем для этого использовать следующие функции:

момент турбины

момент компрессора

производная от момента турбины по частоте вращения

производная от момента турбины по расходу топлива

,

где, G_T= G_T/G_Tmax; n_T=0,75; C_T=17500; n_K=1,5; C_K=14000; _max=1466,08.

Задание для самостоятельной работы.

1. Рассчитать постоянные времени и коэффициенты усиления по расходу топлива для трех режимов работы двигателя при =_max, G_T= 1; =1361,36, G_T=0,918 =1256,64, G_T=0,864. Выбрать для расчета одно из значений момента инерции J=25, 30, 35.

2. Рассчитать кривые переходных процессов при полученных значениях T и k. Диапазон изменения времени выбрать от 0 до t3T.

3. Сделать выводы по работе, в которых отобразить влияние режима работы на величину постоянной времени, влияние постоянной времени на длительность переходного процесса. Объяснить полученные кривые переходных процессов.

Лабораторная работа № 3 Исследование частотных характеристик типовых звеньев сар

Цель работы. Рассчитать, построить графически и проанализировать амплитудно-частотные (АЧХ), фазочастотные (ФЧХ) и амплитудно-фазовые характеристики следующих звеньев: апериодического , инерционного интегрирующего и инерционного дифференцирующего.

Теоретические основы

1. Апериодическое звено I порядка. В качестве примеров апериодических звеньев I порядка можно привести ротор ГТД, печь, резервуар с газом, RC-цепочку др.

Математической моделью апериодического звена I порядка является обыкновенное линейное дифференциальное уравнение I порядка

,

где Т – постоянная времени, k – коэффициент усиления.

Применяя преобразование Лапласа к этому уравнению, получим передаточную функцию

.

Производя замену р=i получим частотную функцию

.

Выделим вещественную и мнимую части частотной функции

, .

Определим модуль и аргумент частотной функции апериодического звена I порядка

Амплитудно-частотной характеристикой называется зависимость модуля частотной функции от частоты, а фазочастотной – зависимость аргумента частотной функции от частоты.

Для апериодического звена I порядка частотные характеристики можно построить приближенно, используя упрощенные выражения частотной частотной функции в областях малых и больших частот. Областью низких частот будем считать область <<_ср, а высоких частот область >>_ср, где _ср=1/Т. Параметр _ср называется частотой среза.

В области низких частот ²Т²<<1, поэтому |K|k, а в области высоких частот ²Т²>>1, следовательно

Таким образом, в области низких частот модуль частотной функции есть величина постоянная, а в высоких частот представляет собой гиперболу. При =_ср |K|=k/2.

Аргумент частотной функции в области низких частот Arg(K)=-arctg(Т)-Т=-Const, а в области высоких частот при  Arg(K)-/2. При =_ср Arg(K)=-/4.

АЧХ часто строят в логарифмических координатах. Это позволяет охватить на одном графике диапазон изменения модуля частотной функции в несколько порядков. Для того, чтобы получить АЧХ в шкале децибел используют следующую формулу

Для логарифмической АЧХ также можно получить приближенные выражения для областей низких и высоких частот

при <<_ср А()|20lgk, так как lg(1+²T²)lg(1)=0

при >>_ср А()|20lgk – 20lg(T)=20lg(k/T) – 20lg, так как ²Т²>>1.

Логарифмические АЧХ и ФЧХ апериодического звена I порядка приведены на рис.1

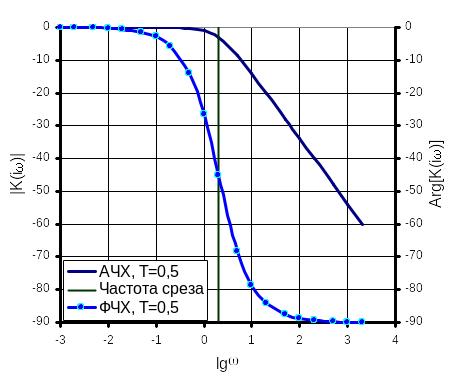
Рис.1. Апериодическое звено I порядка

Из приведенной характеристики следует, что в области низких частот апериодическое звено I порядка пропускает гармонические сигналы с постоянным усилением, не зависящим от частоты. Фазовое запаздывание на низких частотах близко к 0. В области частот, близких к частоте среза фазовое запаздывание в апериодическом звене I порядка резко возрастает, а также с ростом частоты значительно увеличивается ослабление выходного сигнала при постоянной амплитуде входного: 10-кратному увеличению частоты соответствует 10-кратное ослабление выходного сигнала.

2. Интегрирующие звенья. В качестве примеров интегрирующих звеньев можно привести гидропривод, двигатель постоянного тока и др.

Динамические процессы интегрирующих звеньев описываются дифференциальными уравнениями

– идеальное интегрирующее,

– инерционное интегрирующее,

где Т – постоянная времени, k – коэффициент усиления.

Передаточная функция инерционного интегрирующего звена

представляет собой произведение передаточных функций апериодического звена I порядка w_ап=k/(Tp+1) и идеального интегрирующего звена w_ид.инт=1/р, с коэффициентом усиления k_идинт=1. Такая передаточная функция соответствует системе, состоящей из двух последовательно включенных звеньев – апериодического I порядка и идеального интегрирующего.

Модуль частотной функции системы, состоящей из двух последовательно включенных звеньев, представляет собой произведение модулей частотных функций звеньев, а аргумент – сумму аргументов. Так как модуль частотной функции идеального интегрирующего звена с коэффициентом усиления k_идинт=1 есть K(i)=1/, то модуль частотной функции инерционного интегрирующего звена будет

.

Так как аргумент частотной функции апериодического звена I порядка есть –arctg(T), а идеального интегрирующего звена –/2 то для инерционного интегрирующего звена получим

Arg(K_ин.инт.) = Arg(K_ид.инт) + Arg(K_ап) = –/2 – arctg(T)

При построении частотных характеристик инерционного интегрирующего звена можно также, как это было сделано для апериодического звена I порядка, использовать приближение низких и высоких частот. В области низких частот, при <<_ср, K_ининтk/, так как ²Т²<<1, а ; для логарифмической АЧХ получим A()=20lg(k/) = 20lgk – 20lg; Arg(K) –/2 – T, так как arctg(T)T. В области высоких частот, при >>_ср, K_ин.интk/²T=Const/², так как ²Т²>>1, ; для логарифмической АЧХ A()=20lg(k/²T) = 20lg(k/T) – 40lg; Arg(K) –, поскольку при  arctg(T)–/2.

Частотные характеристики инерционного интегрирующего звена приведены на рис.2.

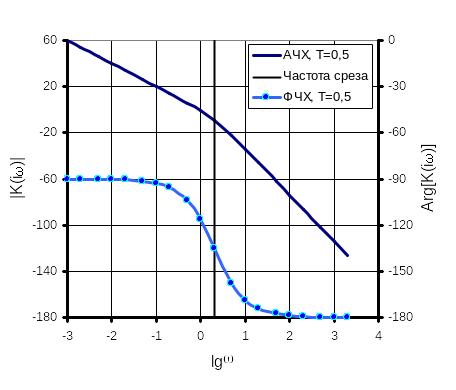
Рис.2. Инерционное интегрирующее звено

Из характеристик рис.2 следует, что в низкочастотной области частотные характеристики инерционного интегрирующего звена совпадают с характеристиками идеального интегрирующего звена. Инерционные свойства этого звена начинают проявляться в окрестности частоты среза, где значительно увеличивается фазовое запаздывание, а темп затухания изменяется от 20 дБ/дек до 40 дБ/дек.

3. Дифференцирующие звенья. Динамические процессы в дифференцирующих звеньях описываются дифференциальными уравнениями

– идеальное дифференцирующее,

– инерционное дифференцирующее,

где Т – постоянная времени, k – коэффициент усиления.

Передаточная функция инерционного дифференцирующего звена

представляет собой произведение передаточных функций апериодического звена I порядка w_ап=k/(Tp+1) и идеального дифференцирующего звена w_ид.диф=р, с коэффициентом усиления k_иддиф=1. Такая передаточная функция соответствует системе, состоящей из двух последовательно включенных звеньев – апериодического I порядка и идеального дифференцирующего.

Так как модуль частотной функции идеального дифференцирующего звена с коэффициентом усиления k_идинт=1 есть K(i)=, то модуль частотной функции инерционного дифференцирующего звена будет

.

Аргумент частотной функции апериодического звена I порядка есть –arctg(T), а идеального дифференцирующего звена /2, поэтому, для инерционного дифференцирующего звена получим

Arg(K_ин.диф.) = Arg(K_ид.диф) + Arg(K_ап) = /2 – arctg(T)

Построим частотные характеристики инерционного дифференцирующего звена, используя приближение низких и высоких частот. В области низких частот, при <<_ср, K_ининтk, так как ²Т²<<1, ; для логарифмической АЧХ получим A()=20lg(k/) = 20lgk – 20lg; Arg(K) –/2 – T, так как arctg(T)T. В области высоких частот область при >>_ср, K_ининтk/²T=Const/², так как ²Т²>>1, ; для логарифмической АЧХ A()=20lg(k/²T) = 20lg(k/T) – 40lg; Arg(K) –, поскольку при  arctg(T) –/2.

Частотные характеристики инерционного дифференцирующего звена приведены на рис.2. Из характеристик следует, что в низкочастотной области инерционность инерционного дифференцирующего звена практически не проявляется, так как его характеристики совпадают с характеристиками идеального дифференцирующего звена. В высокочастотной области фазовое опережение инерционного дифференцирующего звена стремится к 0, а коэффициент усиления становится постоянным, не зависящим от частоты, а это означает, что в области высоких частот инерционное дифференцирующее звено вырождается в безынерционное усилительное звено.

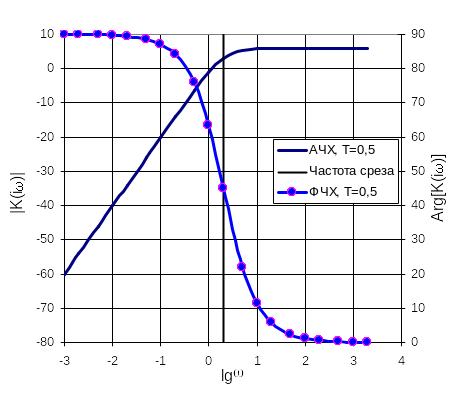
Рис.3. Инерционное дифференцирующее звено

Задание на лабораторную работу

1). Рассчитать и построить логарифмические АЧХ и ФЧХ апериодического звена I порядка, инерционного интегрирующего и инерционного дифференцирующего звеньев.

2). Проанализировать построенные характеристики и сделать выводы, в которых отразить поведение частотных характеристик в областях низких и высоких частот: темп затухания, фазовое запаздывание (опережение) и другие особенности.