19

Лабораторная работа №1 Исследование динамических свойств объекта регулирования.

Цель работы. Ознакомится с методом линеаризации уравнения динамики объекта регулирования (ОР). Рассчитать постоянную времени ОР и коэффициент усиления по расходу топлива. Построить кривую переходного процесса ОР.

1.Теоретическая часть

Авиационный газотурбинный двигатель в процессе полета работает на различных режимах – взлетном, номинальном, крейсерском и др. Процесс перехода с одного режима на другой есть процесс неустановившийся (переходный). Поведение двигателя на переходных режимах определяется собственными динамическими свойствами двигателя.

Для того, чтобы проанализировать динамические свойства ГТД запишем уравнение динамики ротора одновального ТРД

(1)

Это уравнение представляет собой II закон Ньютона для вращающихся тел. В этом уравнении J=r²dm [кгм²], момент инерции ротора, где dm – элемент массы ротора, r – расстояние от этого элемента, до оси вращения ротора;  – круговая частота вращения ротора,  =2n/60, где n – число оборотов ротора в минуту. Производная представляет собой угловое ускорение ротора. М_Т и М_К – моменты турбины и компрессора. Их также называют: М_Т – крутящий момент, М_К – момент сопротивления.

На установившемся режиме М_Т0 = М_К0 (индексом 0 будем обозначать параметры на установившимся режиме), следовательно угловое ускорение , ротор вращается с постоянной частотой вращения . Если М_Т > М_К, ротор разгоняется, М_Т < М_К, ротор тормозится. Процессы разгона и торможения описываются уравнением (1). Однако это уравнение нелинейно, поскольку М_Т, М_К являются нелинейными функциями . Решать нелинейное уравнение сложно, а во многих случаях, возможно получить только приближенное или численное (тоже приближенное) решение. Поэтому упростим уравнение (1), выполнив его линеаризацию.

Рассмотрим зависимости момента турбины от  при Т_г=Const и момента компрессора от , представленные на рис.1. Будем полагать, что

М_т= М_т(G_т ,), М_к= М_к();

При малых отклонениях от стационарного режима  =  – ₀ , причем /₀<<1 (условие малости отклонений)

M_т =M_т0+_т; M_к =M_к0+_к;

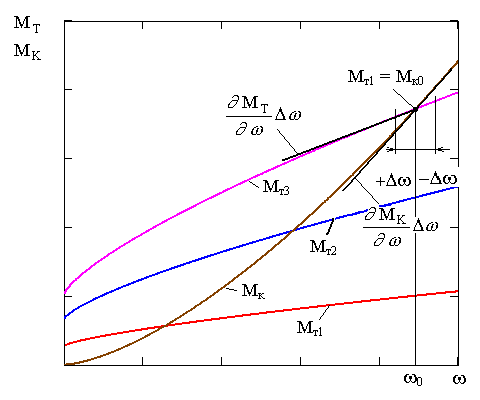
Рис.1. Зависимость M_т и M_к от частоты вращения

Так как М_Т0 = М_К0, то M_т  M_к=_тМ_к; кроме того d=d(₀+)=d. Подставляя полученные выражения для M_т  M_к и d в (1) получим уравнение динамики ротора, записанное относительно отклонений

Jd/dt=_тМ_к (2)

При малых отклонения от стационарного режима касательные к кривым M_т и M_к будут с достаточной точностью заменять сами кривые. Погрешность такой замены будет тем больше, чем больше будет отклонение от стационарного режима . Для того, чтобы заменить M_т и M_к касательными разложим эти функции в ряд Тэйлора, ограничиваясь при этом членом порядка не выше 

(3)

(4)

Полученные разложения являются линейными функциями, G_т ,  в малой окрестности стационарного режима. Подставляя (3), (4) в уравнение (2) и проводя преобразования, получим уравнение

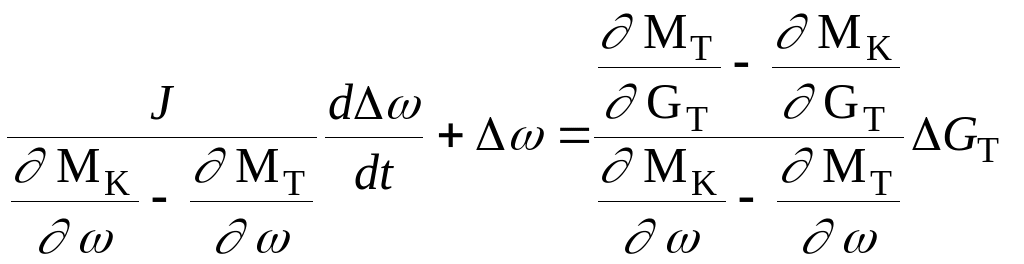(5)

Введем обозначения

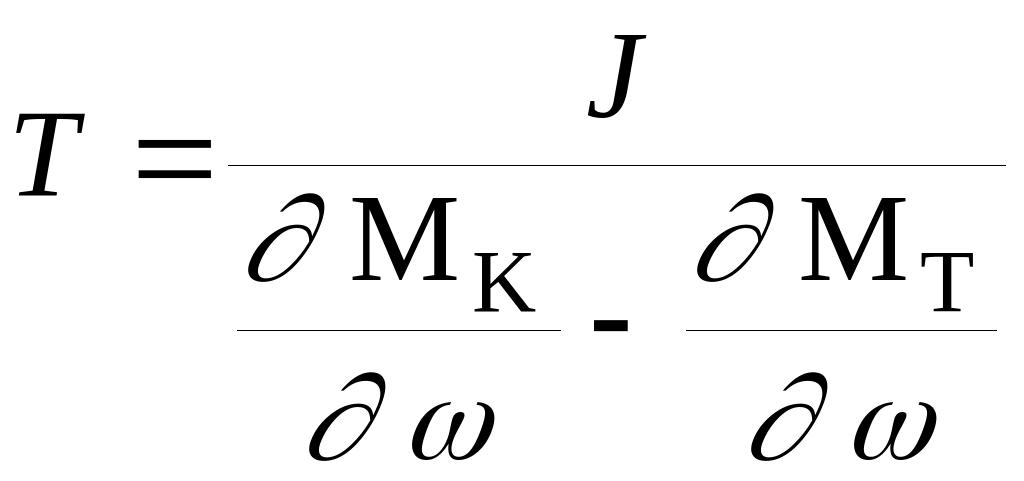, (6)

(7)

с учетом которых уравнение (5) примет вид

(8)

Мы получили линейное неоднородное ОДУ первого порядка, где искомой функцией является  (отклонение частоты вращения ротора). Входящие в это уравнение коэффициенты в теории автоматического регулирования называются так:

T - имеет размерность сек и называется постоянной времени; постоянная времени определяет инерционность объекта регулирования. Обычно ГТД имеют постоянную времени в пределах 5...10 с.

k_G - коэффициент передачи или коэффициент усиления по расходу топлива влияние G_T на .

Перейдем в уравнении (9) к безразмерным параметрам и . Уравнение в этом случае примет вид

Ty’+ y = kx (10)

где 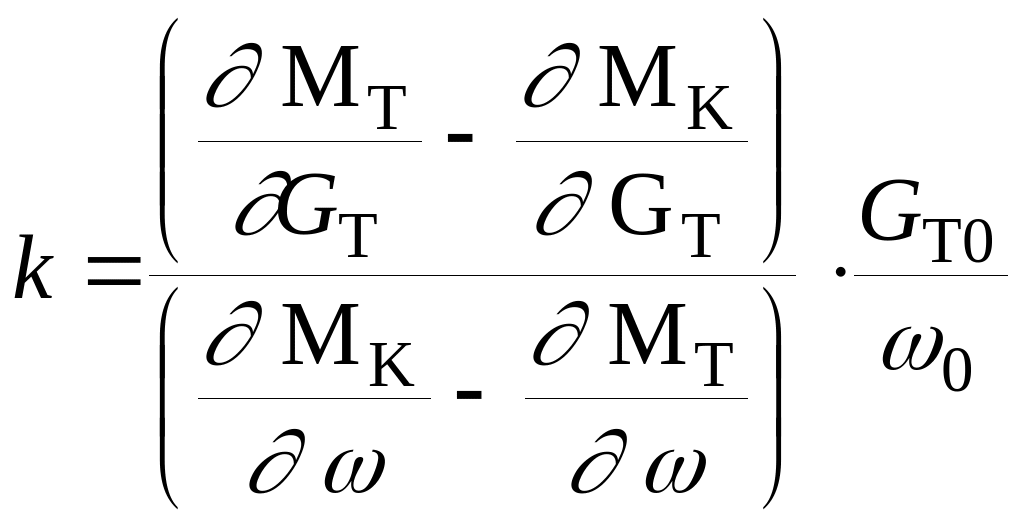– коэффициент усиления

В уравнении (10) y – выходной сигнал (выходной параметр, регулируемый параметр), x – входной сигнал (входной параметр, управляющее воздействие).

Проведем теперь исследование переходного процесса в ГТД. Определим, как будет изменяться выходной сигнал при изменении входного сигнала. Для этого нужно решить уравнение (10). Будем искать решение для скачкообразного изменения входного сигнала x(t) = x₀1(t), где 1(t) – функция Хевисайда, которая обладает следующими свойствами

0 при t<0

1(t) = 

1 при t0

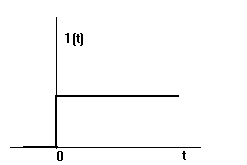
Рис.2. Скачкообразная функция (функция Хевисайда)

Общее решение линейного неоднородного ОДУ представляет собой сумму двух решений

у = у_ооду + у_чнду ,

где, у_ооду – общее решение однородного ОДУ, у_чнду – частное решение неоднородного ОДУ.

Общим решением однородного уравнения Ту’+y=0 будет функция

у_ооду = Ae^t/T

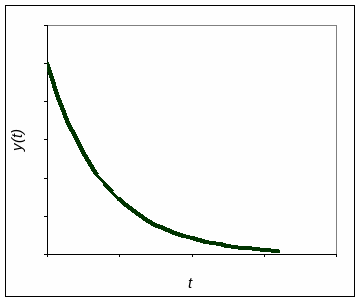
Рис.3. Общее решение однородного ОДУ

Общее решение однородного уравнения описывает свободное движение системы, т.е. движение, когда система была выведена из равновесия и возвращается в равновесие без воздействия внешних сил.

Частное решение неоднородного ДУ найдем таким образом, чтобы оно удовлетворяло стационарному решению, т.е. y(t)

у_чнду = kx

Тогда общее решение НДУ

у_онду = kx + Ae^-t/T ;

Определим константу интегрирования А, используя начальное условие

y=0 при t<0. Тогда 0=kx+Ae^-0/T, откуда A= – kx и окончательно общее решение неоднородного ОДУ принимает вид

y=kx(1 – e ^{– t/T}); (11)

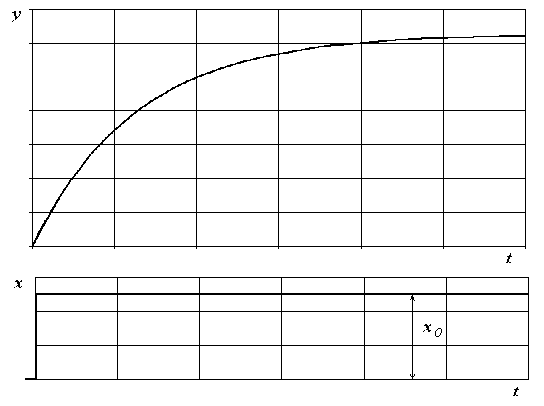
Рис.3. Переходный процесс при скачкообразном входном сигнале

Это решение определяет так называемую переходную функцию а –решение дифференциального уравнения. при скачкообразном входном сигнале.

Постоянная времени характеризует инерционность объекта, т.е. время его перехода с одного установившегося режима на другой. Чем меньше постоянная времени, тем быстрее протекает переходный процесс. Определим время, в течение которого выходной сигнал достигает 95% от стационарного значения 0,95у_устk(1 – e^{-– 3})=k(1–exp(–3T/T)). Если положить, что переходный процесс практически заканчивается по достижении выходным сигналом значения составляющего 95% от стационарного, то можно сказать, что длительность переходного процесса t_п  3Т.

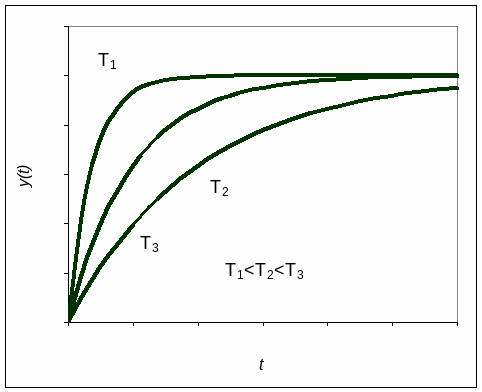
Рис.4. Переходные процессы при различных постоянных времени.