Системы с фиксированным количеством вещества

При моделировании динамики численности видов в замкнутых экосистемах продуктивным оказался подход, когда переменными, входящими в уравнения, являются не биомассы видов, а общие массы того или иного вещества, содержащегося в организмах каждого вида. Такой подход, позволяющий учесть замкнутость системы по массе, впервые предложен В.В. Алексеевым в 1976, и в настоящее время широко используется в имитационном моделировании конкретных экосистем.

Рассмотрим циркуляции вещества в системе, состоящей из растений-продуцентов (M₁⁽ⁱ⁾), опада (М₂⁽ⁱ⁾), редуцентов (М₃⁽ⁱ⁾), минерализующих спад, и почвы (М_п) (рис. 10.9). Перечеркнутыми стрелками обозначены потоки вещества, определяемые процессом отмирания живых организмов. Скорости этих процессов считаются пропорциональными биомассе соответствующих видов (линейные члены в уравнениях). Простыми стрелками обозначены потоки вещества, обусловленные активными взаимодействиями живых организмов друг с другом и с неживым веществом. Скорости таких потоков, следуя Вольтерра, пропорциональны вероятности встречи особей разных видов друг с другом, т. е. произведению масс вещества, заключенного в каждом из взаимодействующих блоков системы (билинейные члены в уравнениях).

Резервуар минеральных питательных веществ М_п будет общим для п трофических пирамид, причем между видами на разных трофических уровнях могут осуществляться всевозможные взаимодействия. Чтобы не загромождать схему, на рис. 10.10 указаны лишь некоторые из потоков вещества между компонентами системы.

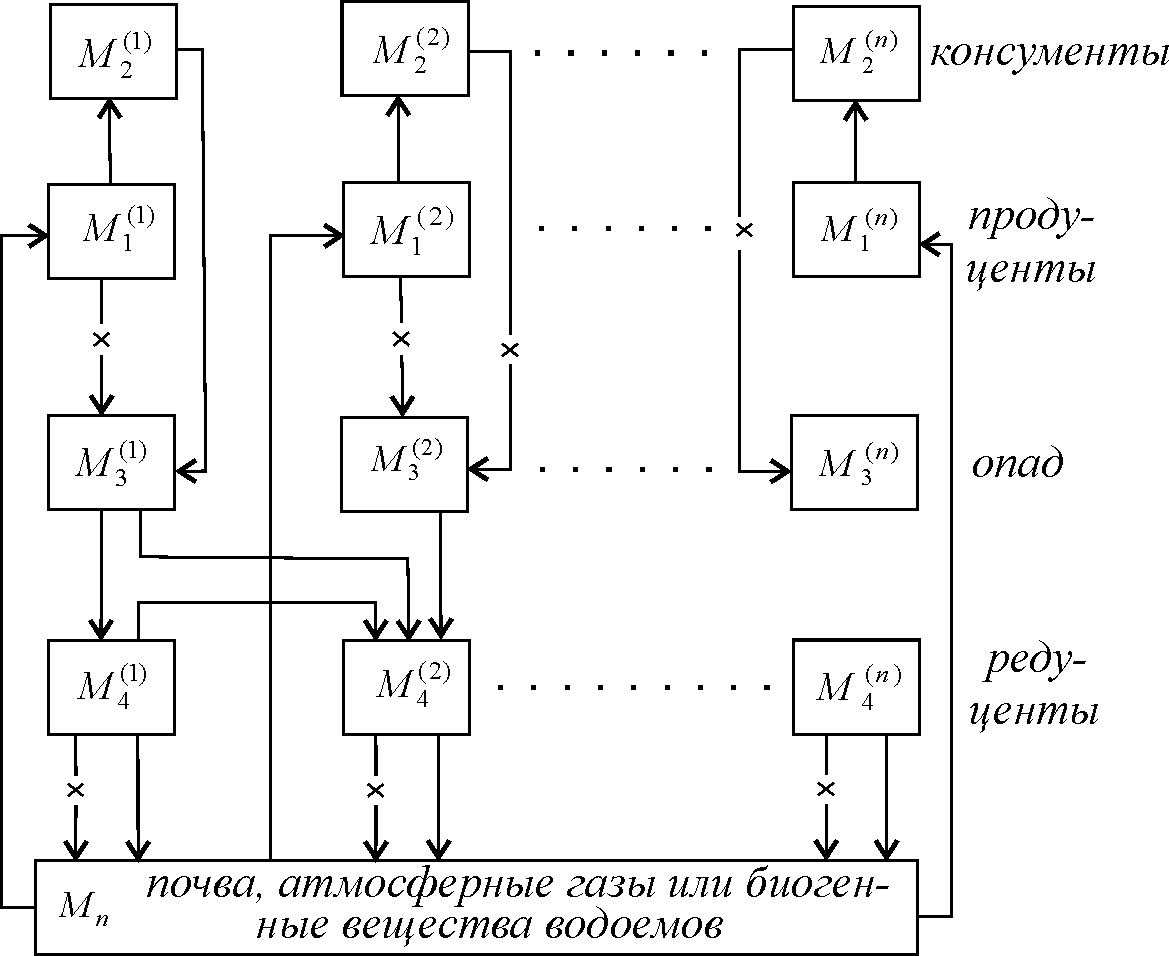
Рис. 10.10. Схема потоков вещества по трофическим

пирамидам в замкнутой экосистеме

Система уравнений, описывающая потоки вещества, приведенные на рис. 10.10, имеет вид

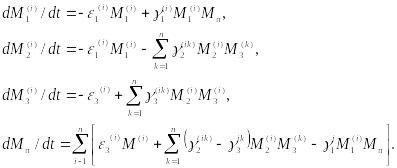(10.16)

Здесь верхние индексы указывают номер трофической пирамиды, а нижние – номер трофического уровня, которому принадлежит соответствующий вид. Все и – положительные числа. и – коэффициенты естественной смертности продуцентов и редуцентов i-й пирамиды, и коэффициенты роста продуцентов и редуцентов i-й пирамиды. Так как прирост биомассы редуцентов происходит только за счет опада от всех п пирамид, константа скорости роста редуцентов не должна превышать константу поступления опада , т.е. должны выполняться соотношения:

.

В системе (10.16) сохраняется общая масса компонентов. Действительно, сложив уравнения (10.16), получим

, т.е.

Обозначим через М массу всего биогеоценоза, будем иметь

Выберем два произвольных уравнения из (10.16), пусть это будет р-е и k-e уравнения. Умножим первое из них на а второе – на вычтем затем из первого уравнения второе:

Обозначим через М массу всего биогеоценоза, будем иметь

Интегрируем и получим

,

где С = const. Пусть теперь

В этом случае . Но величина ограничена сверху значением М. Поэтому , т.е. р-й вид вытесняется k-тым видом, у которого отношение меньше. Условие равновесия видов, т.е. совместного бесконечно долгого существования на одном и том же трофическом уровне, имеет вид

Оно очень жесткое и в природе вряд ли может быть выполнено.

Повторяя аналогичную процедуру для всех пар уровней получим, что в результате конкурентной борьбы между продуцентами и в отсутствие консументов выживает вид s с наименьшим значением отношения коэффициента смертности к коэффициенту роста , независимо от характера связей редуцентов с опадом. В фазовом пространстве, по осям которого отложены биомассы видов, траектории системы будут сходиться к одной устойчивой особой точке, соответствующей состоянию, в котором элиминируются виды всех трофических пирамид, кроме одной, где отношение наименьшее.

Отношение определяется, с одной стороны, свойствами организмов, а с другой – внешними условиями: температурой, влажностью и химическим составом среды. Это позволяет сделать вывод, что, подбирая условия жизни биоценоза так, чтобы отношение было минимальным для интересующего нас вида, мы тем самым создаем условия для устранения нежелательных конкурентов.

Рассмотрение биогеоценоза как замкнутой по веществу системы позволяет дать математическое толкование роли консументов в сообществе. Система со специализированными консументами в отличие от системы без консументов не вырождается в одну трофическую пирамиду: существуют устойчивые стационарные состояния, ненулевые для нескольких видов продуцентов и соответствующих им специализированных консументов. Это объясняется тем, что введение специализированных консументов приводит к ослаблению конкурентного воздействия продуцентов друг на друга, так как соответствующий консумент ограничивает увеличение численности наиболее приспособленного продуцента и препятствует вытеснению остальных видов растений.

Буферная система, состоящая из опада и редуцентов, определяет количество минерализируемого вещества, биомассу и количество пар продуцент – консумент, но не сказывается на взаимодействии между теми парами, для которых в данной системе существует стационарное состояние.

Таким образом, система со специализированными консументами более стабильна, чем без консументов, которая вырождается в конечном итоге в одновидовую систему и оказывается поэтому очень чувствительной к резким изменениям внешних условий. Однако если консументы неспециализированны, например один консумент поедает все продуценты системы, то, как и в случае отсутствия консументов, это приводит с течением времени к одной простой пищевой цепи, которая неустойчива по отношению к резким изменениям внешних условий.

В природе чаще всего наблюдается некоторый промежуточный случай, когда консументы преимущественно питаются одним или несколькими видами растений. Специализация консументов играет ведущую роль в сохранении видового и генетического разнообразия растений, которое обеспечивает устойчивость биоценозов к изменению внешних условий.

В рассмотренных моделях сложных биогеоценозов как замкнутых по массе систем могут существовать не только устойчивые стационарные состояния. В отличие от систем Вольтерра, в моделях систем, замкнутых по массе, не может быть негрубых особых точек типа центр. Зато появляются широкие возможности для существования автоколебательных и триггерных режимов, по-видимому, наиболее соответствующих природным ситуациям.

Еще более осложняется система при учете того факта, что незаменимых компонентов питания, необходимых живым организмам, много. В процессе жизнедеятельности может происходить такое перераспределение вещества в питательной среде, что процесс роста попеременно ограничивается разными биогенами. На примере замкнутой системы из двух видов водорослей и двух лимитирующих биогенов показано, что конкурентные отношения в такой системе достаточно сложные. Например, здесь существует область параметров с колебательным изменением переменных, а также области, имеющие вид двойных и тройных триггеров, причем исход конкуренции зависит от начальных плотностей популяций.

В системах с фиксированным количеством вещества могут возникать также хаотические режимы. Результаты о зарождении таких режимов и их свойствах получены в работах В.В. Алексеева и А.Ю. Лоскутова для 4-видовой системы, состоящей из двух хищников и двух жертв. В более ранних работах В.В. Алексеевым (1976) были предложены модели замкнутых по веществу сообществ, в которых насыщение процессов выражается в форме Моно. Для сообщества из N пар хищник–жертва такая модель запишется в виде

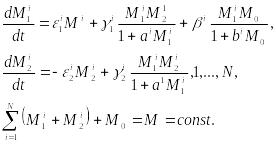(10.19)

Здесь i - номер трофической пирамиды, – биомасса (масса лимитирующего вещества) 1-й жертвы, – биомасса 1-го хищника. Взаимодействие между трофическими парами осуществляется на уровне потребления общего ресурса М_o. В случае двух пар систему можно представить в виде

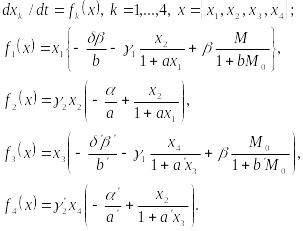(10.20)

Здесь x₁,x₂ – биомассы жертв первой и второй пары, х_з, x₄ – биомассы хищников первой и второй пары,

От рассмотренных выше моделей в обыкновенных дифференциальных уравнениях, имеющих области хаотического поведения, система (10.19-10.20) отличается неполиномиальным заданием правых частей уравнений. Фазовым пространством системы является 4-мерный положительный конус. Показано, что стохастическое движение стационарно и обладает сплошным спектром; в отличие от регулярного движения оно обладает положительной энтропией Колмогорова. Это означает, что система “забывает” начальные условия после первого же оборота в фазовом пространстве.

В моделях типа (10.19) обнаружена следующая последовательность перехода к квазистохастическому режиму: устойчивая особая точка – устойчивый предельный цикл – двухмерный инвариантный тор – хаотичность.

На основании численных расчетов установлено, что хаотическое множество локально имеет вид произведения канторова множества на отрезок. Это фрактальное множество занимает промежуточное положение между гладкой линией и гладкой поверхностью, т.е. его фрактальная размерность дробная. Границы зон динамической стохастичности в пространстве параметров очень изрезаны (рис. 10.11).

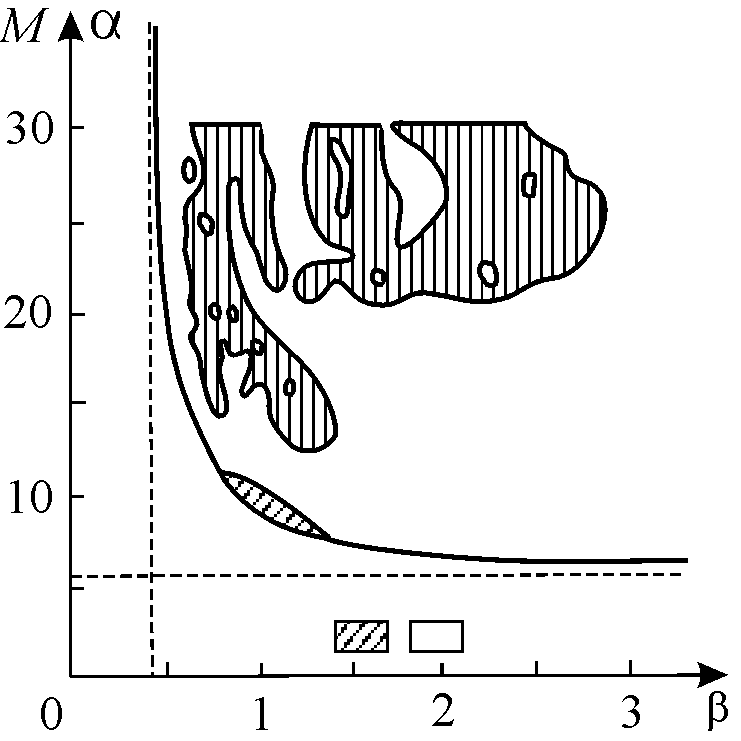
Рис. 10.11. Области стохастичности (штриховка) для системы (10.19):

два хищника – две жертвы. (Алексеев, Лоскутов, 1985)

При наложении шумов на систему (а в реальности такие случайные воздействия на систему всегда присутствуют) границы будут размываться, и общий объем хаотических областей, по-видимому, увеличится. Поэтому при биологической трактовке моделей таких систем не следует придавать большого значения точным величинам параметров на границах областей стохастичности. Гораздо больший интерес представляет вопрос, насколько велик общий объем таких параметрических областей и имеют ли параметры значения, близкие к реальным.

Приложение.

Примеры фрактальных множеств.

Мы говорили о том, что странные аттракторы имеют фрактальную структуру. Относительно определения фрактала до сих пор ведутся споры. Однако, все эти определения включают в себя представление о том, что фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.

Измерение длины, площади, или объема такого типа объектов представляет значительные трудности. Классическим примером фрактальной линии является береговая линия Норвегии. (Е. Феддер. Фракталы, М., Мир, 1991, с. 260).

Для измерения этой изрезанной линии можно воспользоваться штанген-циркулем c раствором δ, и измерять длину в количестве отрезков. Тогда длина береговой линии будет равна произведению числа отрезков на длину одного отрезка L=N(δ)δ. При этом, чем меньше будет раствор циркуля (подробнее измерение), тем больше будет полученная длина.

Другой способ – воспользоваться квадратными ячейками с размером δ х δ, которыми мы будем покрывать эту кривую. Число N(δ) ячеек, необходимых для того, чтобы покрыть береговую линию на карте приближенно равно числу шагов, за которое можно обойти по карте береговую линию с циркулем раствором δ. Однако, чем более подробным будет измерение (меньше площадь одной ячейки), тем меньше будет полученная общая площадь. При уменьшении δ (δ®0) измеренная длина береговой линии не стремится к постоянному значению, как это было бы для обычной гладкой кривой, но хорошо описывается формулой:

(П.1)

Для обычной кривой множитель a равен сумме длин отрезков: a=L_N, а показатель D равен единице. Но для береговой линии Норвегии D ~ 1,52. Показатель D называется размерностью Хаусдорфа-Безиковича или фрактальной размерностью.

По определению основателя науки о фракталах Бенуа Мандельброта, «фракталом называется множество, размерность Хаусдорфа-Безиковича которого строго больше его топологической размерности».

Фракталы можно рассматривать как множества точек, вложенные в пространство. Например, множество точек, образующих линию в обычном евклидовом пространстве (Е=3) имеет топологическую размерность D_τ = 1 и фрактальную размерность D = 1. Линия, согласно определению Мандельброта, не фрактальна. Аналогично, множество точек, образующих поверхность в евклидовом пространстве, имеет топологическую размерность D_τ = 2 и фрактальную размерность D = 2. Обычная поверхность не фрактальна независимо от того, насколько она сложна. Однако существуют множества, для которых топологическая и фрактальная размерность не совпадают. Это имеет место в случае, когда при последовательном уменьшении измеряющего элемента, длина кривой не стремится к определенному пределу. Например, существуют кривые, закрученные так сильно, что длина их окажется бесконечной, или поверхности, изогнутые столь причудливым образом, что они занимают все пространство.

Фрактальная размерность D кривых, подобных береговой линии, заключена в интервале от 1 до 2, фрактальная размерность существенно пространственных объектов – облаков – от 2 до 3.

Вот некоторые примеры фрактальных множеств, предложенных математиками.