Размерности аттракторов

Важной отличительной чертой странного аттрактора является его сложная геометрическая структура. Характеристикой геометрической структуры является размерность, которая зависит от метрических свойств аттрактора. Такую размерность называют фрактальной размерностью.

Размерность, определяемую с учетом вероятности посещения траекторией различных областей аттрактора в фазовом пространстве, называют информационной. Она зависит от статистических свойств потока, определяемого динамикой системы и может быть оценена из спектра Ляпуновских показателей.

Введем определение фрактальной размерности D_F произвольного предельного множества G в N-мерном фазовом пространстве по Колмогорову‑Хаусдорфу:

(10.13)

Здесь М – минимальное число N–мерных кубиков со стороной e, необходимых для покрытия всех элементов множества G.

Если это определение применить для вычисления размерности точки, линии и поверхности, мы получим привычные для нас величины 0, 1, 2. Для геометрически сложных множеств размерность (10.13) может оказаться дробной.

Примером множества дробной размерности является канторовское множество, описанное в приложении 10.1.

Вычисленная по формуле (10.13) размерность канторовского множества

Мы уже видели на примере преобразования подковы Смейла, что странные аттракторы имеют структуру типа канторовской.

Информационная размерность D_I определяется следующим образом:

(10.14)

Здесь I(e) – количество информации, необходимое для того, чтобы определить состояние системы в пределах точности e, М(e) – число кубиков, со стороной e, покрывающих аттрактор, Р_i – вероятность посещения фазовой траекторией i-го кубика. Поскольку для малых , размерность D_I характеризует скорость возрастания информации с уменьшением e.

Существует также понятие ляпуновской размерности, которая позволяет выразить величину размерности через значения характеристических ляпуновских показателей.

После определения характерных свойств и разработки методов диагностики явления детерминированного хаоса, оно было обнаружено практически во всех областях науки. Мы рассмотрим некоторые примеры моделей квазистохастического поведения биологических систем.

Стационарные состояния и динамические режимы в сообществе из трех видов

Для системы из трех видов в случае разветвленной трофической цепи даже исследование автономной локальной системы становится чрезвычайно сложным. Здесь отступление от вольтерровской схемы и учет биологических факторов, влияющих на динамику численности сосуществующих популяций, приводят к большому разнообразию модельных систем.

В работах А.Д. Базыкина, А.И. Хибника, Т.И. Буриева (1985) проведено качественное исследование систем, состоящих из трех видов, и получены полные наборы двухмерных срезов параметрического портрета и фазовых портретов для сообществ два хищника–жертва и две жертвы–хищник. При исследовании последней системы получены результаты, свидетельствующие о стабилизирующей роли хищника в таком биоценозе. Если в отсутствие хищника, в соответствии с теорией Гаузе, сосуществование двух видов жертв невозможно, то при наличии хищника в системе при разных значениях параметров возможны следующие разнообразные режимы (Базыкин, 1985).

1. Глобально притягивающие режимы: а) одна популяция без хищника; б) одна популяция жертвы с хищником; в) стационарное сосуществование трех популяций.

2. Триггерные режимы:

а) в отсутствие хищника либо одна, либо другая популяция жертвы;

б) либо одна популяция жертвы сосуществует с хищником, либо другая существует без хищника;

в) с хищником сосуществует либо одна, либо другая популяция жертвы;

г) устойчивое стационарное сосуществование всех трех популяций либо существование одной из популяций жертвы в отсутствие хищника и конкурента;

д) то же, но сосуществование всех трех видов возможно лишь в автоколебательном режиме.

Отсюда следуют интересные результаты, касающиеся условий сосуществования популяций.

1. Введение в сообщество хищника может обеспечить устойчивое сосуществование конкурирующих видов жертвы, невозможное в отсутствие хищника. Сходный результат был получен В.В. Алексеевым (1976) при анализе систем с ограничением по массе.

2. Режим сосуществования всех трех популяций может быть либо глобально устойчивым, либо иметь в фазовом пространстве границу области притяжения (триггерность).

3. Сосуществование всех трех видов может происходить в стационарном или автоколебательном режиме в отсутствие каких-либо специальных дестабилизирующих факторов (в силу автономных свойств системы).

В системах, состоящих из хищника и двух жертв при наличии внутривидовой конкуренции между жертвами при изменении параметров системы, возможны бифуркационные явления, приводящие к появлению квазистохастических режимов.

Примером такой системы, обладающей различными типами поведения в зависимости от соотношения параметров, является рассмотренная А.Д. Базыкиным с сотрудниками модель хищник — две жертвы:

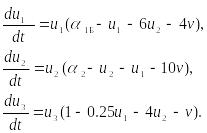(10.15)

Здесь u₁, u₂ - безразмерные численности жертв, v - безразмерная численность хищников, a₁, a₂ - параметры, соответствующие скоростям роста численностей жертв.

В такой системе наряду с устойчивым состояния равновесия возможны колебательные изменения численностей всех трех видов. В некоторой области параметров в системе имеется предельный цикл сложной формы.

При уменьшении a₂ наблюдается серия последовательных удвоений цикла (рис. 10.8 а-в). В некотором диапазоне значений a₂, из результатов численного эксперимента видно, что траектория системы полностью заполняет некоторый фазовый объем. При этих значениях параметров поведение системы неотличимо от случайного, т.е. является квазистахостическим (рис. 10.8 г). Притягивающая область в фазовом пространстве является странным аттрактором.

Модельному режиму, изображенному на рис. 10.8 г соответствуют наблюдаемые в природе нерегулярные квазистохастические изменения численностей животных.