Линейный анализ устойчивости траекторий.

Линейный анализ устойчивости траекторий проводится подобно тому, как мы проводили линейный анализ устойчивости стационарных состояний в лекции 4. Поскольку мы анализируем малое возмущение, можно линеаризовать оператор эволюции в окрестности исследуемой траектории и провести линейный анализ ее устойчивости.

Для автономной динамической системы

x – вектор переменных, a - вектор параметров, F – вектор-функция с компонентами f_j.

Нас интересует устойчивость решения x⁰(t)

Введем малое возмущение y = x(t) – x⁰(t). Для него можно записать

Раскладывая F(x⁰ +y) в ряд в окрестности x⁰ и учитывая малость возмущения, получим линеаризованное уравнение относительно y:

(10.4)

где А – матрица линеаризации системы с элементами

Матрица А характеризуется собственными векторами е_i и собственными значениями r_i:

Ae_i = r_ie_i , i=1,2,…,N. (10.5)

Собственные числа являются корнями характеристического уравнения

, (10.6)

где Е – единичная матрица.

Начальное возмущение с течением времени будет меняться в соответствии с эволюцией вектора

. (10.7)

Будет отклонение уменьшаться или нарастать, определяется значением действительной части r_i.

Элементы матрицы А со временем могут меняться. Соответственно меняются ее собственные вектора и собственные значения, в том числе может меняться знак действительной части r_i. Необходимо понять, что происходит с возмущением в пределе при t ® ¥.

Для общей характеристики устойчивости траектории по отношению к возмущению вдоль i-го собственного вектора используют величину, называемую характеристическим показателем Ляпунова:

(10.8)

Для N-мерной задачи устойчивость траектории характеризуется набором N Ляпуновских характеристических показателей. Они связаны с собственными значениями матрицы линеаризации соотношением:

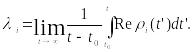(10.9)

Таким образом, ляпуновский показатель – это усредненное вдоль исследуемой траектории значение действительной части собственного значения r_i матрицы линеаризации.

Устойчивость траектории по Ляпунову означает, что произвольное начальное возмущение y(t₀) в среднем вдоль траектории не возрастает. Для этого необходимо и достаточно, чтобы спектр ляпуновских показателей l_i не содержал положительных показателей.

Диссипативные системы.

В физике системы принято подразделять на консервативные и диссипативные. В консервативных системах энергия сохраняется (маятник без затухания). В диссипативных системах энергия со временем уменьшается (маятник в вязкой среде). Для того чтобы диссипативная система поддерживала непрерывное движение (например, автоколебания), необходимы источники энергии.

Биологические системы по своей природе являются диссипативными. Поэтому их модели принципиально нелинейны. Существование аттрактора в диссипативной системе связано со свойством сжатия элемента фазового объема под действием оператора эволюции. Рассмотрим множество точек, заполняющих элемент объема DV, и множество фазовых траекторий, стартующих из этих точек в момент времени t₀ (рис. 10.4).

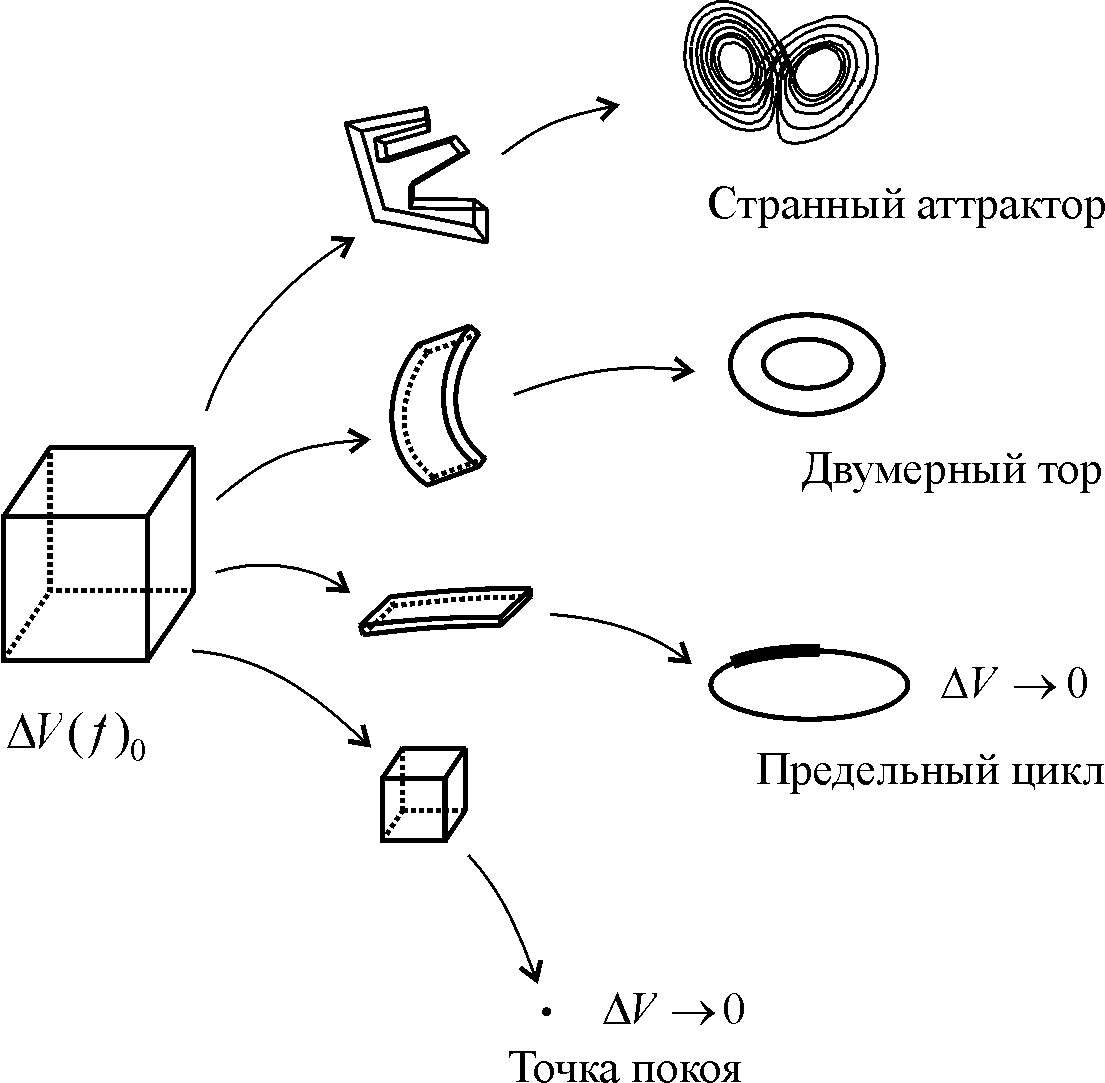
Рис. 10.4. Сжатие элемента фазового объема в разные типы аттракторов

С течением времени объем DV меняется по закону:

,

где F(x(t)) – поле фазовых скоростей (поток) динамической системы. Черта сверху означает усреднение вдоль фазовой траектории. Если в среднем дивергенция потока отрицательна, а это всегда выполняется для систем с потерями, то элемент фазового объема DV в пределе при t ® ¥, стремится к нулю. Это означает, что рассматриваемое множество фазовых траекторий, которые берут свое начало в DV, стремится попасть на некоторое предельное множество, размерность которого меньше размерности N фазового пространства системы.

На рис. 4.10 нарисованы различные типы аттракторов, в которые может перейти элемент фазового пространства размерности 3. Это – точка покоя (1), предельный цикл (2), двумерная поверхность, диффеоморфная поверхности тора (3), и, наконец, хаотический аттрактор (4).

Средняя вдоль траектории дивергенция потока и, следовательно, эволюция элемента фазового объема, определяется суммой ляпуновских показателей

(10.10)

Для фазовых траекторий на аттракторе должно иметь место сжатие элемента фазового объема. Соответственно, дивергенция потока вдоль траектории отрицательна, а значит, ляпуновские показатели удовлетворяют неравенству

(10.11)

Хаотические аттракторы имеют по крайней мере один положительный ляпуновский показатель. Если траектории на аттракторе имеют более, чем одно направление неустойчивости, хаос называется гиперхаосом.