Лекция 10

ДИНАМИЧЕСКИЙ ХАОС. МОДЕЛИ БИОЛОГИЧЕСКИХ СООБЩЕСТВ

Основные понятия теории динамических систем. Предельные множества. Аттракторы. Странные аттракторы. Динамический хаос. Линейный анализ устойчивости траекторий. Диссипативные системы. Устойчивость хаотических решений. Размерность странных аттракторов.

Стационарные состояния и динамические режимы в сообществе из трех видов. Трофические системы с фиксированным количеством вещества. Модель четырехвидовой системы.

Мы рассмотрели модели систем, которые описываются с помощью двух дифференциальных уравнений, их поведение можно наглядно изобразить на фазовой плоскости. Для таких двумерных систем в рамках качественной теории дифференциальных уравнений разработана исчерпывающая теория возможных типов динамического поведения. Применение этой теории к моделям двух взаимодействующих видов мы рассмотрели в лекции 9.

Когда встает вопрос описания сложных многокомпонентных систем, например, биологических сообществ, необходимо использовать системы большей размерности. Здесь полной классификации типов динамического поведения не существует. Известно, что увеличение размерности позволяет описать качественно новые типы поведения. Так, одно автономное уравнение может описать лишь монотонные изменения переменной. Система двух автономных уравнений может иметь более сложные типы поведения – предельные циклы, множественные стационарные состояния.

Во второй половине 20 века стало понятно, что в автономной системе третьего и более высокого порядка возможны квазистохастические режимы. Впервые этот вывод для некоторых механических систем сделал еще на грани 19‑20 веков французский математик Анри Пуанкаре. В книге «Наука и метод» в 1908 г. он писал: «В неустойчивых системах совершенно ничтожная причина, ускользающая от нас по своей малости, вызывает значительные действия, которые мы не в состоянии предугадать… Предсказание становится невозможным, мы имеет перед собой явление случайное».

Однако большинством физиков этот результат был воспринят как курьез, и прошло более 70 лет, пока метеоролог Лоренц (Lorenz, 1963) не обнаружил, что даже простая система из трех нелинейных дифференциальных уравнений

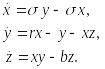(10.1)

может привести к хаотическим траекториям (рис.10.1).

Рис.10.1. Хаотические траектории в системе Лоренца

В последующие десятилетия значимость работы Лоренца стала общепризнанной. Он открыл один из первых примеров детерминированного хаоса в диссипативных системах. Хаотическое поведение затем было обнаружено при расширении их размерности в большинстве классических моделей биологических систем, имеющих колебательные решения, в том числе в моделях взаимодействия видов, моделях гликолиза и клеточного цикла, моделях ферментативного катализа и других. Некоторые из этих моделей мы рассмотрим в дальнейшем.

Хаотическое поведение в таких системах возникает

1. не из-за внешних источников шума (их нет в системе Лоренца);

2. не из-за бесконечного количества степеней свободы (их три в системе Лоренца);

3. не из-за неопределенности, связанной с квантовой механикой (рассматриваемые системы чисто классические).

Настоящая причина нерегулярности определяется свойством нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства. Механической системой такого типа является биллиард Синая, у которого стенки выпуклы внутрь, отчего угол отражения шара от стенки приводит к большому (экспоненциальному) разбеганию траекторий при малых отклонениях угла падения. То же происходит при рассеивании частиц на круглых шарах. В таких системах траектория частицы становится непредсказуемой на больших временах.

К такому типу процессов относятся жидкости вблизи порога возникновения турбулентности, приборы нелинейной оптики (лазеры), некоторые химические реакции, метеорологические процессы, движения горных масс при землетрясениях. К ним относятся и многие биологические процессы в достаточно узкой области значений параметров. Изучение роли динамического хаоса в организации биологических процессов – одна из актуальных задач математической биологии.

Необходимым (но не достаточным) условием существования динамического (детерминированного) хаоса является нелинейность. Линейные дифференциальные и разностные уравнения могут быть решены преобразованием Фурье и не приводят к хаосу.

Понятие «хаотическое поведение» означает неустойчивость фазовых траекторий, рост малого начального возмущения во времени, перемешивание элементов фазового объема, и, как следствие, непредсказуемость поведения системы на больших временах.

Важно, что такого типа режимы обнаруживаются в детерминированных системах, где однозначно задан закон изменения системы с течением времени. Детерминированность означает, что зависимость будущего состояния x (t) можно записать в виде:

x(t) = F [x(t₀)] . (10.2)

Здесь F – детерминированный закон (оператор), который осуществляет строго однозначное преобразование начального состояния x(t₀) в будущее состояние x(t) для любого t > t₀. Частный случай такого закона мы видели в лекции 3, когда изучали дискретный аналог логистического уравнения. При некоторых значениях параметра эта система демонстрировала квазистохастическое поведение. Мы видели, что траектории системы при этом приобретали сложный непериодический характер. И попытки воспроизвести начальную реализацию приводили к непредсказуемым результатам. Как в случае истинно хаотического броуновского движения, с каждой новой реализации при тех же начальных условиях (в пределах возможной точности!) мы получали другие сложные траектории, даже близко не напоминающие друг друга. На самом деле, если бы начальные значения воспроизводились с абсолютной точностью, сложная траектория также бы повторилась. Но в области детерминированного хаоса траектории являются неустойчивыми по отношению к малым отклонениям. Поэтому даже малейшие отклонения, допускаемые компьютером, приводят к разбеганию.

Этим и объясняется название «детерминированный хаос», объединяющее два несовместимых представления – детерминированность (однозначную определенность) и непредсказуемость поведения.

Для понимания свойств детерминированного хаоса вернемся к определению основных понятий теории динамических систем.

Устойчивость и неустойчивость.

В лекциях 2,4 мы рассмотрели понятие устойчивости стационарного состояния по Ляпунову. Однако устойчивостью и неустойчивостью характеризуются не только состояния равновесия, но любые фазовые траектории. Существует несколько понятий устойчивости движения: устойчивость по Ляпунову, асимптотическая устойчивость, орбитальная устойчивость, устойчивость по Пуассону.

Для устойчивого по Ляпунову движения малое начальное возмущение не нарастает. Т.е. движение устойчиво по Ляпунову, если для любого e > 0 можно указать такое d (e), что для всякого движения x(t), для которого êêx(t)-x*(t) êê< d, при всех t > t₀ выполняется неравенство êêx(t)-x*(t)êê< e.

Знак êê êêозначает норму вектора.

Если малое начальное возмущение d не только не нарастает, а со временем стремится к нулю, то есть êx(t)-x*(t) ê ® 0 при t ® ¥ то движение обладает более сильным свойством асимптотической устойчивости.

В понятии орбитальной устойчивости рассматривается не расстояние между точками исходной и возмущенной траекторий в один и тот же момент времени, а минимальное расстояние от изображающей точки возмущенной траектории до орбиты Г*, соответствующей исходному движению. Орбитально устойчивое движение может не быть устойчивым по Ляпунову.

Устойчивость движения по Пуассону предполагает, что соответствующая фазовая траектория при t ® ¥ не покидает ограниченной области фазового пространства. Находясь в этой области бесконечно долго, она неизбежно будет возвращаться в сколь угодно малую окрестность начальной точки. Времена возврата могут соответствовать периоду или квазипериоду при регулярном движении, а могут представлять собой случайную последовательность, если решение отвечает режиму динамического хаоса.

Предельные множества.

Понятие предельного множества играет важнейшую роль в нелинейной динамике. Изучая некоторые модели биологических систем, мы уже сталкивались с несколькими типами предельных множеств. В первую очередь, с устойчивыми стационарными состояниями типа устойчивый узел и фокус, а также с устойчивыми замкнутыми фазовыми траекториями – предельными циклами (лекция 8). В динамических системах третьего порядка кроме этих двух типов возможны тороидальные предельные множества, соответствующие квазипериодическим фазовым траекториям, и еще более сложные хаотические предельные множества.

Пусть в момент времени t₀ состояние системы определяется вектором x_0, а в момент t – вектором x(t) = T_Dt x₀, где T_Dt – оператор эволюции на интервале Dt = t - t₀. Если в фазовом пространстве существуют два множества V и L Î V, такие, что для любого начального состояния x₀ÎV при t ® ¥ или при t ® -¥, начиная с определенного момента времени x(t)ÎL, то тогда L называют предельным множеством динамической системы.

Таким образом под действием оператора эволюции все точки системы в пределе переходят в точки предельного множества.

Если все точки множества V будут принадлежать L при t ® +¥, то L – притягивающее предельное множество, или аттрактор. Тогда V – бассейн притяжения аттрактора (подобно бассейну реки – территории, с которой она собирает свои воды).

Если все точки множества V будут принадлежать L при t ® -¥, то L – отталкивающее предельное множество, или репеллер.

Если множество V состоит из двух подмножеств V = W^s È W^u, причем точки, принадлежащие W^s, стремятся к L в прямом времени, а точки, принадлежащие W^u, стремятся к L в обратном времени, тогда L называется седловым предельным множеством (или седлом). Множества W^s и W^u - устойчивое и неустойчивое многообразия седла. При инверсии времени (такую возможность предоставляют большинство современных математических пакетов для визуального решения дифференциальных уравнений) аттракторы системы становятся репеллерами, репеллеры – аттракторами, а у седел меняются ролями устойчивое и неустойчивое многообразия.

Мы знакомы с простейшими предельными множествами динамической системы – состояниями равновесия (лекция 4). Устойчивый узел и устойчивый фокус являются аттракторами, неустойчивый узел и неустойчивый фокус – репеллерами. Седлами являются простое седло, рассмотренное в лекции 4, и седло-фокус, реализуемый в фазовом пространстве с размерностью N ³ 3 (рис. 10.2).

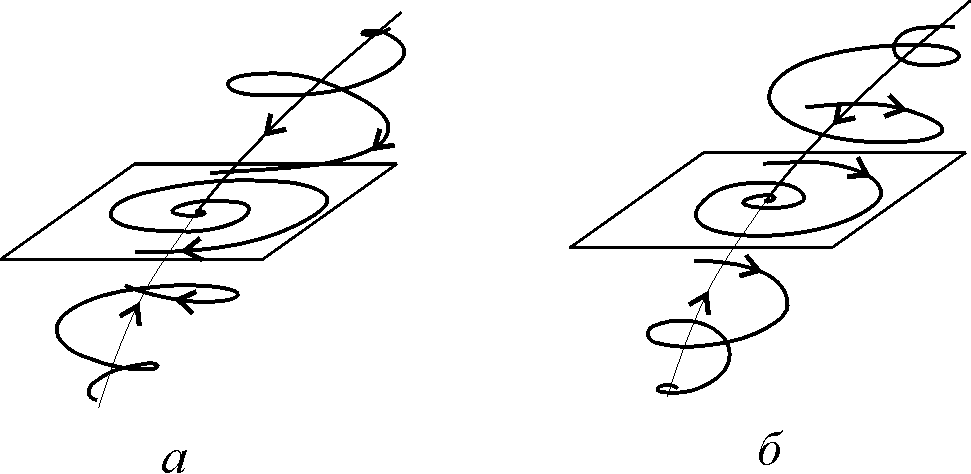
Рис. 10.2. Седло-фокусы в пространстве N = 3.

a) р₁ - действительно и отрицательно, р_2,3 – комплексно сопряженные, Re р_2,3 > 0; б) р₁ - действительно и положительно, р_2,3 – комплексно сопряженные, Re  р_2,3 < 0

Точка типа «центр», которую мы рассматривали в простейшей вольтерровской системе «хищник-жертва» (лекция 5) не является ни аттрактором, ни репеллером, ни седлом, так как не существует множества точек, стремящихся к центру в прямом или обратном времени. Это особый случай предельного множества, для которого V = L. Такая особая точка является негрубой.

Предельное множество в виде замкнутой кривой также может быть аттрактором – устойчивый предельный цикл, репеллером - неустойчивый (см. лекция 8). Седловые предельные циклы существуют лишь в фазовом пространстве размерности N ³ 3.

Таким же образом подразделяются тороидальные предельные множества, соответствующие квазипериодическим колебаниям с двумя несоизмеримыми частотами. Седловые торы существуют в пространстве N ³ 4.

Все перечисленные предельные множества представляют собой простые в геометрическом смысле множества - точка, кривая, поверхность – целой размерности (0, 1, 2). Их называют регулярными. Отметим, что с увеличением размерности фазового пространства старые типы предельных множеств, присущие пространствам малой размерности, сохраняются, и появляются новые.

В системах с размерностью фазового пространства N ³ 3 возможны установившиеся изменения переменных, не являющиеся ни периодическими, ни квазипериодическими. Таким хаотическим изменениям переменных соответствуют аттракторы, представляющие собой геометрически сложные множества дробной размерности, названные «хаотическими аттракторами». Пример одной из классических систем, демонстрирующих детерминированный хаос, представляет система Ресслера:

(10.3)

Траектории системы (10.3) напоминают клубок спутанных ниток (рис.10.3).

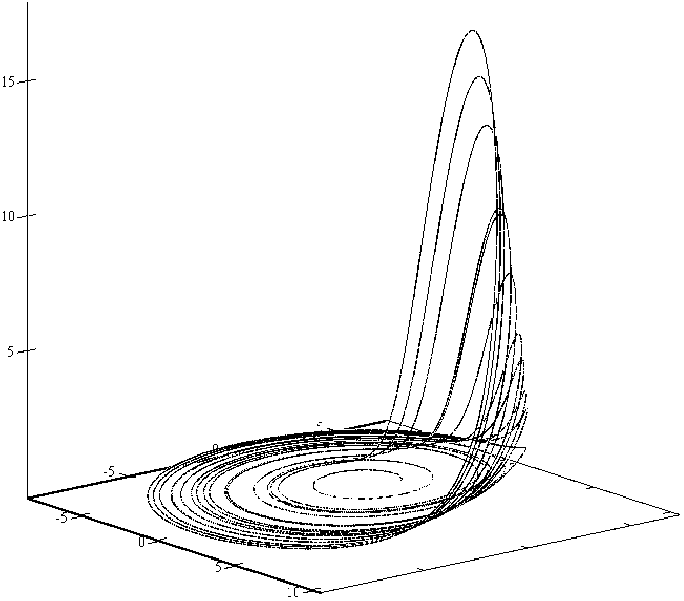
Рис.10.3. Вид проекций фазовой траектории на странном аттракторе в системе Ресслера.