4.Нормальный закон распределения и его значение для прикладной статистики.
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности.
Нормальный закон распределения также называется законом Гаусса
распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
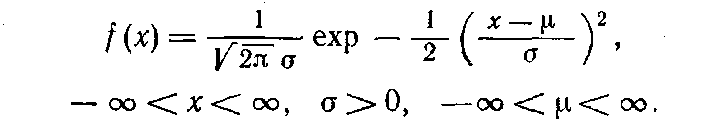
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистике. Физическая величина, подверженная влиянию значительного числа независимых факторов, могущих вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Свойства
Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиями и соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией .
Моделирование нормальных случайных величин
Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.
Центральная предельная теорема
Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
отклонение при стрельбе, погрешности измерений, рост живых организмов
Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).
Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием центральной предельной теоремы.
6.Непараметрические критерии однородности двух выборок.
Непараметрические критерии
Для преодоления указанных трудностей в практике исследований следует использовать непараметрические критерии статистики, такие, как критерий знаков, двухвыборочный критерий Вилкоксона, критерий Ван дер Вардена, критерий Спирмена, выбор которых, хотя и не требует большого числа членов выборки и знаний, вида распределения, но все же зависит от целого ряда условий.
Непараметрические критерии статистики - свободны от допущения о законе распределения выборок и базируются на предположении о независимости наблюдений. непараметрические критерии: критерий знаков и критерий хи-квадрат.
Критерий знаков (G-критерий)
Критерий предназначен для сравнения состояния некоторого свойства у членов двух зависимых выборок на основе измерений, сделанных по шкале не ниже ранговой.
Имеется две серии наблюдений над случайными переменными X и У, полученные при рассмотрении двух зависимых выборок. На их основе составлено N пар вида (хi, уi), где хi, уi — результаты двукратного измерения одного и того же свойства у одного и того же объекта.Элементы каждой пары хi, уi сравниваются между собой по величине, и паре присваивается знак «+», если хi < уi , знак «—», если хi > уi и «0», если хi = уi.
Нулевая гипотеза формулируются следующим образом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно различны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.
Статистика критерия (Т) определяется следующим образом: допустим, что из N пар (х, у,) нашлось несколько пар, в которых значения хi и уi равны. Такие пары обозначаются знаком «0» и при подсчете значения величины Т не учитываются. Предположим, что за вычетом из числа N числа пар, обозначенных знаком «0», осталось всего n пар. Среди оставшихся n пар подсчитаем число пар, обозначенных знаком «-», т.е, пары, в которых xi<yi. Значение величины Т и равно числу пар со знаком минус.
Следовательно, верно неравенство Т<n—ta (15<16).
Критерий χ2 (хи-квадрат)
Критерий χ2 (хи-квадрат) применяется для сравнения распределений объектов двух совокупностей на основе измерений по шкале наименований в двух независимых выборках
Критерий не рекомендуется использовать, если:
1) сумма объемов двух выборок меньше 20;
2) хотя бы одна из абсолютных частот в таблице 2X2, составленной на основе экспериментальных данных, меньше 5.
Назначения критерия
Критерий χ2 применяется в двух целях;
1) для сопоставления эмпирического распределения признака с теоретическим - равномерным, нормальным или каким-то иным;
2) для сопоставления двух, трех или более эмпирических распределений одного и того же признака1.
Описание критерия
Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.
Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтернативного распределения "да - нет", "допустил брак - не допустил брака", "решил задачу - не решил задачу" и т. п. мы уже можем применить критерий χ2.